Лекция
Привет, Вы узнаете о том , что такое доказательство, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое доказательство, опровержение, доказательство в широком смысле , настоятельно рекомендую прочитать все из категории Логика.
Невозможно переоценить значение доказательств в нашей жизни и особенно в науке. И, тем не менее, доказательства встречаются не так часто, как хотелось бы. Иногда за доказательство выдается то, что им вовсе не является. К доказательствам прибегают все, но редко кто задумывается над тем, что означает «доказать», почему доказательство «доказывает», всякое ли утверждение можно доказать или опровергнуть, все ли нужно доказывать и т.п.
Доказательство — рассуждение по определенным логическим правилам, обосновывающее истинность какого-либо предположения, утверждения, гипотезы или теории. В разных областях науки, искусства и иной человеческой деятельности этот термин может принимать различные значения.
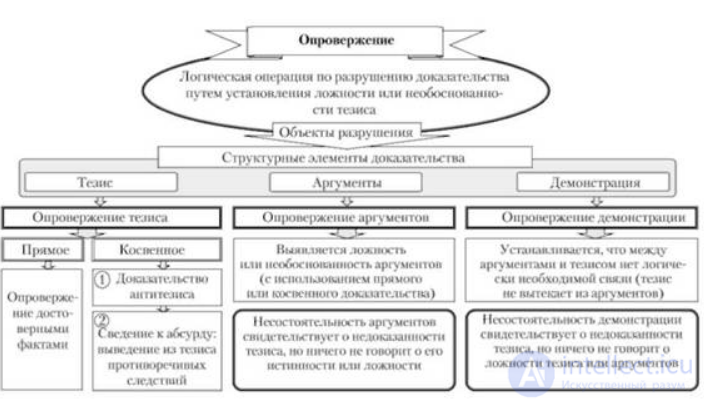
опровержение — это логическая операция, направленная на разрушение доказательства путем установления ложности или необоснованности ранее выдвинутого суждения-тезиса. Это суждение, которое надо опровергнуть, называется тезисом опровержения.
Наше представление о доказательстве как особой интеллектуальной операции формируется в процессе проведения конкретных доказательств. Изучая разные области знания, мы усваиваем и относящиеся к ним доказательства. На этой основе мы постепенно составляем — чаще всего незаметно для себя — общее интуитивное представление о доказательстве как таковом, его общей структуре, не зависящей от конкретного материала, о целях и смысле доказательства и т.д.
Особую роль при этом играет изучение математики. С незапамятных времен математические рассуждения считаются общепризнанным эталоном доказательства. Желая похвалить чью-либо аргументацию, мы называем се математически строгой и безупречной.
Изучение доказательства на конкретных его образцах и интересно, и полезно. Но также необходимо знакомство с основами логической теории доказательства, которая говорит о доказательствах безотносительно к области их применения. Практические навыки доказательства и интуитивное представление о нем достаточны для многих целей, но далеко не для всех. Практика и здесь, как обычно, нуждается в теории.
Логическая теория доказательства в основе своей проста и доступна, хотя ее детализация требует специального символического языка и другой изощренной техники современной логики.
Под доказательством в логике понимается процедура установления истинности некоторого утверждения путем приведения других утверждений, истинность которых уже известна и из которых с необходимостью вытекает первое.
В доказательстве различаются тезис — утверждение, которое нужно доказать, основание(аргументы) — те положения, с помощью которых доказывается тезис, и логическая связь между аргументами и тезисом. Понятие доказательства всегда предполагает, таким образом, указание посылок, на которые опирается тезис, тех логических правил, по которым осуществляются преобразования утверждений в ходе доказательства. В обычной практике мы редко формулируем все используемые посылки и, в сущности, никогда не обращаем внимания на применяемые нами правила логики.
Одна из основных задач логики состоит в придании точного значения понятию доказательства. Но хотя это понятие является едва ли не главным в логике, оно не имеет точного, строго универсального определения, применимого во всех случаях и в любых научных теориях.
«Понятие доказательства, — пишет логик и математик В. А. Успенский, — во всей его полноте принадлежит математике не более чем психологии: ведь доказательство — это просто рассуждение, убеждающее нас настолько, что с его помощью мы готовы убеждать других».
Доказательство — один из многих способов убеждения. В науке это один из основных методов. Можно сказать, что научный метод убеждения является, прежде всего, методом строгих и точных доказательств. Требование доказательности научного рассуждения определяет то «общее освещение», которое модифицирует попавшие в сферу его действия цвета. Этим «общим освещением» пронизываются все другие требования к научной аргументации. Без него она неизбежно вырождается в бездоказательный набор общих деклараций и поучений, в апелляцию к вере и эмоциям.
На каждом из нас лежит «бремя доказательства» выдвигаемых положений. Важно постоянно думать о содержательной стороне дела. Вместе с тем существенно также, чтобы всегда обеспечивалось единство содержательности и доказательности. Никакие искусственные приемы, никакое красноречие не способны помочь, если нет хорошо обоснованных идей и убедительных доказательств.
Задача доказательства — исчерпывающе утвердить обоснованность доказываемого тезиса.
Раз в доказательстве речь идет о полном подтверждении, связь между аргументами и тезисом должна носить дедуктивный характер. По своей форме доказательство — дедуктивное умозаключениеили цепочка таких умозаключений, ведущих от истинных посылок к доказываемому положению.
Старая латинская пословица говорит: «Доказательства ценятся но качеству, а не по количеству». В самом деле, дедукция из истины дает только истину. Если найдены верные аргументы и из них дедуктивно выведено доказываемое положение, доказательство состоялось, и ничего более не требуется.
Нередко в понятие доказательства вкладывается более широкий смысл. При этом под доказательством понимается любая процедура обоснования истинности тезиса, включающая как дедукцию, так и индуктивное рассуждение, ссылки на связь доказываемого положения с фактами, наблюдениями и т.д. Расширительное истолкование доказательства является обычным в гуманитарных науках. Оно встречается и в экспериментальных, опирающихся на наблюдения рассуждениях.
Как правило, широко понимается доказательство и в обычной жизни. Для подтверждения выдвинутой идеи активно привлекаются факты, типичные в определенном отношении явления и т.п. Дедукции в этом случае, конечно, нет, речь может идти только об индукции. Но, тем не менее, предполагаемое обоснование нередко называют доказательством.
Широкое употребление понятия «доказательство» само по себе не ведет к недоразумениям. Но только при одном условии. Нужно постоянно иметь в виду, что индуктивное обобщение, переход от частных фактов к общим заключениям дает не достоверное, а лишь вероятное знание.
Многие наши утверждения не являются ни истинными, ни ложными. Оценки, правила, советы, требования, предостережения не описывают рассматриваемую ситуацию. Они указывают, какой она должна стать, в каком направлении ее надо преобразовать. От описаний мы вправе требовать, чтобы они являлись истинными. Но удачный приказ, совет, и т.д. мы характеризуем как эффективный, целесообразный, но не как истинный.
В стандартном определении доказательства используется понятие истины. Доказать некоторый тезис — значит логически вывести его из других являющихся истинными положений. Но есть утверждения, не связанные с истиной. Очевидно также, что, оперируя ими, можно и нужно быть и логичным, и доказательным.
Возникает, таким образом, вопрос о существенном расширении понятия доказательства. Им должны охватываться не только описания, но и утверждения типа оценок, требований.
Задача переопределения доказательства успешно решается современной логикой. Такие ее разделы, как логика оценок и логика норм, убедительно показывают, что рассуждения о ценностях и нормах также подчиняются требованиям логики и не выходят за сферу логического.
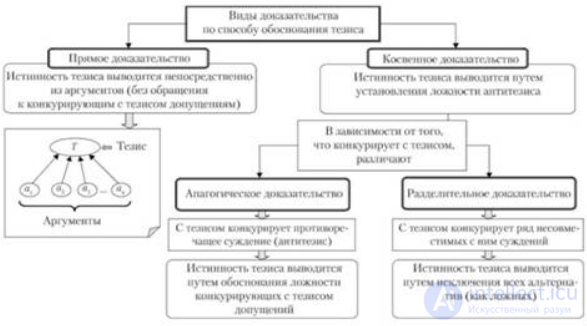
Виды доказательств
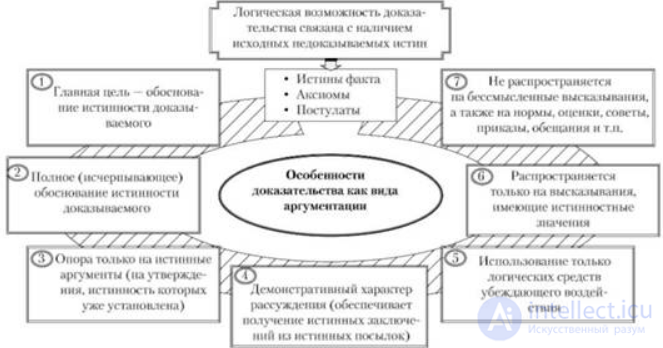
Рис. Об этом говорит сайт https://intellect.icu . . Особенности доказательства как вида аргументации
Способ связи аргументов от условия к заключению суждения называют методом доказательства. Методы доказательства делят на прямые и косвенные. Различают приемы прямого доказательства: прием преобразования условия суждения (синтетический); прием преобразования заключения суждения (восходящий анализ); отыскание необходимых признаков справедливости суждения с последующей проверкой обратимости рассуждений (нисходящий анализ); прием последовательного преобразования то условия, то заключения суждения.
Условие всякой теоремы является достаточным условием по отношению к заключению. В свою очередь заключение – это необходимое условие по отношению к условию этой теоремы.
К приемам косвенного доказательства относят:
1) метод доказательства от противного (истинность доказываемого утверждения устанавливается посредством опровержении противоречащего ему суждения);
2) разделительный (доказываемое утверждение рассматривается как один из возможных вариантов предложений, когда все предположения отвергаются, кроме одного).
Доказательство математического утверждения называется синтетическим, если оно осуществляется по следующей логической схеме:
P1(x)→P2(x)→P3(x)→…Pn-1(x)→Pn(x) = P(x),
где Pi – определенная совокупность предложений той математической теории, в рамках которой доказывается данное утверждение. Таким образом, при синтетическом методе доказательства теоремы цепочка силлогизмов строится так, что мысль движется от условия теоремы к ее заключению.
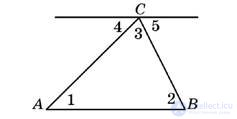
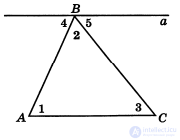
Пример. Рассмотрим синтетическое доказательство теоремы «о сумме внутренних углов треугольника.»
Дано: АВС – треугольник
Доказать:
∟1+∟2+∟3=180°
Доказательство:
1. «Рассмотрим треугольник АВС»
2. «Проведем через вершину В прямую, а, параллельную АВ.»
3. «Рассмотрим ∟1 и ∟4, как эти углы называются?»
«Правильно, они являются накрест лежащими углами при пересечении параллельных прямых а и АС и секущей АВ, а значит, ∟1=∟4.»
4. «Теперь рассмотрим ∟3 и ∟5, что вы можете о них сказать?»
«Правильно, они накрест лежащие при пересечении параллельных прямых, а и АС и секущей ВС, а значит, ∟3=∟5.»
5. «Посмотрите на углы 3,4 и 5, что можно про них сказать»
«Правильно, они образуют развернутый угол»
«Мы уже знаем, что сумма развернутого угла равно 180°, ∟4+∟3+∟5= 180°.»
6. «А так как ∟1=∟4, а ∟3=∟5,мы можем переписать наше выражение как ∟1+∟2+∟3=180°»
7. «Мы доказали, что сумма внутренних углов в треугольнике равна 180°»
При аналитическом доказательстве теоремы цепочка силлогизмов строится так, что мысль движется от заключения теоремы к ее условию. Различают два вида аналитического метода: восходящий анализ (анализ Паппа), нисходящий анализ (анализ Евклида).
Восходящим анализом (совершенным анализом) называется такая разновидность аналитического метода, при котором, отталкиваясь от заключения P(x), подбирают для него достаточное условие – такое суждение
P1(x), что P1(x)→P(x),затем подбирают достаточное условие
P2(x) для P1(x), такое чтобы P2(x) →P1(x)
было истинным, и так далее до тех пор, пока не получат такое достаточное условие
Pn(x) для Pn-1(x), что Pn(x)→Pn-1(x) и Pn(x) = S(x).
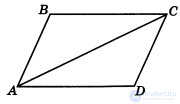
Пример: Доказать теорему «Если в четырехугольнике противоположные стороны попарно равны, то четырехугольник – параллелограмм» методом восходящего анализа.
Дано: АВСD – четырехугольник.
Доказать: ABCD – параллелограмм.
Доказательство
1. «Давайте вспомним определение, какой четырехугольник называется параллелограммом»
2. «По условию нам дано, что АВ=CD, АD=ВС»
3. «Значит для доказательства того, что четырехугольник ABCD является параллелограммом, достаточно доказать, что BC‖AD и AB‖СD.»
4. «Для доказательства параллельности сторон четырехугольника достаточно доказать равенство накрест лежащих углов, образуемых при пересечении двух прямых третьей.»
5. «Для этого проведем диагональ из ∟А в ∟С»
6. «У нас получились ∟АСВ и ∟САD; ∟ВАС и ∟ACD.»
7. «Для доказательства равенств ∟АСВ = ∟САD и ∟ВАС = ∟ACD достаточно доказать равенство треугольников АВС и CDA.»
8. «У нас получились два треугольника: ΔАВС и ΔАDС»
9. «Теперь мы докажем, что эти треугольники равны. Как это можно сделать?»
10. «АВ=CD, АD=ВС по условию, АС – общая сторона, значит треугольники равны по третьему признаку.»
11. «Если треугольники равны, то будут равными и углы внутри треугольников, значит ∟АСВ = ∟САD и ∟ВАС = ∟ACD»
12. «Так как ∟ВАС =∟ACD, то прямые АВ и СD параллельны: AB ∥ CD по признаку параллельности прямых.»
13. «Аналогично, так как ∟АСВ = ∟САD, то прямые ВС и АD параллельны: ВС ‖АD по признаку параллельности прямых»
14. «Теорема доказана»
Нисходящим анализом (несовершенным анализом) называют такую разновидность аналитического метода, при которой, отталкиваясь от заключения P(x) рассуждения ведут путем последовательного получения логических следствий:
P(x) ⇒ P1(x) ⇒ P2(x) ⇒ … ⇒Pn(x),
где Pn(x) есть предложение, истинное значение которого нам точно известно. При выведении следствий из P(x) временно допускают, что оно истинно. При нисходящем анализе, так же как и при восходящем, рассуждения ведут от заключения теоремы, но подбирают уже не достаточные условия, а необходимые.
Выведение необходимых условий продолжают до тех пор, пока не придут к очевидному следствию, представляющему собой или условие теоремы, или ранее изученное истинное утверждение. Если окажется возможным провести рассуждения в обратном порядке, при котором условие теоремы или очевидное утверждение выступают отправной посылкой, то получим искомое доказательство.
Пример: Выполнить нисходящий анализ для доказательства теоремы: «Если в четырехугольнике противоположные стороны попарно равны, то четырехугольник – параллелограмм.»
Дано: ABCD – четырехугольник,
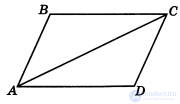
Доказать: ABCD – параллелограмм.
Доказательство:
1. «Предположим, что ABCD – параллелограмм.»
2. «Тогда BC = AD и AB = CD.»
3. «Проведем диагональ АС. Тогда ∟ACB = ∟CAD, ∟BAC = ∟ACD как накрест лежащие углы при параллельных прямых и секущей.»
4. «У нас получились два равных треугольника:»ΔABC = ΔCDA, они будут равны по стороне АС и двум прилежащим к ней углам).
5. «Раз треугольники равны, то будут равными и стороны: AB = CD, AD =BC, AC = AC»
6. «Мы доказали истинность предположения, которое поставили в начале нашего доказательства. Значит мы доказали, что данный четырехугольник является параллелограммом.»
Цель нисходящего анализа – поиск доказательства. Само доказательство проводится в обратном порядке и в итоге получится синтетическое доказательство.
Аналитико-синтетический метод доказательства заключается в том, что в процессе доказательства происходит последовательное преобразование то условия теоремы, то заключения.
Пример: доказательство теоремы: «Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник параллелограмм».
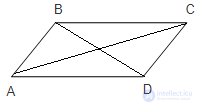
Дано: ABCD – четырехугольник,
AB = CD, AD =BC.
Доказать: ABCD – параллелограмм.
Доказательство:
Требуется доказать, что ВС‖ АД.
Для этого достаточно доказать, чтобы внутренние накрест лежащие углы ∟ВСО и ∟ОАD, образованные прямыми ВС и АD и секущей АС были равны.
А для того, чтобы доказать, что эти углы равны надо доказать равенство ∟ВОС и ∟DОА, и что интересующие нас углы лежат против соответственно равных сторон. В последнем убеждаешься из чертежа, так как ВО=ОD по условию.
Для того, чтобы ΔВОС и ΔDОА были равны достаточно доказать либо первый, либо второй, либо третий признак равенства треугольников. В данном случае нам удобнее доказать первый признак, т.к. ВО=ОD и СО=ОА по условию теоремы, а ∟ВОС = ∟DОА, как вертикальные.
Далее составляем схему проведенного анализа:
|
Чтобы доказать -> |
Надо доказать |
| I. ВС || АD | II. ∟ВСО=∟ОАD, как внутренние накрест лежащие, образованные прямыми ВС, АD и секущей АС |
| II. ∟ВСО=∟ОАD | III. ∟ВОС=∟ DОА, и углы ВСО и ОАD лежат против равных сторон |
| III. Δ ВОС= Δ DОА | IV. Равенство трех его элементов и определить признак равенства треугольников ОА=ОС – по условию ВО=ОD – по условию ∟АОД=∟СОВ – вертикальные Δ ВОС= ΔDОА по I. признаку |
| ТО | <- ЕСЛИ |
То II>III>IV), перебираясь, каждый раз от заключения к его основанию, происходит рассуждение по схеме: «чтобы доказать (I), надо доказать (II) и т.д.»
Проще говоря, мы создаем некую цепь определенных действий и условий: каждое верхнее суждение есть необходимое условие для нижнего. После проведенного анализа нужно воссоединить все в одно целое, т.е. провести синтез. Предположим, что будет проводиться рассуждение справа налево (IV>III>II>I), нанизывая цепь достаточных условий от основания к заключению, и рассуждая так: «если IV, то III, если III, то II и т.д.»
Метод от противного заключается в том, что доказательство теоремы начинают с предположения, что из S(x) не следует P(x). Тогда имеет место истинность утверждения S(x) и ложность утверждения P(x). Из утверждения S(x) выводят следствия до тех пор, пока не получат следствие, находящееся в противоречии либо с условием теоремы, либо с ранее изученным теоретическим фактом. Данный метод основан на использовании закона контрапозиции:
Нисходящий анализ является составной частью способа доказательства от противного.
Пусть S – совокупность доказанных теорем. Требуется доказать An ⇒Bn .
Допустим, что An ⇒Bn ложно, тогда истинно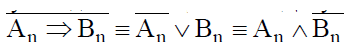 
(всякое высказывание либо истинное, либо ложное – закон исключения третьего).
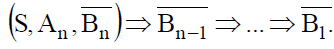
Пусть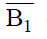 
отрицает истинность 
.
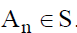В этом случае мы пришли к противоречию, абсурду, значит,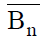 
ложно. Но тогда Bn отклоняется.
По закону исключенного третьего надо признать, что Bn истинно.
Доказательство приведением к нелепости является косвенным доказательством:
истинность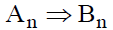 
устанавливается доказательством ложности .
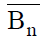Доказательству «от противного» присущи черты, общие с аналитическим методом. Оно начинается с рассмотрения того, что требуется доказать.
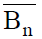разбивают на возможные случаи (элементарный анализ), и в любом случае показывается, что этот анализ приводит к противоречию.
Введя предложение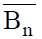 
, присоединяя его к совокупности известных предложений S получают следствия из 
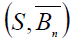, пока не достигают противоречивого следствия. Это сближает доказательство от противного с нисходящим анализом.
План доказательства «от противного» (А.В. Погорелов):
1. Допустим, что заключение теоремы ложно. Предположим, что верно предложение, противоположное тому, что утверждается в теореме.
2. Путем рассуждений, опираясь на аксиомы и теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом,
либо доказанной ранее теореме.
3. Наличие противоречий заставляет отказаться от принятого предложения.
4. Признаем правильность заключения доказываемой теоремы.
Содержание плана доказательства учащимся необходимо предложить передать своими словами.
Необходимо подготовить учащихся к тем ситуациям, которые встречаются при доказательстве теорем методом «от противного» (примеры
упражнений):
1) Даны два отрезка прямой а и b. Какие отношения могут быть между длинами этих отрезков?
2) с и d – два отрезка прямой: с ⩽ d . Какие отношения могут быть между длинами этих отрезков?
3) а и b– два отрезка прямой, причем a ≠ b. Какие отношения могут быть между длинами этих отрезков?
4) с и d – два отрезка прямой, причем с не меньше d. Какие отношения могут быть между длинами этих отрезков?
5) А и B – два угла. Угол А не меньше угла В. Какие заключения можно сделать о величинах этих углов?
6) С и D – два угла, причем ∟С ≠ ∟D, кроме того, угол С не больше угла D. Какое соотношение существует между углами С и D?
7) АВ и СD – две прямые, принадлежащие одной плоскости. Какие возможны случаи взаимного расположения этих прямых?
Пример: Докажем теорему «Разносторонний треугольник нельзя разбить на два равных треугольника» методом от противного.
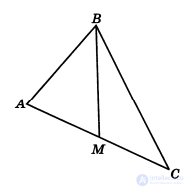
Доказательство:
1) Пусть ΔАВМ=ΔВМС, АВ ≠ВС ≠АС.
2) В этих равных треугольниках ВМ — общая сторона и по теореме о том, что в равных треугольниках против равных сторон лежат равные углы, заключаем, что ΔВАМ = ΔВСМ.
3) По теореме о том, что если углы при основании треугольника равны, то треугольник равнобедренный, заключаем, что АВ = ВС.
4) Мы получили, что АВ = ВС, но по условию теоремы АВ≠ВС. Получили противоречие.
5) Значит, наше предположение неверно, а верно то, что ΔАВМ ≠ ΔВМС.
1. На какие виды делятся доказательства?
2. что такое доказательсво?
3. что такое опровержение?
В общем, мой друг ты одолел чтение этой статьи об доказательство. Работы впереди у тебя будет много. Смело пиши комментарии, развивайся и счастье окажется в твоих руках. Надеюсь, что теперь ты понял что такое доказательство, опровержение, доказательство в широком смысле и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Логика
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Логика
Термины: Логика