Привет, Вы узнаете о том , что такое классификация суждений, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое классификация суждений, простые суждения, сложные суждения, проблематичные суждения, достоверные суждения , настоятельно рекомендую прочитать все из категории Логика.

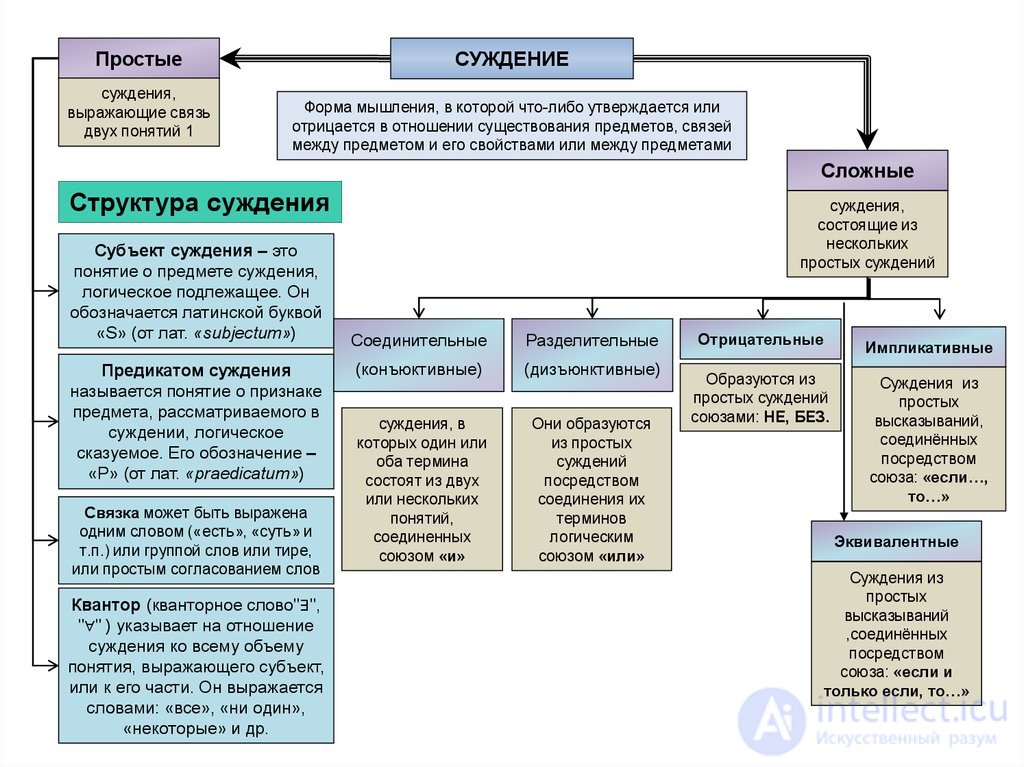
1) По степени сложности все суждения делят на две обширные группы (два типа) – простые и сложные.

простые суждения – это суждения, в которых нельзя выделить правильную часть, являющуюся самостоятельным суждением.

сложные суждения – это суждения, состоящие из двух или более простых суждений.

Поскольку суждение является смыслом высказывания, все сказанное о делении высказываний на группы относится и к классификации суждений. Их можно, прежде всего, разделить на простые исложные суждения. Первые не содержат других суждений в качестве своих частей, в сложных суждениях некоторые их части сами являются суждениями. Среди простых суждений особую роль играют так называемые категорические суждения, образуемые с помощью логических связок «Все... есть», «Все... нс есть», «Некоторые... есть...» и «Некоторые... не... есть».

Категорические суждения не исчерпывают всего класса простых суждений. Простыми являются также суждения об отношениях, подобные «А равно В», «А меньше В».

«А дальше В», «А раньше В» и т.д. Эти суждения не сводимы к суждениям со связкой «есть». Если пользоваться только языком, включающим лишь категорические суждения, не удастся выразить большую часть математики, физики и других наук.

2.1. Простые суждения

Простые суждения раскрывают безусловную связь между предметами мысли (поэтому их называют еще категорическими). С точки зрения функции они служат отражением одной-единственной связи объективного мира.

Простые суждения делятся на виды по следующим основаниям:

• по характеру связки;

• по характеру субъекта;

• по характеру предиката;

• по отношению между субъектом и предикатом.

Виды суждений по качеству и количеству

Качество суждения – характеристика суждения по его логической форме как утвердительного или отрицательного. Определяется характером связки («есть», или «не есть»).

Утвердительное суждение – суждение, раскрывающее наличие какой-либо связи между субъектом и предикатом.

Общая формула утвердительного суждения «S есть Р».

Отрицательное суждение – суждение, раскрывающее отсутствие той или иной связи между субъектом и предикатом.

Общая формула отрицательного суждения «S не есть Р».

В свою очередь отрицательное суждение может быть: а) с положительным предикатом («петров не есть патриот»), б) с отрицательным предикатом («Петров не есть непатриот»).

Количество суждения – характеристика суждения по логическому объему его субъекта как общего, частного или единичного.

Общее суждение – суждение, в котором что-либо утверждается обо всей группе предметов в разделительном смысле («все», «всякий», «каждый» – в утвердительных, и, соответственно», «ни один», «никто», «никакой» – в отрицательных суждениях).

В свою очередь общие суждения могут быть выделяющими и невыделяющими.

Выделяющее суждение нечто говорится лишь о данной группе («только», «лишь», например, «Только суд осуществляет правосудие»).

Невыделяющие суждения предполагают, что содержащееся в них утверждение может быть верно и для других групп (например, суждение «Все адвокаты – юристы» не отвергает того, что помимо адвокатов юристами являются прокуроры, следователи и пр.).

Частные суждения – суждения, в которых что-либо высказывается о части какой-то группы предметов («некоторые», «не все», «большинство», «часть», «отдельные» и др.). Это суждения по формуле «Некоторые S есть (не есть) Р».

Частные суждения делятся на определенные и неопределенные.

Определенные частные суждения – суждения в которых, утверждаемое относительно части какой-то группы предметов не может быть распространено на всю группу предметов в целом. Слова «некоторые» здесь подразумевают «только некоторые» (например, «некоторые люди красивы», некоторые книги не интересны»).

Неопределенные частные суждения – суждения, в которых высказанное относительно части предметов группы, может быть отнесено и ко всей группе вообще. Слово «некоторые» здесь подразумевает «по крайней мере некоторые, а может быть и все».

Единичные суждения – суждения, в которых нечто высказывается об отдельном предмете мысли («это»). Формула «Это S есть (не есть) Р» (Солнце – источник жизни на Земле», «Луна – не планета»).

В качестве единичных выступают суждения об индивидуальном предмете, и суждения о совокупности предметов, рассматриваемых как единое целое и выражаемых собирательными понятиями.

Промежуточное положение между общими и частными суждениями занимают исключающие суждения­, когда в одном высказывании встречаются и квантор «все», и ограничение «кроме» (или «за исключением», «как правило» и пр.). Например: «Все студенты, за исключением двоих, пришли на лекцию».

Объединенная классификация суждений по их количеству и качеству:

Общеутвердительные – суждения, по количеству (по характеру субъекта) – общие, а по качеству (по характеру связки) – утвердительные.

(например, «Все адвокаты – юристы»)

Частноутвердительные – суждения, по количеству (по характеру субъекта) – частные, а по качеству (по характеру связки) – утвердительные.

(например, «Некоторые свидетели дают достоверные показания»)

Общеотрицательные – суждения, по количеству (по характеру субъекта) – общие, а по качеству (по характеру связки) – отрицательные.

(например, «Ни один обвиняемый не оправдан»)

Частноотрицательные – суждения, по количеству (по характеру субъекта) – частные, а по качеству (по характеру связки) – отрицательные.

(например, «Некоторые свидетели не дают верных показаний»)

Для формульной записи этих видов суждений в логике используются гласные буквы латинских слов «affirmo» («утверждаю») и «nego» («отрицаю»):

A – общеутвердительные;

I – частноутвердительные;

E – общеотрицательные;

O – частноотрицательные.

Для правильного оперирования суждениями необходимо знать распределенность терминов в них – субъекта и предиката.

Распределенным считается термин, мыслимый во всем объеме; нераспределенным – если он мыслится не во всем объеме.

В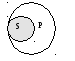общеутвердительных суждениях (А): «Все S есть Р» – субъект распределен, а предикат не распределен (заливкой на схеме отмечена степень их распределенности).

Исключение составляют лишь случаи, когда суждение общевыделяющее. Например, «Только люди – разумные существа на Земле». В них распределен не только субъект, но и предикат.

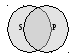
В частноутвердительных суждениях (I): «Некоторые S есть Р» – субъект и предикат не распределены.

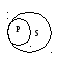
Исключение составляют лишь случаи, когда субъект по объему шире предиката. Например: «Некоторые смертные существа – люди», «Некоторые юристы – адвокаты». В них субъект не распределен, а предикат распределен.

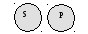В общеотрицательных суждениях (Е): «Ни одно S не есть Р» – субъект и предикат распределены.

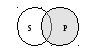
+В частноотрицательных суждениях (О): «Некоторые S не есть Р» – субъект не распределен, предикат распределен.

Таким образом, наблюдается следующая закономерность:

а) субъект распределен в общих и не распределен в частных суждениях;

б) предикат распределен в отрицательных и не распределен в утвердительных суждениях.

Виды суждений по характеру предиката

Атрибутивные суждения (от лат. attributum – свойство, признак), или суждения о свойствах чего-либо, раскрывают наличие или отсутствие у предмета мысли тех или иных свойств (или признаков).

(например, «Все республики бывшего СССР объявили о своей независимости»)

В содержательном плане это суждение о том, обладает или не обладает предмет мысли какой-либо совокупностью свойств (тогда предикат выражен конкретным понятием, например, «Медь – металл») или отдельным свойством (тогда предикат выражен абстрактным понятием, например, «Медь – электропроводна»).

В объемном плане атрибутивные суждения – это суждения о том, входит или не входит предмет мысли в тот или иной класс предметов – «суждения включения (или невключения) в класс предметов». В символической логике выражается формулами: S Р (читается: объем S входит в объем Р) и S Р (читается: S принадлежит Р).

Реляционные суждения (от лат. Об этом говорит сайт https://intellect.icu . relatio – отношение), или суждения об отношениях чего-либо к чему-либо, раскрывают наличие или отсутствие у предмета мысли того или иного отношения к другому предмету (или нескольким предметам).

Обычно выражаются формулой x R y, где x и y – предметы мысли, а R (от relatio) – отношение между ними.

(например: «Росссия не равно СССР», «Москва больше Санкт-Петербурга»)

Разновидности реляционных суждений:

суждения об отношениях между двумя предметами;

суждения об отношениях между тремя и более предметами (предикат в данном случае – «многоместный» («Рязань находится между Москвой и Тамбовом»).

В современной логике есть тенденция свести реляционные суждения к атрибутивным. Например, суждение «Рязань меньше Москвы» (реляционное) можно представить как суждение «Рязань принадлежит к городам, которые меньше Москвы» (атрибутивное).

Экзистенциальные суждения (от лат. exsistentia – существование), или суждения о существовании чего-либо, это такие, в которых раскрывается наличие или отсутствие самого предмета мысли.

Предикат выражается словами «существует» («не существует»), «есть» («нет»), «был» («не был»), «будет» («не будет») и др.

Виды суждений по характеру предиката имеют важное познавательное значение. В атрибутивные суждения облекаются знания о все новых открываемых свойствах разнообразных предметов мысли. В реляционных суждениях отражается бесконечное богатство отношений между предметами мысли: пространственные и временные, природные и социальные (политические нравственные, религиозные, семейные, правовые и пр.). Экзистенциальные суждения позволяют формулировать наши мысли о важнейших проблемах существования (или отсутствия) тех или иных предметов и явлений: есть ли жизнь на других планетах, существует ли «биополе», «телепатия», «полтергейст», или, например, имело ли место событие преступления.

Виды суждений по модальности

Модальность суждения (от лат. modus – образ, способ) – характеристика суждения в зависимости от его степени возможности, необходимости, обязательности и т.п.

Это информация об объективном характере (или способе) связи между субъектом и предикатом, раскрываемой в суждении, о субъективном отношении к ней человека, характере и степени достоверности заключенного в суждении знания и т.д. В языке модальность суждения выражается посредством множества слов. Например, таких, как «возможно», «разрешено», «ценно», а также их отрицаний («невозможно», «не разрешено» и пр.

Алетическая, или истинная модальность (от греч. aleteja – истина) – выражает характер связи между мыслимыми предметами, а следовательно, между субъектом и предикатом суждения. Модальный оператор «необходимо» или «возможно».

С точки зрения алетической модальности различают следующие разновидности суждений:

а) ассерторические суждения, или суждения о факте, действительности чего-либо. В таких суждениях модальность не выражена, а констатируется лишь самый факт чего-либо (например: «Россия переходит к рыночной экономике»);

б) проблематические суждения, или суждения о возможности чего-либо (например: «Россия может перейти к рыночной экономике»);

в) аподиктические суждения, или суждения о необходимости чего-либо (например: «Россия по необходимости перейдет к рыночной экономике»).

Деонтическая, или нормативная, модальность (от греч. deon – нужное, должное) – характеристика суждений о деятельности людей с позиции отношений должествования (через операторы «обязательно», «разрешено», «запрещено» и им подобные).

Основные разновидности деонтической модальности:

а) суждения о наличии или отсутствии какого-либо права. Формулируются с помощью слов «разрешено», «запрещено», «вправе» и др. (например: «Каждый имеет право на жизнь», или «Принудительный труд запрещен»);

б) суждения о наличии (или отсутствии) какой-либо обязанности. Формулируются с помощью слов «обязан», «должен», «необходимо» и др.

Эпистемическая, или познавательная модальность (от греч. episteme – знание) – характеристика суждений с позиции степени достоверности знания. Логические операторы «доказуемо», «недоказуемо», «опровержимо» и пр.

Основные разновидности эпистемической модальности:

а) суждения, основанные на вере, независимо от того, религиозная она или нет. Например: «Верю, что Бог существует», «Верю в наступление лучшей жизни»;

б) суждения, основанные на знании, независимо от того, проблематичные они или нет (достоверные). Например: «Во Вселенной, по-видимому, есть другие разумные существа», «Телепатия, вероятно, существует», «На Марсе достоверно отсутствие жизни».

Аксиологическая, или ценностная, модальность (от греч. axios – ценный) – выражает ценностное отношение человека к предмету мысли. Операторы «хорошо», «плохо», «безразлично» и пр. Например: «Плохо жить без друзей», «Хорошо иметь домик в деревне».

2.2. Сложные суждения

Сложные суждения образуются из простых суждений с помощью логических связок: конъюнкции, дизъюнкции, импликации, эквивалентности и отрицания.

Истинность или ложность сложных суждений зависит, прежде всего, от истинности или ложности составляющих его простых или иных суждений.

В языке сложные суждения выражаются сложносочиненными, сложноподчиненными, а иногда и простыми распространенными предложениями (в последнем случае мы имеем дело с своеобразным свертыванием сложных предложений, например, вместо сложносочиненного предложения «Аристотель был великим логиком, и Гегель тоже был великим логиком» можно сказать: «Аристотель и Гегель были великими логиками»).

Виды сложных суждений по характеру логического союза

1. Конъюнктивные (или соединительные) суждения (от лат. conjunctio – связь, соединение). Образуются из исходных посредством логического союза конъюнкции «и» (символически «»). Наиболее общая схема: АВ (читается: «А и В»), где А и В – исходные суждения, а знак– символ их конъюнкции. Например: «Никто не забыт, и ничто не забыто».

Помимо союза «и» в языке конъюнкция может отображаться другими грамматическими союзами («а», «но», «да», «хотя», «а также»).

Если конъюнкция выражена простым распространенным предложением, то она может иметь три исходные структуры:

а) один субъект и два предиката – «S есть (не есть) Р₁ и Р₂». Например: «Все равны перед законом и судом» (исходные суждения: «Все равны перед законом» и «Все равны перед судом»);

б) два субъекта и один предикат – «S₁ и S₂ есть (не есть) Р». Например: «Государственные пенсии и социальные пособия устанавливаются законом» (здесь также два исходных суждения);

в) два субъекта и два предиката – «S₁ и S₂ есть (не есть) Р₁ и Р₂». Например: «Основные права и свободы человека неотчуждаемы и принадлежат каждому от рождения» (здесь уже четыре простых суждения).

Могут быть и боле сложные конструкции.

Возможны четыре способа сочетания двух исходных суждений «А» и «В» в зависимости от их истинности («и») и ложности («л»). Конъюнкция таких суждений истинна, если истинно каждое из них в отдельности.

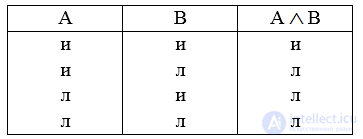
Логический союз «и» может соединять и более двух исходных суждений – по формуле: АВС. В подобных случаях важно, чтобы исходные суждения обладали свойством ассоциативности (сочетаемости), т.е. их истинность или ложность не менялись от способа сочетания: (АВ)С или А(ВС) и т.д.

2. Дизъюнктивные (разделительные) суждения (от лат. disunctio – разобщение, обособление).

Слабая (нестрогая) дизъюнкция образуется логическим союзом «или» (знак ). Характеризуется тем, что объединяемые суждения не исключают друг друга. Общая формула: АВ (читается «А или В»). Языковые средства выражения слабой дизъюнкции – грамматические союзы «или», «либо» и другие в их разделительно-соединительном значении. Например: «Право может способствовать экономическому развитию либо препятствовать ему».

Слабая дизъюнкция истинна в тех случаях, когда истинно по крайней мере одно из составляющих ее суждений (или оба вместе), и ложна, когда оба суждения ложны:

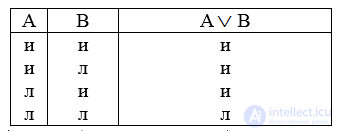
Сильная (строгая) дизъюнкция образуется логическим союзом «либо… либо» (символ 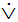). Ее составляющие исключают друг друга. Общая формула «А 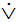В» (читается «А либо В»). Выражается теми же грамматическими средствами, что и слабая («или», «либо»), но уже в разделительно-исключающем значении. Например: «Закон, устанавливающий или отягчающий ответственность, обратной силы не имеет».

Строгая дизъюнкция истинна лишь тогда, когда одно из составляющих ее суждений истинно, а другое ложно:

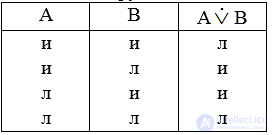
Дизъюнктивное суждение может включать в себя три и более исходных суждения. Формула А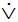 В С…

3. Импликативные (или условные) суждения (от лат. implicatio – сцепление, тесная связь).

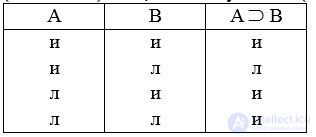
В них объединяются суждения на основе логического союза «если… то» (обозначается → ). Формула А→В (читается: «Если А, то В»). В условных суждениях отражаются зависимости между предметами и явлениями – причинно-следственные, пространственно-временные, функциональные и т.д. В классической логике импликация обозначается знаком (АВ) и называется материальной импликацией.

Импликация истинна во всех случаях, кроме одного: когда предшествующее (основание) есть, а последующего (следствия) нет.

4. Эквивалентные (равнозначные) суждения (от лат. aequivalens – равноценный, равнозначный).

В них объединяются суждения с взаимной (прямой и обратной) условной зависимостью. Они называются еще двойной импликацией. Их образует логический союз «если и только если… то» (символ 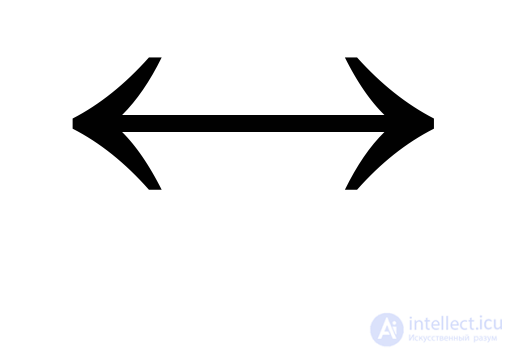). Формула эквивалентности А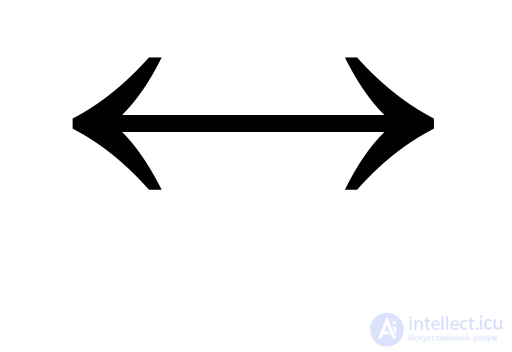В (читается: «если и только если А, то В»). Пример: «Если и только если человек достиг пенсионного возраста, то он имеет право на получение пенсии по возрасту».

Для обозначения обобщенной эквивалентности, независимой от конкретного содержания образующих ее суждений, используется также знак «».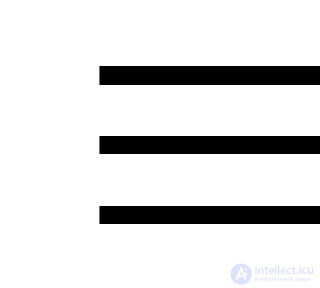

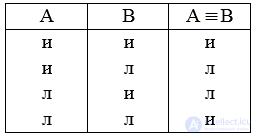
Эквивалентное суждение истинно в двух случаях: когда оба составляющих его суждения истинны и когда они оба ложны.

5. Отрицание суждений.

Логический союз «неверно, что» или просто «не» (знак отрицания или 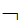). В отличие от бинарных союзов он относится к одному суждению. Прибавление его к какому-либо суждению означает образование нового суждения. Например, исходное суждение: «Все судьи неподкупны». Его отрицание: «Неверно, что все судьи неподкупны» или «Не все судьи неподкупны».

Отрицание истинно, если исходное суждение ложно, и наоборот:

По степени обоснованности

Фактор логического воздействия — это принятие суждения как истинного или ложного в силу его обоснованности другими суждениями, из которых принимаемое суждение логически вытекает как следствие. Особенность рационально ориентированного познания — принятие лишь таких суждений, которые опираются на достоверно установленный эмпирический или теоретический фундамент из проверенных суждений. Такого рода обоснованные суждения приобретают эпистемический статус знаний: К(р), где К — модальный оператор, обозначающий «знание».

По степени обоснованности среди знаний различают два непересекающихся класса суждений:

1) достоверные и

2) проблематичные.

1) достоверные суждения — это достаточно обоснованные истинные или ложные суждения. Их истинность или ложность устанавливается либо путем непосредственной проверки, либо опосредованно, когда суждение подтверждается эмпирическими или теоретическими положениями.

Модальность таких суждений можно выразить с помощью операторов: доказанности (верифицированности) — V и опровергнутости (фальсифицированности) — F. Суждение р доказано, если оно достаточно обосновано: Vp. Если достаточно обосновано отрицание суждения, т. е. не-p, то такое суждение также считается доказанным: V˥р. Например, доказано суждение «Неверно, что Н. принимал непосредственное участие в совершении преступления», если установлено алиби, т. е. факт пребывания Н. во время совершения преступления в другом месте.

Таким образом, о любом достоверно установленном суждении можно говорить как о доказанном, или верифицированном, т. е. .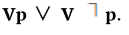

Достоверные суждения могут быть выражены с помощью оператора опровергнутости: Fр ∨ F˥р.

Операторы доказанности и опровергнутости могут быть выражены один через другой. Так, доказанность р эквивалентна опровержению не-p, а доказанность не-p эквивалентна опровержению р. Эту эквивалентность можно представить в следующем виде:

Vp ≡ F˥р;

V˥р ≡ Fр.

Достоверность относится к такой модальной характеристике суждения, которая, подобно понятиям истины и ложности, не изменяется по степеням. О двух высказываниях нельзя сказать, что одно из них «более достоверно», чем другое. В случае достаточной обоснованности суждения его считают доказанным, тем самым достоверным, т. е. истинным или ложным без изменения по степеням.

Следует отметить, что в психологическом плане достоверное знание характеризуется отсутствием сомнений в истинности соответствующего суждения. Однако отсутствие сомнений само по себе еще не говорит о достоверности суждения, которое признается таковым лишь при наличии соответствующих оснований — логических или эмпирических.

2) проблематичные суждения — это суждения, недостаточно обоснованные. Истинность или ложность таких суждений точно не установлена, поэтому их называют проблематичными, правдоподобными, или вероятными.

В естественном языке показателями проблематичности суждения обычно служат вводные слова: «по-видимому», «вероятно», «представляется», «возможно», «можно предположить» и др. Для проблематичных суждений принято выражение: «S, вероятно, есть Р». Проблематичность какого-либо суждения (р) можно выразить оператором Р; выражение Рр читается: «Вероятно, р».

Проблематичность суждения р может быть выражена в терминах доказанности и опровергнутости:

В судебном исследовании в форме проблематичных суждений строятся версии (гипотезы) об обстоятельствах расследуемых дел. Они направляют расследование по правильному руслу и помогают установлению достоверных результатов.

Требование доказанности предъявляется ко всем суждениям в судопроизводстве. Судебный обвинительный приговор по уголовному делу и решение суда по гражданскому делу должны опираться на достоверно установленные обстоятельства каждого конкретного дела. Только в этом случае решение суда считается правосудным.

Обоснованность проблематичных суждений может быть представлена в терминах теории вероятности. Логическая вероятность суждения означает степень его обоснованности. Если обозначить вероятность символом Р, то для любого суждения р его вероятность принимает значение 0 ≤ Р(р) ≤ 1. 0 и 1 выступают пределами обоснования, выражая достоверное значение. Так, Р(р) = 0 означает, что р фальсифицировано, или опровергнуто (р ложно). Поскольку вероятность проблематичного суждения принимает числовое значение в интервале между 0 и 1, т. е. 0 < Р(р) < 1, ее обычно выражают дробью, например, Р(р) = 1/3 или Р(р) = 0,2. Если Р(р) = 1, это означает, что р верифицировано, или доказано (р истинно).

В простейших случаях, когда оперируют однотипными и равными по их логической силе основаниями, степень вероятности суждения определяется отношением числа благоприятных оснований (m) к общему их числу (n): Р(р) = m/n. Так, если для суждения р из 10 оснований (n) 8 оказались благоприятными (m), то степень его обоснованности, или логической вероятности, будет выражаться дробью 8/10 = 4/5, т. е. Р(р) = 4/5.

В случае благоприятности всех 10 возможных оснований вероятность будет выражаться соотношением Р(р) = 10/10 = 1. Это значит, что высказывание р считают достоверным. Если все 10 оснований окажутся неблагоприятными, то вероятность р будет равна 0: Р(р) = 0/10 = 0. Это означает, что р оценивается как ложное.

В большинстве случаев в качестве оснований выступают разнотипные и различные по доказательной силе высказывания. Их обычно оценивают содержательно, с учетом различного «веса» каждого из них. В обычных рассуждениях нередко прибегают к следующей приблизительной градации вероятностей:

1) Р(р) = 1/3 — «р» маловероятно;

2) Р(р) = 1/2 — «р» равновероятно;

3) Р(р) > 1/2 — «р» более вероятно, чем нет;

4) Р(р) > 2/3 — «р» весьма вероятно.

Практически и теоретически обоснованные оценочные стандарты дают возможность объективно определять в вероятностной форме действительное логическое значение проблематичных суждений.

Обоснованность как объективную логическую характеристику суждения следует отличать от понятия уверенности, выражающего субъективно-психологическое отношение человека к высказыванию, его готовность принять или отвергнуть соответствующее суждение. Когда говорят, например, «Я уверен, что X совершил преступление»; «Я убежден, что свидетель заблуждается»; «Я считаю, что обвиняемый неверно описывает обстоятельства преступления», то, как правило, выражают субъективное отношение к содержанию высказываний — склонность принять или отвергнуть выраженную в них информацию.

Когда исследователь проявляет беспристрастность и ставит своей задачей найти объективную истину, его чувство уверенности определяется рациональными, логическими основаниями и зависит прежде всего от степени обоснованности суждения.

Если вероятностная оценка суждения прямо влияет на степень уверенности, то обратное имеет место не всегда. Высокая степень уверенности не означает, что она возникла как результат обоснованности суждения. Помимо логических оснований, чувство уверенности может возникнуть под влиянием и других, внелогических факторов, которые не всегда явно осознаются и не всегда контролируются. К ним относятся различного рода интересы, утилитарные соображения, субъективные склонности, привычки и т. п. Желаемое в этом случае непреднамеренно может быть выдано за действительное.

Именно поэтому при анализе важного в практическом отношении суждения следует различать такие логически проверяемые модальные характеристики, как степень обоснованности и субъективное чувство уверенности в истинности этого суждения. В научном исследовании, в деятельности юриста обоснованность суждения, выражаемая в соответствующей мотивировке, должна быть ведущим фактором, определяющим формирование субъективной уверенности, без которой также не бывает раскрытия истины.

Вопросы для самопроверки

• проблематичное суждение требующие дальнейшей проверки и подтверждение называется

Вау!! 😲 Ты еще не читал? Это зря!

• логический квадрат , сравнимые суждения ,
• простые суждения ,
• сложное суждение , правила истинности ,
• суждение , абстрактная мысль ,
• суждения , суждение ,
• занимательные задачи , задачи по логике ,
• тесты по логике ,
• тесты по логике ,
• тесты по логике ,
• тесты по логике ,
• тесты по логике ,
• законы логики , закон тождества ,
• термины по логике , понятия логики ,
• суждение , абстрактная мысль ,
• умозаключение , абстрактная мысль ,
• понятие , абстрактная мысль ,

В общем, мой друг ты одолел чтение этой статьи об классификация суждений. Работы впереди у тебя будет много. Смело пиши комментарии, развивайся и счастье окажется в твоих руках. Надеюсь, что теперь ты понял что такое классификация суждений, простые суждения, сложные суждения, проблематичные суждения, достоверные суждения и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Логика

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.