Лекция
Сразу хочу сказать, что здесь никакой воды про язык логики предикатов, и только нужная информация. Для того чтобы лучше понимать что такое язык логики предикатов, логика предикатов, предикат , настоятельно рекомендую прочитать все из категории Логика.
В современной логике разработано несколько специальных искусственных языков, применяемых для описания ее законов. Наиболее широко для этой цели используется язык логики предикат ов , поражения которого точно определяются, что позволяет избегать двусмысленностей и сводить процесс проверки правильности рассуждений к «вычислениям», а также решать ряд других проблем.
Как и в естественных языках, в этом языке есть алфавит и сложные выражения.
Язык логики предикатов - это один из искусственных языков современной формальной логики. Прежде чем мы приступим к его рассмотрению, уточним, какие языки называют естественными и искусственными и как они соотносятся друг с другом.
Естественные языки - это языки естественных коллективов: русский, немецкий, китайский и т.д. Все остальные языки имеют искусственный характер.
Естественный и искусственный языки противоположны друг другу. Чтобы убедиться в этом, отметим основные различия между ними.
Во-первых, они различаются по характеру возникновения. Естественный язык возникает стихийно, его никто специально не создает. Людям нужно общаться друг с другом, а без языка это невозможно. Вот и возникает язык, причем возникает естественно, без предварительного обдумывания. Напротив, искусственный язык сначала кто-то придумывает, и лишь потом он приступает к выполнению своей роли посредника в общении.
Из особенностей возникновения вытекает второе различие: у естественного языка нет конкретных авторов, а у искусственного хотя бы один такой автор обязательно есть. Возьмем для примера русский язык. Можно ли говорить, что его кто создал? Можно: его создал народ. Но при этом ни один представитель русского народа не может претендовать на авторство по отношению к своему языку. Этот язык создавали не какие-то конкретные авторы, а весь народ. Другое дело - искусственные языки. Мы можем не знать их конкретных авторов, как это, к примеру, имеет место в случае с древними шифрами, но то, что у каждого искусственного языка есть хотя бы один такой создатель, не вызывает сомнений. Иногда об авторе говорит имя искусственного языка. Яркий пример - язык, широко известный под названием "азбука Морзе".
В-третьих, естественный и искусственный языки различают по сфере применения: у первого она универсальная, а у второго - локальная. Универсальность применения естественного языка означает то, что он используется во всех без исключения видах деятельности. А вот искусственный язык применяется не везде. Это и означает локальный характер применения. Вернемся к языку Морзе. Где его используют? Как правило, там, где нужно передавать информацию с помощью электромагнитных волн.
В-четвертых, естественный и искусственный языки - это качественно разные системы. Первый из них - открытая система, т.е. система незавершенная и принципиально не завершаемая. Поскольку деятельность людей развивается, должен развиваться и их родной язык. Об открытом характере любого естественного языка как системы говорит наличие в нем таких выражений, которые являются исключениями из правил, но используются при этом наравне с правильными выражениями.
Другое дело - искусственный язык. В идеале это - закрытая (законченная, завершенная) система, в которой все идет строго по правилам, в которой нет каких-либо исключений из правил. Наличие хотя бы одного неправильного выражения считается крупным недостатком искусственного языка, и этот недостаток стараются как можно быстрее устранить.
Основные различия естественного и искусственного языков можно представить в виде таблицы:
| Основание сравнения | Естественный язык | Искусственный язык |
| 1. Возникновение | Стихийное | Специально организованное |
| 2. Наличие конкретного автора | Нет | Есть |
| 3. Сфера применения | Универсальная | Локальная |
| 4. Специфика системы | Открытость | Закрытость |
Итак, естественный и искусственный языки настолько различаются по отношению друг к другу, что их следует рассматривать как противоположные знаковые системы. Однако, несмотря на противоположность, они сближаются, что особенно отчетливо видно в наше время.
С одной стороны, усилиями лингвистов создаются школьные учебники естественных языков. Изучение родного языка в школе обязательно для современного человека. Это делает естественное языковое общение более строгим, а строгость - одно из главных свойств искусственных языков. Сравните Россию начала ХХ и XXI веков. В начале ХХ века подавляющее большинство населения нашей страны говорило на диалектах русского языка, что не удивительно в условиях массовой безграмотности. Многочисленные диалекты затрудняли общение представителей разных регионов. В наше время ситуация совсем другая: большинство россиян говорит на одном и том же языке.
С другой стороны, искусственные языки становятся все более гибкими, и за счет этого вторгаются во все виды деятельности, т.е. приобретают универсальный характер применения, свойственный естественным языкам. Это легко проиллюстрировать на примере компьютерных языков. Сейчас без компьютеров не обходится ни одна из основных сфер современного общества, а работа на компьютере требует знать если не языки программирования, то хотя бы языки конкретных программ.
Сближение естественных и искусственных языков неминуемо приведет к их слиянию, но это произойдет не скоро. Искусственно ускорять сближение не следует, о чем говорит, в частности, история языка эсперанто. Он появился еще в конце XIX века как средство общения индоевропейских народов. При этом создатель эсперанто преследовал благую цель: чтобы никому не было обидно, пусть разные народы говорят на общем для них искусственном языке. По большому счету, затея провалилась. Да, эсперанто совсем не исчез: в современном международном общении его кое-где используют, но широкого распространения он не получил.
Теперь вернемся к логике. В настоящее время существует множество искусственных формально-логических языков. Их сотни, но все они строятся по сходным принципам, поэтому знакомство с одним из них позволяет при необходимости легко освоить другие.
Рассмотрим язык логики предикатов. В его алфавите следующие символы:
1) p, q, r, s, p1, … - пропозициональные переменные (символы для предложений); пропозициональные переменные (символы для (повествовательных) предложений, выражающих суждения), при исследовании рассуждений этими символами заменяются целые предложения;
2) a, b, c, d, a1, … - индивидные константы (символы для единичных имен); этими символами заменяются единичные имена;
3) x, y, z, x1, … - индивидные переменные (символы для общих имен);
4) P, Q, R, S, P1, … - предикаторы (символы для признаков, а также свойств и отношений);
5)  - логические термины, соответственно читаются «неверно, что» («не»), «и», «или», «если..., то...», «если и только если, то...» и называются знаком отрицания, конъюнкции, дизъюнкции, (материальной) импликации и (материальной) эквивалентности;
- логические термины, соответственно читаются «неверно, что» («не»), «и», «или», «если..., то...», «если и только если, то...» и называются знаком отрицания, конъюнкции, дизъюнкции, (материальной) импликации и (материальной) эквивалентности;
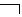 (знак отрицания, читается: "не" или "неверно, что"),
(знак отрицания, читается: "не" или "неверно, что"),
 (знак конъюнкции, т.е. соединения, читается: "и"),
(знак конъюнкции, т.е. соединения, читается: "и"),
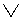 (знак нестрогой, или простой, дизъюнкции, т.е. нестрогого, или простого, разделения, читается: "или"),
(знак нестрогой, или простой, дизъюнкции, т.е. нестрогого, или простого, разделения, читается: "или"),
 (знак строгой дизъюнкции, читается: "или …, или"),
(знак строгой дизъюнкции, читается: "или …, или"),
 (знак импликации, читается: "если …, то"),
(знак импликации, читается: "если …, то"),
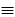 (знак эквивалентности, читается: "если и только если …, то"),
(знак эквивалентности, читается: "если и только если …, то"),
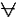 (квантор всеобщности, читается: "все", "всякий", "любой"),
(квантор всеобщности, читается: "все", "всякий", "любой"),
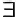 (квантор существования, читается: "существует такой …, что" или "некоторые") - логические символы;
(квантор существования, читается: "существует такой …, что" или "некоторые") - логические символы;
г)  , ... - k-местные предметные функторы, знаки k-местных предметных функций (k = 1, 2, 3, ...);
, ... - k-местные предметные функторы, знаки k-местных предметных функций (k = 1, 2, 3, ...);
д)  , ... Об этом говорит сайт https://intellect.icu . - k-местные предикаторные символы, или k-местные предикаторы (k = 1, 2, 3, ...); этими символами вменяются общие имена и знаки свойств и отношений, интерпретируемые в качестве общих имен
, ... Об этом говорит сайт https://intellect.icu . - k-местные предикаторные символы, или k-местные предикаторы (k = 1, 2, 3, ...); этими символами вменяются общие имена и знаки свойств и отношений, интерпретируемые в качестве общих имен ;
;
6) (, ) (скобки), , (запятая) - служебные символы.
Выражения языка логики предикатов называются формулами. Среди формул выделяют правильно построенные (ППФ).
Определению правильно построенной формулы предшествует определение терма:
а) индивидные константы и индивидные переменные являются термами;
б) если 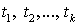 - термы, a
- термы, a 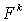 - k-местный предметный функтор, то выражение
- k-местный предметный функтор, то выражение  является термом;
является термом;
в) ничто иное не является термом.
Определение ППФ:
а) если  - термы, а
- термы, а  - k-местный предикатор, то
- k-местный предикатор, то 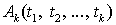 - ППФ1 (Если «
- ППФ1 (Если «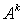 » - предикатор (общее имя или знак свойства или отношения, интерпретируемого в качестве общего имени, то выражение «
» - предикатор (общее имя или знак свойства или отношения, интерпретируемого в качестве общего имени, то выражение «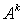 (...)» - сказуемое (предикат). Связка «суть» передается формой записи.); пропозициональная переменная есть ППФ;
(...)» - сказуемое (предикат). Связка «суть» передается формой записи.); пропозициональная переменная есть ППФ;
б) если A и В - ППФ, а  - индивидная переменная, то
- индивидная переменная, то  - ППФ;
- ППФ;
в) ничто иное не является ППФ
Таким образом, в алфавите представлены символы для основных семантических категорий. Строгий смысл знака отрицания и знаков логических связок (конъюнкции, дизъюнкции, импликации и эквивалентности) задают с помощью таблиц истинности. Если А и В - высказывания, 0 - ложь, а 1 - истина, в двузначной логике, т.е. в такой логике, где высказывание может быть либо ложным, либо истинным, а третьего не дано, эти таблицы имеют следующий вид:
|
|
Отметим, что представленные в таблицах логические символы различают по силе связывания, в порядке убывания которой они выстраиваются так: 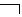 ,
,  ,
, 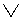 ,
,  ,
, 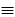 . Учет силы связывания позволяет сократить количество скобок в логических формулах. Пусть нам нужно исследовать на истинность формулу (p
. Учет силы связывания позволяет сократить количество скобок в логических формулах. Пусть нам нужно исследовать на истинность формулу (p 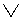 q)
q)  r ("если р или q, то r"). Так как дизъюнкция сильнее импликации, мы можем убрать скобки: p
r ("если р или q, то r"). Так как дизъюнкция сильнее импликации, мы можем убрать скобки: p 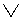 q
q  r. Читается полученная формула так же, как исходная. Иногда скобки убирать не следует. Например, в формуле (p
r. Читается полученная формула так же, как исходная. Иногда скобки убирать не следует. Например, в формуле (p  q)
q) 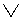 r ("если р, то q, или r") р и q связаны сильнее, чем q и r, а если убрать скобки, соотношение станет обратным.
r ("если р, то q, или r") р и q связаны сильнее, чем q и r, а если убрать скобки, соотношение станет обратным.
Логические формулы - это предложения искусственного языка символической (математической), т.е. современной формальной, логики. В них могут входить только символы алфавита, а записывать эти формулы, так же как и формулы математики, следует по правилам синтаксиса.
Определение правильно построенной формулы (ППФ) языка логики предикатов дается в четыре шага:
1) пропозициональная переменная является ППФ;
2) выражение вида A(t1, t2, …, tn), где A - предикатор, а tk - произвольный индивидный символ из данной в скобках последовательности, является ППФ;
3) если В и С - ППФ, а 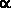 - индивидная переменная, то выражения вида
- индивидная переменная, то выражения вида 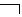 В, В
В, В С, В
С, В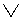 С, В
С, В С, В
С, В С, В
С, В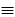 С,
С, 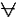
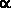 В,
В, 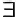
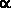 В - ППФ;
В - ППФ;
4) ничто иное не является ППФ.
Видно, что определение дано очень строго, и это не случайно: выше мы отмечали, что строгость - отличительное свойство искусственных языков.
Теперь приведем примеры формул языка логики предикатов. Возьмем пословицу "Язык до Киева доведет". Легче всего написать формулу для этого высказывания, используя пропозициональную переменную. Получится очень просто: р. Но по второму пункту определения ППФ мы можем построить более длинное предложение на языке логики предикатов: 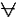 xP(x), где х - язык, Р - быть способным довести до Киева. Читается это предложение так: "Для любого х Р от х". Если мы учтем, что признак "быть способным довести до Киева" содержит двухместное отношение, то формула выйдет еще длиннее:
xP(x), где х - язык, Р - быть способным довести до Киева. Читается это предложение так: "Для любого х Р от х". Если мы учтем, что признак "быть способным довести до Киева" содержит двухместное отношение, то формула выйдет еще длиннее: 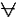 xP(x, a), где х - язык, а - Киев, Р - быть способным довести до (чего-либо).
xP(x, a), где х - язык, а - Киев, Р - быть способным довести до (чего-либо).
Что выражает любая логическая формула? Она выражает логическую форму данного высказывания, т.е. форму абстрактной мысли, которая в нем заключена. Эта форма предстает в искусственных языках логики в удобном для логического анализа виде: кратко и точно.
Рассмотрим на примере, как, анализируя с помощью таблиц истинности логическую формулу сложного высказывания, выявляют условия его истинности, или, другими словами, как проводится табличное исследование логической формы высказывания на истинность.
В формуле p 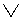 q
q  r три разных пропозициональных символа, у каждого из которых может быть одно из двух истинностных значений - либо истина, либо ложь. Рассчитаем, пользуясь правилом комбинаторики, количество сочетаний этих значений для трех символов: 23=8. Это значит, что в нашей таблице будет восемь строк. При двух пропозициональных символах было бы всего четыре строки (22=4).
r три разных пропозициональных символа, у каждого из которых может быть одно из двух истинностных значений - либо истина, либо ложь. Рассчитаем, пользуясь правилом комбинаторики, количество сочетаний этих значений для трех символов: 23=8. Это значит, что в нашей таблице будет восемь строк. При двух пропозициональных символах было бы всего четыре строки (22=4).
Теперь приступим к построению таблицы, записывая значения символов в столбец под каждым из них:
| р | 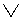 |
q |  |
r |
| 0 0 0 0 1 1 1 1 |
0 0 1 1 0 0 1 1 |
0 1 0 1 0 1 0 1 |
Следует обратить внимание на алгоритм перебора сочетаний: под первым символом пишем четыре раза "0" и четыре раза "1", под вторым - попарно "0" и "1", под третьим - попеременно "0" и "1". В результате ни одна из строк не повторяет другие и учтены все комбинации истинностных значений. Осталось провести исследование логических констант, содержащихся в формуле, в соответствии с их смысловыми значениями:
| р | 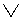 |
q |  |
r |
| 0 0 0 0 1 1 1 1 |
0 0 1 1 1 1 1 1 |
0 0 1 1 0 0 1 1 |
1 1 0 1 0 1 0 1 |
0 1 0 1 0 1 0 1 |
Истинность данной формулы определяется по предпоследнему столбцу. Мы видим, что не при всех сочетаниях истинностных значений пропозициональных символов в результате получается истина. При исследовании форм высказываний встречаются три варианта. Во-первых, формула, как в нашем случае, может оказаться выполнимой, т.е. имеются сочетания значений пропозициональных символов, приводящие к истине, но имеются и не приводящие к ней. Во-вторых, формула может оказаться тождественно-истинной (общезначимой, или законом символической логики). В этом случае при любом наборе значений переменных получается истина. В-третьих, формула может оказаться тождественно-ложной, т.е. при любом наборе значений переменных обращающейся в ложь.

Атрибутивные суждения. Переведем на язык логики предикатов суждения: «Иванов является смертным существом», «Все люди - смертные существа», «Ни один человек не является смертным существом», «Некоторые люди суть смертные существа», «Некоторые люди не суть смертные существа». Для этого заменим единичное имя «Иванов» символом а, общее имя «смертное существо» символом 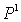 общее имя «человек» символом
общее имя «человек» символом 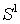 . Получим: «а суть
. Получим: «а суть 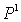 », «Все
», «Все 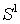 суть
суть 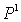 », «Ни один
», «Ни один 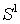 не есть
не есть 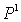 », «Некоторые
», «Некоторые 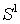 суть
суть 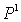 », «Некоторые
», «Некоторые 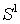 не суть
не суть 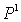 ». Переводом этих выражений на язык логики предикатов являются формулы:
». Переводом этих выражений на язык логики предикатов являются формулы:

(В тех случаях, когда местность предикатора можно установить по контексту, верхние индексы будем опускать.)
Эти формулы соответственно читаются: «а есть 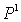 » (или
» (или 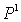 присуще а»), «для каждого х, если х есть
присуще а»), «для каждого х, если х есть 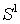 то х есть
то х есть 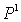 », «для каждого х, если х есть
», «для каждого х, если х есть 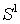 то неверно, что х есть
то неверно, что х есть 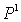 », «существует х такой, что x есть
», «существует х такой, что x есть 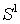 и х есть
и х есть 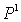 », «существует х такой, что х есть
», «существует х такой, что х есть 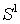 , и неверно, что х есть
, и неверно, что х есть 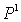 ».
».
Для нахождения способа перевода на язык логики предикатов суждений об отношениях воспользуемся знанием способа перевода атрибутивных суждений.
Предположим, что требуется перевести на язык логики предикатов суждение «Каждый юрист знает какого-нибудь (некоторого) логика». Истолкуем это суждение как атрибутивное. Тогда его можно выразить так: «Каждый юрист суть знающий некоторого логика». Заменим общие имена «юрист» и «знающий некоторого логика» символами S и Р. На языке логики предикатов имеем:  . Эта формула не полностью соответствует логической форме исходного суждения. Для полного выявления формы исходного суждения более полно выявим логическую форму выражения - «суть знающий некоторого логика». Заменим термин «знающий» символом
. Эта формула не полностью соответствует логической форме исходного суждения. Для полного выявления формы исходного суждения более полно выявим логическую форму выражения - «суть знающий некоторого логика». Заменим термин «знающий» символом  , а термин «логик» символом
, а термин «логик» символом  . Тогда это выражение можно записать так:
. Тогда это выражение можно записать так:
 а исходное суждение -
а исходное суждение -

Квантор существования можно вынести за внешнюю скобку:
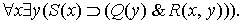
Формулами S(x), Q(y), R(x, у) заменяются предикаты «...суть юрист», «...суть логик», «...знает...», при этом вместо пустых мест ставятся индивидные переменные, указывающие области предметов, к которым предикаты применимы.
Исходя из сказанного, можно описать стандартный способ перевода суждений об отношениях на язык логики предикатов. Он представляет собой следующую систему предписаний:
а) заменить единичные и общие имена индивидными константами и предикаторами соответственно;
б) заменить кванторные слова кванторами и выписать кванторы с относящимися к ним переменными в порядке вхождения кванторных слов в предложение, выражающее суждение;
в) выписать формулу, заменяющую первый (по смыслу) предикат, поставив перед ней левую скобку; если индивидная переменная формулы, заменяющей первый предикат, связана квантором общности, то поставить после нее знак импликации, если же она связана квантором существования, то поставить после нее знак конъюнкции; после знака импликации или знака конъюнкции поставить левую скобку;
г) если индивидная переменная формулы, заменяющей второй(по смыслу) предикат, связана квантором общности, то выписать ее и поставить после нее знак импликации, если же она связана квантором существования, то выписать ее и поставить после нее знак конъюнкции; после знака импликации или знака конъюнкции поставить левую скобку (если переводится суждение о более чем двухместном отношении) и т.д.;
д) выписать формулу, заменяющую последний предикат;
е) после формулы, заменяющей последний предикат, поставить необходимое число правых скобок (если выявляется логическая форма отрицательного суждения, то перед последним предикатором поставить знак отрицания).
Воспользуемся описанным способом для перевода на язык логики предикатов суждения «Некоторые юристы знают каждого логика лучше, чем каждого агронома».
Заменим термины «юрист», «знающий лучше, чем», «логик», «агроном» соответственно символами  .
.
На языке логики предикатов это суждение выражается формулой:  .
.
Перевод на язык логики предикатов сложных суждений не связан с принципиальными дополнительными трудностями.
Пусть требуется выразить на языке логики предикатов, обогащенном символами  , суждение «Если необходимо, что все люди смертны, то необходимо, что некоторые люди смертны».
, суждение «Если необходимо, что все люди смертны, то необходимо, что некоторые люди смертны».
Для перевода этого суждения нужно сначала перевести составляющие его простые суждения. Заменив термины «человек» и «смертный» символами «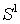 » и «
» и «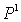 », получим:
», получим:

Антецедент и консеквент соответственно выражаются формулами:

В результате получим формулу, соответствующую исходному суждению 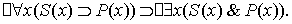
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про язык логики предикатов Надеюсь, что теперь ты понял что такое язык логики предикатов, логика предикатов, предикат и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Логика
Комментарии
Оставить комментарий
Логика
Термины: Логика