Лекция
Сразу хочу сказать, что здесь никакой воды про умозаключение, и только нужная информация. Для того чтобы лучше понимать что такое умозаключение, абстрактная мысль, вывод из посылки заключения , настоятельно рекомендую прочитать все из категории Логика.
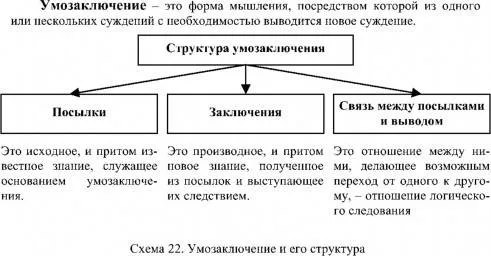
Самой развитой из основных форм абстрактного мышления является умозаключение - абстрактная мысль , в которой из посылки (исходного суждения) выводится заключение (новое суждение). Выводом называется логический переход от посылки к заключению.
Умозаключение — шаг логического вывода, непосредственное выведение высказывания-заключения из одного или более высказываний («посылок»), простейшее рассуждение.
В логике умозаключение записывается в виде горизонтальной черты, над которой стоят посылки, а под чертой записывается заключение. Например,
Все люди смертны.
Все греки — люди.
Все греки смертны
Умозаключения (отдельные шаги вывода) разделяют:
Умозаключение служит для расширения знаний: правила вывода формулируются так, чтобы исходная истина привела к новой. Следует помнить, что, если посылка содержит какую-то ложь, никакие правила логики не могут гарантировать истинность заключения. В этом случае вывод теряет практический смысл, ибо успешная практика возможна лишь на основе истинного знания о мире.
Согласно данному выше определению, любое умозаключение можно записать в виде простенькой схемы:
П
---.
З
Здесь П - посылка, З - заключение, а черта обозначает вывод (читается: "следовательно").
Откуда же берется огромное разнообразие умозаключений, если все они подчиняются простой трехчленной схеме? Дело в том, что, во-первых, посылка и заключение могут представлять собой не простое, а сложное суждение, иногда многозвенный комплекс суждений, а во-вторых - вывод может проводиться по разным правилам.
Существуют два типа вывода: достоверный и правдоподобный (первый гарантирует истинность заключения при истинных посылках, второй - нет). Отсюда вытекает деление умозаключений на достоверные и правдоподобные.
Ранее было принято сходу выделять не два, а три типа вывода: дедукцию (переход от общего знания о предмете к частному), индукцию (переход от частного знания к общему) и аналогию (перенос знания об одном предмете на другой). Соответственно получалось три типа умозаключений: дедуктивные, индуктивные и по аналогии. Как это традиционное трехчленное деление умозаключений соотносится с приведенным выше двучленным?
Все дедуктивные умозаключения - достоверные, и понятно почему: если истинно общее знание (знание о всех элементах данного множества), то истинно и частное знание (знание о части элементов множества). А вот умозаключения с индукцией и аналогией, как правило, - правдоподобные, так как, во-первых, истинное знание о некоторых элементах множества может оказаться ложным для остальных элементов, и, во-вторых, предмет, которому по аналогии приписаны свойства другого предмета, может не иметь этих свойств. Исключение из правила: умозаключение с полной обобщающей индукцией (о нем будет сказано ниже) является достоверным.
Основное внимание мы уделим дедуктивным умозаключениям, так как в силу своей достоверности они традиционно пользуются наибольшим уважением со стороны представителей формальной логики. При этом будут рассмотрены самые простые дедуктивные схемы.
Прежде всего обратимся к непосредственным умозаключениям, т.е. к тем, в которых вывод представляет собой преобразование единственной посылки, являющейся категорическим суждением. Здесь три основных вида: вывод по "логическому квадрату", обращение и превращение.
Вывод по "логическому квадрату" применяют для общего суждения - утвердительного или отрицательного. При этом движутся сверху вниз по вертикали "логического квадрата", т.е. переходят к соответствующему посылке частному суждению. Пример:
Всякий карп есть рыба.
________________________
Некоторые карпы суть рыбы.
Теперь о правилах обращения. Основное правило очень простое: при обращении меняют местами субъект и предикат посылки. Но помимо этого правила нужно помнить о двух ограничениях: во-первых, общее утверждение заменяют частным, а во-вторых - для частноотрицательного суждения обращение не проводят. Пример:
Всякий карп есть рыба.
--------------------
Некоторые рыбы суть карпы.
Правило превращения: качество посылки меняют на противоположное, а ее предикат берут с отрицанием. Пример:
Всякий карп есть рыба.
--------------------
Ни один карп не есть не-рыба.
Здесь несколько подгрупп:
Modus ponens (утверждающее условно-категорическое умозаключение):
А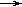 В, А
В, А
____________
В
Пример: "Если этот газ неон, то он инертный. Этот газ неон. Следовательно, он инертный".
Modus tollens (отрицающее условно-категорическое умозаключение):
А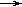 В,
В, 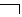 В
В
___________
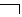 А
А
Пример: "Если этот газ неон, то он инертный. Этот газ не инертный. Следовательно, это не есть неон".
Modus ponendo-tollens (утверждающе-отрицающее разделительно-категорическое умозаключение). Эта схема имеет два варианта:
| 1)
|
А |
2)
|
А |
Пример (для первого варианта): "Или я дома, или я вне дома. Я дома. Следовательно, не верно, что я вне дома".
Modus tollendo-ponens (отрицающе-утверждающее разделительно-категорическое умозаключение). У этой схемы тоже два варианта:
| 1)
|
А |
2)
|
А |
Запись "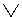 (
(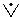 )" означает, что схема годится для любой дизъюнкции - и строгой, и нестрогой. Пример (для первого варианта, с нестрогой дизъюнкцией): "Идет дождь или снег. Дождь не идет. Следовательно, идет снег".
)" означает, что схема годится для любой дизъюнкции - и строгой, и нестрогой. Пример (для первого варианта, с нестрогой дизъюнкцией): "Идет дождь или снег. Дождь не идет. Следовательно, идет снег".
Дилеммы бывают четырех видов:
|
Дилемма |
конструктивная |
деструктивная |
|
простая |
A |
A |
|
сложная |
A |
A |
Пример сложной конструктивной дилеммы: "Если на улице дождь, то мокро, если гололед, то скользко. На улице дождь или гололед. Следовательно, мокро или скользко".
1) Контрапозиция:
А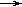 В
В
_______
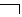 В
В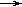
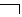 A
A
Пример: "Если идет дождь, то на улице мокро. Следовательно, если на улице не мокро, то не идет дождь".
2) Сложная контрапозиция:
А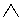 B
B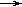 C
C
________
A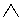
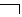 C
C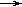
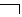 B
B
Пример: "Если утюг исправный и включен в работающую сеть, то он нагревается. Следовательно, если утюг исправный и не нагревается, то он не включен в работающую сеть".
3) Транзитивность:
А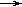 В, B
В, B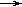 C
C
_________
А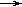 C
C
Пример: "Если данное число три, то оно больше двух. Если данное число больше двух, то оно больше одного. Следовательно, если данное число три, то оно больше одного".
4) Экспортация:
А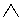 B
B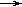 C
C
_____
A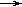 (B
(B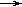 C)
C)
Пример: "Если дело знакомое и интересное, то оно ладится. Следовательно, если дело знакомое, то, если оно интересное, оно ладится".
5) Импортация:
A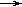 (B
(B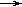 C)
C)
______
А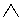 B
B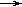 C
C
Чтобы привести пример импортации, можно взять предыдущий пример, поменяв местами посылку и заключение.
Последний класс дедуктивных умозаключений, о котором следует знать в рамках данного курса логики, - простой категорический силлогизм, т.е. умозаключение, состоящее из трех категорических суждений: двух посылок и заключения. Это умозаключение включает в себя три понятия, каждое из которых используется дважды. Их называют терминами силлогизма (два крайних - меньший и больший - и средний термины) и обозначают латинскими буквами S, P и М.
Откуда взялись такие обозначения и как находить термины силлогизма? Рассмотрим классический пример, который гуляет по учебникам логики еще с дореволюционных времен: "Все люди смертны. Сократ человек. Следовательно, Сократ смертен". Записав все суждения и весь силлогизм строго стандартно, получим следующую форму:
Всякий человек есть смертный.
Сократ есть человек.
___________________
Сократ есть смертный.
Логический анализ конкретного силлогизма лучше всего начинать с заключения. Дело в том, что в заключении правильно составленного простого категорического силлогизма меньший термин всегда играет роль субъекта, а больший - предиката. Отсюда и буквы для крайних терминов - S и Р. В данном примере S - Сократ, Р - смертное (существо). Ну, а в качестве термина М (от латинского слова "medius" - "средний") здесь фигурирует понятие человека.
По расположению терминов различают фигуры простого категорического силлогизма. Всего их четыре, обозначают их римскими цифрами:
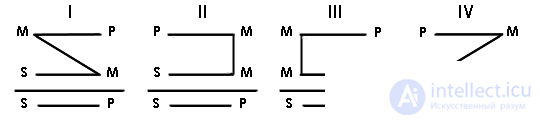
У каждой фигуры есть модусы - формы, определяемые по видам категорических суждений, из которых состоит силлогизм. Причем виды суждений нужно определять строго последовательно, продвигаясь сверху вниз по схеме фигуры. Например, модус EIO имеет место тогда, когда бoльшая (верхняя на схеме) посылка относится к виду Е, меньшая - к виду I, а заключение - к виду О. Что касается умозаключения про Сократа, то это - модус ААА I фигуры.
Для каждой фигуры выявлен набор правильных модусов, т.е. тех, которые гарантируют истинность заключения при истинных посылках. Вот эти модусы:
| I | II | III | IV |
| AAA | AEE | AAI | AAI |
| EAE | AOO | EAO | AEE |
| AII | EAE | IAI | IAI |
| EIO | EIO | OAO | EAO |
| AII | EIO | ||
| EIO |
Знание правильных модусов помогает быстро определить истинность силлогизма. Например, выяснив, что умозаключение про Сократа имеет истинные посылки и что оно относится к модусу ААА I фигуры простого категорического силлогизма, т.е. к одному из правильных модусов этой фигуры, можно не сомневаться, что данное рассуждение истинное.
Теперь несколько слов про умозаключения с индукцией и аналогией. Что касается первых, то здесь основной вид - неполная обобщающая индукция. Если {К} - интересующее нас множество, {S} - подмножество этого множества, Si - элемент подмножества {S}, Р - интересующий нас признак, то схема этого вида индуктивных умозаключений будет выглядеть так:
S1 - P
S2 - P
…
Sn - P
{S1, S2, …, Sn} = {S}
_______________
Возможно, {К} - Р
Пример: мне захотелось выяснить, обладает ли множество учебников ({К}) признаком "быть имеющим твердую обложку" (Р). Множество учебников - очень большое, поэтому я ограничился исследованием подмножества "учебник моей домашней библиотеки" ({S}). Все книги этого подмножества оказались в твердой обложке. Делаю индуктивное заключение: "Возможно, всякий учебник имеет твердую обложку". Слово "возможно" говорит о том, что вывод не исключает ошибку. И она явно присутствует в проведенном мною индуктивном исследовании: почему бы учебнику не быть в мягкой обложке?
Если бы меня интересовало только множество учебников моей домашней библиотеки, то мой вывод оказался бы достоверным. Это была бы полная обобщающая индукция:
S1 - P
S2 - P
…
Sn - P
{S1, S2, …, Sn} = {S}
---------
{S} - Р
Умозаключением по аналогии называется такое умозаключение, в котором на основании сходства двух предметов в некоторых свойствах делают заключение об их сходстве и в других свойствах. Пусть схожие предметы - R1 и R2, а свойства предметов - a, b, c и d. Тогда схему умозаключения по аналогии можно записать так:
R1 - a, b, c, d
R2 - a, b, c
---------
Возможно, R2 - d.
Классический пример - возникновение гипотезы о наличии жизни на Марсе. Наблюдая Марс в телескопы, астрономы обнаружили большое сходство с Землей. Поскольку на Земле имеется жизнь, предположили, что она есть и на Марсе. Эта гипотеза пока не нашла подтверждения.
Почему, несмотря на возможность ошибок, индукция и аналогия широко применяются на практике? Дело в том, что в серьезных исследованиях такие выводы используют не в чистом виде, а в сочетании с дедукцией.
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про умозаключение Надеюсь, что теперь ты понял что такое умозаключение, абстрактная мысль, вывод из посылки заключения и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Логика
Комментарии
Оставить комментарий
Логика
Термины: Логика