Переписывание (Система замены терминов) в математике , лингвистике , информатике и логике п

Привет, Вы узнаете о том , что такое переписывание, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое переписывание, система замены терминов , настоятельно рекомендую прочитать все из категории Логика.

В математике , лингвистике , информатике и логике переписывание охватывает широкий спектр методов замены подтермов формулы другими терминами. Такие методы могут быть реализованы с помощью систем переписывания (также известных как системы переписывания , механизмы переписывания или системы редукции ). В своей простейшей форме они состоят из набора объектов и отношений , определяющих , как эти объекты преобразуются.

Переписывание может быть недетерминированным . Одно правило переписывания термина может быть применено к нему множеством различных способов, или может быть применимо несколько правил. В таком случае системы переписывания предоставляют не алгоритм для замены одного термина другим, а набор возможных вариантов применения правил. Однако в сочетании с соответствующим алгоритмом системы переписывания можно рассматривать как компьютерные программы , и некоторые программы доказательства теорем и декларативные языки программирования основаны на переписывании терминов.

Переписывание — широкий спектр техник, методов и теоретических результатов, связанных с процедурами последовательной замены частей формул или термов формального языка по заданной схеме — системе переписывающих правил. В наиболее общей форме речь идет о совокупности некоторого набора объектов и правил — отношений между этими объектами, которые указывают как преобразовать этот набор.

Переписывание может быть недетерминированным. Например, система переписывающих правил может включать в себя правило, которое может быть применено к одному и тому же терму несколькими разными способами, но не содержать, при этом, указания на то, какой конкретно способ нужно применить в том или ином случае. Если система переписывания, все же, оформлена в качестве однозначно понимаемого алгоритма, она может рассматриваться как компьютерная программа. На техниках переписывания основан ряд систем интерактивного доказательства теорем и декларативных языков программирования .

В логике процедура получения конъюнктивной нормальной формы (КНФ) формулы может быть реализована как система переписывания. [ 6 ] Например, правила такой системы будут следующими:

( устранение двойного отрицания )

( Законы Де Моргана )

( распределительность )

Для каждого правила каждая переменная обозначает подвыражение, а символ ( ) означает, что выражение, соответствующее левой части, можно переписать в выражение, соответствующее правой части. В такой системе каждое правило является логической эквивалентностью , поэтому переписывание выражения по этим правилам не меняет его истинностного значения. Другие полезные системы переписывания в логике могут не сохранять истинностные значения, см., например, равновыполнимость .

Системы переписывания термов могут использоваться для вычисления арифметических операций над натуральными числами . Для этого каждое такое число должно быть закодировано как терм . Простейшая кодировка используется в аксиомах Пеано и основана на константе 0 (нуле) и функции следования S. Например, числа 0, 1, 2 и 3 представлены термами 0, S(0), S(S(0)) и S(S(S(0))) соответственно. Следующая система переписывания термов может затем использоваться для вычисления суммы и произведения заданных натуральных чисел.

Например, вычисление 2+2, дающее в результате 4, можно продублировать, переписав термин следующим образом:

→(2) →(2)

где обозначение над каждой стрелкой указывает правило, используемое для каждой перезаписи.

В качестве другого примера, вычисление 2⋅2 выглядит так:

→са

где последний шаг включает в себя вычисления предыдущего примера.

В лингвистике правила построения фраз , также называемые правилами переписывания , используются в некоторых системах генеративной грамматики [ 8 ] как средство создания грамматически правильных предложений языка. Такое правило обычно имеет вид , где A — метка синтаксической категории , например, именная группа или предложение , а X — последовательность таких меток или морфем , выражающая тот факт, что A может быть заменено на X при формировании структуры предложения. Об этом говорит сайт https://intellect.icu . Например, правило означает, что предложение может состоять из именной группы (NP), за которой следует глагольная группа (VP); дальнейшие правила укажут, из каких подкомпонентов может состоять именная группа и глагольная группа, и т. д.

Из приведенных выше примеров ясно, что мы можем рассматривать системы переписывания абстрактно. Нам необходимо указать набор объектов и правила, которые могут применяться для их преобразования. Наиболее общая (одномерная) реализация этого понятия называется абстрактной системой редукции [ 9 ] или абстрактной системой переписывания (сокращенно ARS ). [ 10 ] ARS — это просто набор A объектов вместе с бинарным отношением → на A , называемым отношением редукции , отношением переписывания [ 11 ] или просто редукцией . [ 9 ]

Многие понятия и обозначения могут быть определены в общей настройке ARS.→∗является рефлексивным транзитивным замыканием→.↔является симметричным замыканием→.↔∗является рефлексивным транзитивным симметричным замыканием→. Текстовая задача для ARS заключается в определении, по заданным x и y , является лих↔∗уОбъект x в A называется приводимым , если существует некоторый другой y в A , такой чтох→у; в противном случае он называется неприводимым или нормальной формой . Объект y называется «нормальной формой x », еслих→∗у, и y неприводим. Если нормальная форма x единственна, то это обычно обозначается какх↓. Если каждый объект имеет хотя бы одну нормальную форму, ARS называется нормализующей .х↓уили x и y называются соединяемыми, если существует некоторый z со свойством, что . Говорят, что ARS обладает свойством Черча-Россера, еслих↔∗уподразумеваетх↓у. ARS является конфлюэнтным, если для всех w , x и y в A , подразумеваетх↓у. ARS локально конфлюэнтна тогда и только тогда, когда для всех w , x и y в A , х←в→уподразумеваетх↓у. ARS называется терминальной или нетеровой, если не существует бесконечной цепи Сливающаяся и завершающаяся АРС называется конвергентной или канонической .

Важные теоремы для абстрактных переписывающих систем заключаются в том, что ARS является конфлюэнтным тогда и только тогда, когда она обладает свойством Черча-Россера, лемме Ньюмена (концевая ARS является конфлюэнтной тогда и только тогда, когда она локально конфлюэнтна), и что проблема тождества слов для ARS в общем случае неразрешима .

Система перезаписи строк (SRS), также известная как полусистема Туэ , использует свободную моноидную структуру строк ( слов) над алфавитом для расширения отношения перезаписи,Р, ко всем строкам в алфавите, содержащим левую и правую части некоторых правил в качестве подстрок . Формально полусистема Туэ представляет собой кортеж (Σ,Р)гдеΣпредставляет собой (обычно конечный) алфавит, иР— это бинарное отношение между некоторыми (фиксированными) строками в алфавите, называемое набором правил перезаписи . Отношение перезаписи за один шаг →РвызванныйРнаΣ∗определяется как: еслис, есть какие-то строки, тогда если существуют такой что , , итыРв. С→Рэто отношение наΣ∗, пара(Σ∗,→Р)Подходит под определение абстрактной системы переписывания. Поскольку пустая строка находится в ,Рявляется подмножеством→Р. Если отношениеРсимметрична , то система называется системой Туэ .

В SRS отношение редукции совместимо с моноидной операцией, что означает, чтох→Р∗уподразумеваеттыхв→Р∗тыувдля всех строкх,у,ты,в∈Σ∗. Аналогично, рефлексивное транзитивное симметричное замыкание , обозначенный , является конгруэнтностью , то есть отношением эквивалентности (по определению), а также совместимо с конкатенацией строк. Отношение↔Р∗называется конгруэнтностью Туэ, порожденной . В системе Туэ, т.е. еслиРсимметрично, переписываемое соотношение→Р∗совпадает с конгруэнтностью Туэ↔Р∗.

Понятие полусистемы Туэ по сути совпадает с представлением моноида . Поскольку↔Р∗является конгруэнтностью, мы можем определить фактор-моноид МР=Σ∗/↔Р∗свободного моноидаΣ∗по сравнению с Туэ. Если моноидМизоморфен с​ , то полусистема Туэ(Σ,Р)называется моноидным представлениемМ.

Мы сразу же обнаруживаем очень полезные связи с другими разделами алгебры. Например, с алфавитом. с правилами , гдеεпустая строка , это представление свободной группы на одном генераторе. Если же вместо этого правила просто , то мы получаем представление бициклического моноида . Таким образом, полусистемы Туэ представляют собой естественную основу для решения проблемы тождества слов для моноидов и групп. Фактически, каждый моноид имеет представление вида(Σ,Р), т. е. он всегда может быть представлен полусистемой Туэ, возможно, над бесконечным алфавитом.

Проблема слов для полусистемы Туэ в общем случае неразрешима; этот результат иногда называют теоремой Пост-Маркова . [ 12 ]

Рис.1: Схематическая треугольная диаграмма применения правила перезаписи в позициипв термине, с соответствующей заменойσ

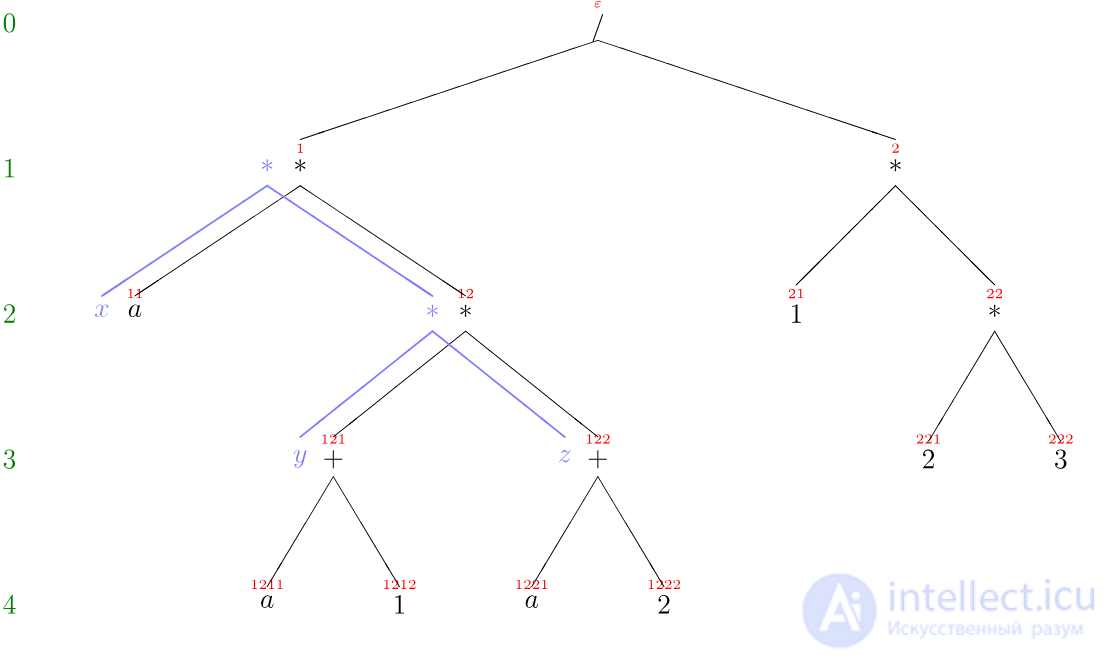
Рис.2: Правило левого термина соответствие в терминах

Система переписывания терминов ( TRS ) — это система переписывания, объектами которой являются термины , то есть выражения с вложенными подвыражениями. Например, система, показанная выше в разделе «Логика», является системой переписывания терминов. Термы в этой системе состоят из бинарных операторов.(∨)и(∧)и унарный оператор(¬). В правилах также присутствуют переменные, которые представляют любой возможный термин (хотя одна переменная всегда представляет один и тот же термин в одном правиле).

В отличие от систем перезаписи строк, объектами которых являются последовательности символов, объекты системы перезаписи термов образуют алгебру термов . Терм можно представить в виде дерева символов, при этом множество допустимых символов фиксируется заданной сигнатурой . Как формализм, системы перезаписи термов обладают всей мощью машин Тьюринга , то есть каждая вычислимая функция может быть определена системой перезаписи термов. [ 13 ]

Некоторые языки программирования основаны на переписывании терминов. Одним из таких примеров является Pure, функциональный язык программирования для математических приложений.

Правило перезаписи представляет собой пару терминов , обычно записываемых какл→р, чтобы указать, что левую часть l можно заменить правой частью r . Система переписывания термов — это набор R таких правил. Правилол→рможет быть применен к термину s, если левый термин l совпадает с некоторым подтермом s , то есть, если есть некоторая замена σтаким образом, что подтерминсукорененный в некоторой позиции p, является результатом применения заменыσк термину l . Подтермин, соответствующий левой части правила, называется редексом или приводимым выражением . [ 16 ] Результирующий термин t применения этого правила является результатом замены подтермина в позиции p в s термином рс заменойσприменяется, см. рисунок 1. В этом случае,сговорят, что он переписывается за один шаг или переписывается напрямую ,тсистемойР, формально обозначаемый какс→Рт,с→Рт, или какс→Ртнекоторыми авторами.

Если терминт1можно переписать в несколько этапов в терминтн, то есть, еслит1→Рт2→Р⋯→Ртн, терминт1говорят, что переписывается натн, формально обозначаемый какт1→Р+тн. Другими словами, отношение→Р+является транзитивным замыканием отношения→Р; часто также обозначение→Р∗используется для обозначения рефлексивно-транзитивного замыкания→Р, то есть еслис=тилис→Р+т Переписывание термина , заданное наборомРправил можно рассматривать как абстрактную систему переписывания, как определено выше , с терминами в качестве ее объектов и→Ркак его переписывающее отношение.

Например, это правило перезаписи, обычно используемое для установления нормальной формы относительно ассоциативности∗Это правило можно применить к числителю в члене с соответствующей заменой , см. рисунок 2. Применение этой замены к правой части правила дает термин , и замена числителя этим членом дает , что является результатом применения правила перезаписи. В целом, применение правила перезаписи позволило достичь того, что называется «применением закона ассоциативности для "в элементарной алгебре. Альтернативно, правило можно было бы применить к знаменателю исходного члена, получив .

Вопросы завершения работы систем перезаписи в целом рассматриваются в разделе «Аннотация системы перезаписи#Окончание и сходимость» . Для систем перезаписи терминов в частности следует учитывать следующие дополнительные тонкости.

Завершение даже системы, состоящей из одного правила с линейной левой частью, неразрешимо. Завершение также неразрешимо для систем, использующих только унарные функциональные символы; однако оно разрешимо для конечных базовых систем.

Следующая система перезаписи терминов является нормализующей, , но не завершающей, и не конфлюэнтной:

Следующие два примера систем перезаписи терминов относятся к Тояме:

и

г(х,у)→х,

г(х,у)→у.

Их союз – это система, не подлежащая расторжению, поскольку

Этот результат опровергает предположение Дершовица [ 23 ] , который утверждал , что объединение двух систем перезаписи терминовР1иР2снова завершается, если все левые частиР1и правые стороныР2линейны , и нет никаких « наложений » между левыми частямиР1и правые стороныР2Всем этим свойствам удовлетворяют примеры Тоямы.

См. разделы Порядок перезаписи и Порядок пути (перезапись терминов) для получения информации об отношениях упорядочивания, используемых в доказательствах завершения для систем перезаписи терминов.

Системы переписывания высшего порядка являются обобщением систем переписывания членов первого порядка до лямбда-термов , что позволяет использовать функции высшего порядка и связанные переменные. Различные результаты о TRS первого порядка можно переформулировать и для HRS. [ 25 ]

Системы перезаписи графов являются еще одним обобщением систем перезаписи терминов, оперирующих графами вместо ( основных ) терминов / их соответствующего древовидного представления.

Теория трассировки предоставляет средства для обсуждения многопроцессорной обработки в более формальных терминах, например, через моноид трассировки и моноид истории . Перезапись также может выполняться в системах трассировки.

Несмотря на то, что изначально понятие переписывания было введено для лямбда-исчисления, основной массив результатов и приложений в настоящее время касается переписывания первого порядка. Переписывающие системы такого рода называют Системами Переписывания Термов или TRS (от англ. Term rewriting systems).

Системы переписывания высших порядков являются обобщением систем переписывания термов первого порядка на лямбда-термы, позволяя функции высших порядков и связанные переменные. Различные результаты о системах переписывания термов первого порядка также могут быть переформулированы для высших порядков.^[

• Критическая пара ( логика )
• Компилятор
• Алгоритм завершения Кнута-Бендикса
• L- системы определяют перезапись, которая выполняется параллельно.
• Ссылочная прозрачность в информатике
• Регулируемое переписывание
• Сети взаимодействия
• Лямбда-исчисление
• Переписывающая система
• Представление группы
• Рефал

Исследование, описанное в статье про переписывание, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое переписывание, система замены терминов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Логика

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.