Лекция
Привет, Вы узнаете о том , что такое способы доказательства, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое способы доказательства, прямое доказательство, косвенное доказательство, апагогическое доказательство, апагогическое доказательство , настоятельно рекомендую прочитать все из категории Логика.
Обычно доказательство слагается из серии шагов. Нужно уметь проследить каждый шаг доказательства, иначе его части лишатся связи, и оно в любой момент может рассыпаться, как карточный домик. Но не менее важно понять доказательство в целом, как единую конструкцию, каждая часть которой необходима на своем месте.
Доказательство, не понятое как целое, ни в чем не убеждает. Даже если выучить его наизусть, предложение за предложением, к имеющемуся знанию предмета это ничего не прибавит. Следить за доказательством и лишь убеждаться в правильности каждого его последующего шага — это равносильно такому наблюдению за игрой в шахматы, когда замечаешь только то, что каждый ход подчинен правилам игры.
Минимальное требование — это понимание логического выведения как целенаправленной процедуры. Только в этом случае достигается интуитивная ясность того, что мы делаем.
То, что создает «единство доказательства», можно представить в форме общей схемы, охватывающей основные его шаги, воплощающей в себе сто принцип или его итоговую структуру. Именно такая схема остается в памяти, когда забываются подробности доказательства.
Доказательства делятся на прямые и косвенные.

С точки зрения общего движения мысли все доказательства подразделяются на прямые икосвенные.
При прямом доказательстве задача состоит в том, чтобы подыскать такие убедительные аргументы, из которых по логическим правилам получается тезис.
Например, нужно доказать, что сумма углов четырехугольника равна 360°С. Из каких утверждений можно было бы вывести этот тезис? Отмечаем, что диагональ делит четырехугольник на два треугольника. Значит, сумма его углов равна сумме углов двух треугольников. Известно, что сумма углов треугольника составляет 180°С. Из этих положений выводим, что сумма углов четырехугольника равна 360°С.
В построении прямого доказательства можно выделить два связанных между собой этапа: отыскание тех признанных обоснованными утверждений, которые способны быть убедительными аргументами для доказываемого положения; установление логической связи между найденными аргументами и тезисом. Нередко первый этап считается подготовительным, и под доказательством понимается дедукция, связывающая подобранные аргументы и доказываемый тезис.
Еще пример. Нужно доказать, что космические корабли подчиняются действию законов небесной механики. Известно, что эти законы универсальны: им подчиняются все тела в любых точках космического пространства. Очевидно также, что космический корабль есть космическое тело. Отметив это, строим соответствующее дедуктивное умозаключение. Оно является прямым доказательством рассматриваемого утверждения.

В прямом доказательстве тезис непосредственно обосновывается аргументами. Например, тезис «Некоторые писатели — авторы детективных произведений» обосновывается аргументами: «Артур Конан Дойл — автор детективных произведений» (ai), «Агата Кристи — автор детективных произведений» (а2), «Юлиан Семенов — автор детективных произведений» (а3). Этих аргументов достаточно для обоснования истинности тезиса. Демонстрация принимает форму утверждающего модуса условно-категорического умозаключения:
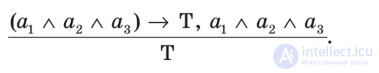
Из истинности оснований следует истинность тезиса.

Рис. Об этом говорит сайт https://intellect.icu . 32. Т — тезис, а, а2 ... ап — аргументы, Т — связь тезиса с аргументами (аргументация)
Прямое доказательство представлено на рис. 32.
Косвенное доказательство устанавливает справедливость тезиса тем, что вскрывает ошибочность противоположного ему допущения (антитезиса).
Как с иронией замечает математик Д. Пойа, «косвенное доказательство имеет некоторое сходство с надувательским приемом политикана, поддерживающего своего кандидата тем, что опорочивает репутацию кандидата другой партии». В косвенном доказательстве рассуждение идет как бы окольным путем. Вместо того чтобы прямо отыскивать аргументы для выведения из них доказываемого положения, формулируется антитезис, отрицание этого положения. Далее тем или иным способом показывается несостоятельность антитезиса. По закону исключенного третьего, если одно из противоречащих друг другу утверждений ошибочно, второе должно быть верным. Антитезис ошибочен, значит, тезис верен.
Поскольку косвенное доказательство использует отрицание доказываемого положения, оно является, как говорят, доказательством от противного.
Допустим, нужно построить косвенное доказательство такого весьма тривиального тезиса: «Квадрат не является окружностью». Выдвигается антитезис: «Квадрат есть окружность». Необходимо доказать ложность этого утверждения. С этой целью выводим из него следствия. Если хотя бы одно из них окажется ложным, это будет означать, что и само утверждение, из которого выведено следствие, также ложно. Неверно, в частности, такое следствие: у квадрата нет углов. Поскольку антитезис ложен, исходный тезис должен быть истинным.
Другой пример. Врач, убеждая пациента, что тот не болен гриппом, рассуждает так. Если бы действительно был грипп, имелись бы характерные для него симптомы: головная боль, повышенная температура и т.п. Но ничего подобного нет. Значит, нет и гриппа.
Это опять-таки косвенное доказательство. Вместо прямого обоснования тезиса выдвигается антитезис, что у пациента, в самом деле, грипп. Из антитезиса выводятся следствия, но они опровергаются объективными данными. Это говорит, что допущение о гриппе неверно. Отсюда следует, что тезис «Гриппа нет» истинен.
Доказательства от противного обычны в наших рассуждениях, особенно в споре. При умелом применении они могут обладать особенной убедительностью.

Косвенное доказательство делится на: 1) апагогическое и 2) разделительное.
1. В апагогическом (от греч. apagogos — уводящий, отводящий) косвенном доказательстве истинность тезиса обосновывается путем доказательства ложности антитезиса.
Важно подчеркнуть, что антитезис (АТ) — это суждение, противоречащее тезису . Доказательство строится в следующей последовательности.
1. Формулируем антитезис. По отношению к тезису «Некоторые писатели — авторы детективных произведений» (Т), выраженного частноутвердительным суждением (/), антитезис выражается общеотрицательным суждением (Е):
«Ни один писатель не является автором детективных произведений» (АТ).
2. Из антитезиса, условно принятого за истинный, выводим логические следствия:
3. Сопоставляем следствия с фактами, устанавливаем ложность следствий: все указанные писатели — авторы детективных произведений.
Прием выведения следствий из антитезиса, оказавшихся ложными, называется приведением к абсурду (приведением к нелепости).
4. Из ложности следствий вытекает ложность антитезиса, т. е.
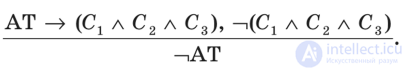
5. Из ложности антитезиса (АТ) следует истинность тезиса (Т):
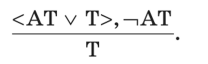
Тезис доказан.
Схема апагогического косвенного доказательства приведена на рис. 33.
В разделительном косвенном доказательстве обоснование тезиса, который выступает членом разделительного (дизъюнктивного) суждения, устанавливается путем установления ложности всех других его членов. Например, формулируя предположение о причине возникновения пожара на складе в результате неосторожного обращения с огнем (Т), выдвигаем другие версии: поджог (А), неисправность электропроводки (Б).

Рис. 33
Если в ходе расследования предположения о поджоге и неисправности электропроводки не подтвердились, остается одна причина — неосторожное обращение с огнем, т. е.
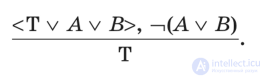
Доказательство построено по отрицающе-утвер- ждающему модусу разделительно-категорического умозаключения. Однако тезис будет доказан при условии соблюдения правила этого модуса: разделительная посылка должна быть суждением полной дизъюнкции. В данном случае это значит, что другие причины пожара исключаются.
1. Подберите аргументы, постройте прямое доказательство тезиса.
Образец
Все дни на прошлой неделе были дождливыми (Т). Приводим аргументы.
В понедельник шел дождь (ai). Во вторник шел дождь (а2). Дождь шел в среду, четверг и пятницу (a3, а4, а5). Дождь шел и в остальные два дня недели (а6, а7).
Построив демонстрацию в форме полной индукции, получим достоверный вывод. Тезис доказан, (яь —> Т.
2. Подберите аргументы, постройте косвенное апагогическое доказательство тезиса упражнения 1.
Образец
Все дни на прошлой недели были дождливыми (Т).
3. Постройте косвенное разделительное доказательство.
Образец
Швейцария — конфедеративное государство (Т). Аргументы:
По форме государственного устройства государство может быть конфедеративным (Т), унитарным (Ai) или федеративным (А2). Швейцария не унитарное (—iAj) и не федеративное (—iА2) государство.
Из ложности тезисов А и А2 с необходимостью следует истинность тезиса (Т), т. е.:
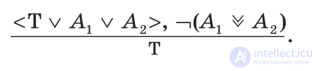
1. Востоков получил на экзамене оценку «отлично».
2. Он студент заочного отделения.
3. Чугунов участвовал в преступлении как организатор.
1. Какое доказательство называется прямым? Как оно строится?
2. Что такое апагогическое косвенное доказательство? На какие этапы делится его построение?
3. В форме какого умозаключения строится разделительное косвенное доказательство?
В общем, мой друг ты одолел чтение этой статьи об способы доказательства. Работы впереди у тебя будет много. Смело пиши комментарии, развивайся и счастье окажется в твоих руках. Надеюсь, что теперь ты понял что такое способы доказательства, прямое доказательство, косвенное доказательство, апагогическое доказательство, апагогическое доказательство и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Логика
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Логика
Термины: Логика