Лекция
Привет, сегодня поговорим про логические построения элементов, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое логические построения элементов , настоятельно рекомендую прочитать все из категории Компьютерная схемотехника и архитектура компьютеров.
В электронных вычислительных машинах ( ЭВМ) вся информация представлена на языке, содержащем всего два символа алфавита – 0 и 1. Элементы, выполняющие простейшие операции над такими символами, называются логическими. На основе логических элементов строятся узлы ЭВМ, предназначенные для выполнения всего многообразия более сложных операций, выполняемых ЭВМ.
Теоретической базой для построения узлов ЭВМ является алгебра логики, разработанная английским математиком Джорджем Булем и обычно называемаябулевой алгеброй. Для реализации какой-либо функции в виде узла ЭВМ на основе законов булевой алгебры разрабатывается логическое уравнение для этой функции, в соответствии с которым выбираются и соединяются между собой логические элементы.
Булева алгебра состоит из следующих элементов:
1. числа,
2. переменные,
3. операции,
4. выражения,
5. функции,
6. законы.
Рассмотрим каждый из представленных элементов:
1. Числа – два числа: логический ноль (лог. «0») и логическая единица (лог. «1») в Булевой алгебре отождествляются с понятиями «истина» и «ложь»;
2. Переменные – булевы (логические, двоичные) переменные называются переменными, принимающими значения из множества ноль и единица {0;1};
3. Операции – простейшие логические функции Булевой алгебры, в состав которых входят:
3.1. Отрицание (инверсия):
Только операция отрицания является унарной (операция с одной переменной). К примеру: операция 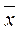 означает отрицание переменной
означает отрицание переменной 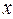 , т.е., при
, т.е., при 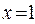
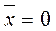 и наоборот – при
и наоборот – при 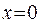
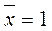 . Отрицание может быть применено и к выражению –
. Отрицание может быть применено и к выражению – 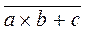 , т.к. выражение
, т.к. выражение 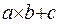 можно представить в виде функции
можно представить в виде функции 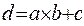 , то инверсия функции
, то инверсия функции 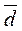 будет иметь следующий вид
будет иметь следующий вид 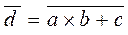 .
.
Операция отрицания (НЕ) f=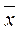 читается, как f есть (эквивалентна) НЕ
читается, как f есть (эквивалентна) НЕ 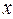 . Элемент, реализующий функцию НЕ, называется элементом НЕ (инвертором).
. Элемент, реализующий функцию НЕ, называется элементом НЕ (инвертором).

3.2. Конъюнкция (логическое умножение):
Операции конъюнкции и дизъюнкции выполняются над, как минимум, двумя переменными или одной переменной и константой.
Для написания операции конъюнкции применяются следующие символы (знакооперации): 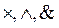 , а так же, как и при записи арифметического умножения, допускается опускание символа операции умножения. К примеру, записи:
, а так же, как и при записи арифметического умножения, допускается опускание символа операции умножения. К примеру, записи: 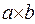 ,
, 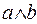 ,
, и
и 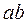 означают операцию конъюнкции над переменными
означают операцию конъюнкции над переменными 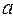 и
и 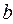 .
.
Операция конъюнкции (логического умножения) записывается в виде f=X1·X2. Функция конъюнкции читается так: f есть (эквивалентна) Х1 и Х2, поскольку функция истинна тогда, когда истинны 1-й и 2-й аргументы (переменные). Конъюнкциюназывают функцией И, а элемент, реализующий эту функцию, элементом И.
В общем случае функцию логического умножения от n переменных записывают так:
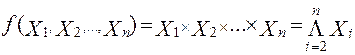


Количество переменных (аргументов), участвующих в одной конъюнкции, соответствует количеству входов элементаИ.
3.3. Дизъюнкция (логическое сложение):
Для написания операции дизъюнкции применяются следующие символы: 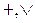 . К примеру, записи:
. К примеру, записи: 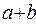 и
и 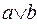 означают операцию дизъюнкции над переменными
означают операцию дизъюнкции над переменными 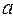 и
и 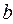 .
.
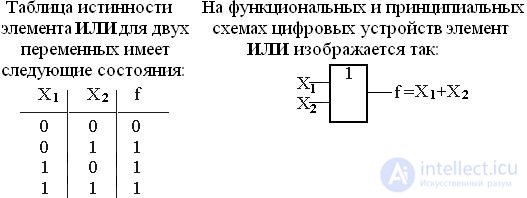
Дизъюнкция (логическое сложение) записывается в виде
f=X1 + X2, и читается так: f есть Х1 или Х2, поскольку функция истинна, когда истинна одна или другая переменная (хотя бы одна). Поэтому функцию дизъюнкции часто называют функцией ИЛИ.
В общем случае функцию логического сложения от n переменных записывают так:
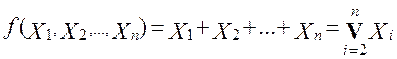

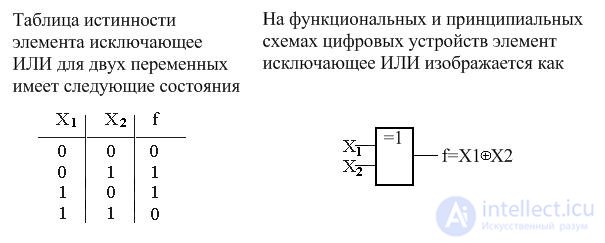
3.4. Исключающее ИЛИ ( сложение по модулю 2)
Для написания операции исключающего ИЛИ используют знак  .
.
Операция исключающего ИЛИ записывается как f=X1 X2 , и читается как f есть исключающее ИЛИ от X1 и X2, или f равно сумме по модулю 2 X1 и X2.
X2 , и читается как f есть исключающее ИЛИ от X1 и X2, или f равно сумме по модулю 2 X1 и X2.
4. Выражения – переменные и знакооперации, соединенные вместе при возможном наличии скобок для задания порядка выполнения операций. Приоритет задается порядком операции. У операции конъюнкции порядок выше, чем у операции дизъюнкции.
5. Функции – Булевой (логической) функцией называется такая функция, аргументами которой являются булевы переменные, и сама функция принимает значение из множества {0;1}.
Областью определения Булевой функции является совокупность 2m двоичных наборов ее аргументов. Набор аргументов можно рассматривать как m-компонентный двоичный вектор.
5.1 Аналитическая (в виде логического выражения) представляется следующим образом: 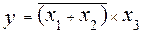 .
.
5.2 Табличная (в виде таблицы истинности) представляющей собой совокупность всех наборов переменных и соответствующих им значений функции.
Таблица истинности содержит К=2m строк, m столбцов (по количеству входов) и один столбец для записи значения функции.
Например: пусть требуется задать функцию трех переменных F (Х3,Х2,Х1) (рис. 2.1), ее реализует логическая схема, имеющая три входа и один выход ( m=3, К=8).

Рис.2.1. Таблица истинности и функциональное обозначение логической схемы (ЛС) с тремя входами и одним выходом
5.3 Числовая:
В этом случае функция задается в виде десятичных эквивалентов номеров наборов аргументов, при которых функция принимает единичное значение. Например, для рассмотренного выше примера функция F принимает единичные значения на наборах переменных со следующими номерами: 1, 2, 5, тогда числовой способ задания будет иметь вид: F(X1,X2,X3)=(1,2,5)X3,X2,X1.
5.4 Графическая:
Подобный подход носит ограниченный характер и, как правило, является наглядным для булевых функций от 2-х и 3-х переменных. Для примера представим графическую интерпретацию (см. рис. 2.2) булевой функции 3-х переменных, представленную в числовой форме: F(x)=V(1,2,3,6,7).
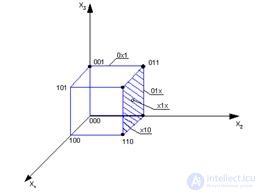
Рис. 2.2. Графическое представление функции трех переменных
5.5 Таблично-графическая или координатная:
При этом способе булевая функция задается с помощью карты состояния, которая известна как карта Карноили диаграмма Вейча.
Карта Карно содержит 2m клеток по числу наборов значений переменных. Каждая клетка определяется координатами строк и столбцов, соответствующими определенному набору переменных. Все входные переменные разбиваются на 2 группы так, что одна группа определяет координаты строк, а другая - координаты столбцов. В каждой клетке карты Карно проставляется соответствующее значение функции на заданном наборе. Пример задания функции трех переменных приведен на рис. 2.3. Числовое выражение этой функции выглядит так: F(X)=(2, 3, 6)X3,X2,X1; К=2m; m=3; K=8.
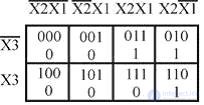
Рис. 2.3. Карта Карно для функции трех переменных
6. Законы(тождества) Булевой алгебры:
Ниже приведены основные, наиболее часто применяемые при синтезе комбинационных схем, законы.
Закон перестановки: 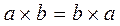 и
и 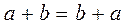 .
.
Ассоциативный закон:  и
и  .
.
Дистрибутивный закон: 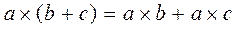 и
и 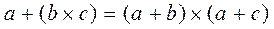 .
.
Закон двойного отрицания: 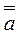 =
=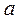 .
.
Тавтологии: 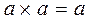 и
и 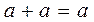 .
.
Закон нулевого элемента: 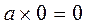 и
и 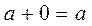 .
.
Закон единичного элемента:  и
и 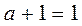 .
.
Закон дополнительного элемента: в Булевой алгебре дополнительным элементом к 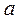 является
является 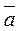 , поэтому:
, поэтому:  и
и 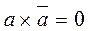 .
.
Закон двойственности (дуальности, де-Моргана): 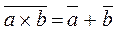 и
и 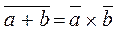 .
.
Как следствие из этого закона вытекает: 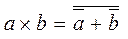 и
и  .
.
Закон поглощения: 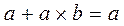 и
и 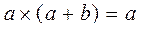 .
.
Закон сокращения: 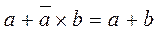 и
и 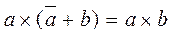 .
.
Как следствие из этого закона вытекает: 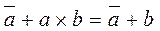 и
и  .
.
Закон склеивания: 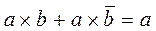 и
и 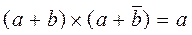 .
.
Даже самые сложные преобразования цифровой информации, в конечном счете, сводятся к простейшим операциям над логическими переменными 0 и 1. Такие операции реализуются логическими элементами в соответствии с формулами алгебры логики.
В реальных условиях логическим переменным 0 и 1 соответствуют, как правило, различным уровням напряжения: U0 и U1. Переход от логических переменных к электрическим параметрам ставит вопрос о логических соглашениях. Необходимо условиться, какой из двух уровней напряжения принять за U0 и какой за U1. Существуют соглашения положительной (позитивной) и отрицательной(негативной) логики. Принято считать, что в положительной логике U1> U0, а вотрицательной U1< U0. Необходимо понимать, что, в зависимости от принятого логического соглашения, один и тот же логический элемент выполняет различные логические операции. Переход от операции в положительной логике к операции в отрицательной производится инвертированием всех переменных.
В дальнейшем, если не будет специально оговорено, будем пользоваться соглашениями положительной логики.
Одни и те же преобразования логических переменных можно задать в различных формах (базисах): с помощью операций И, ИЛИ, НЕ (булевский базис), операцииИ-НЕ (базис Шеффера), операции ИЛИ-НЕ (базис Пирса), а также многими другими способами. Выбора базиса зависит от простоты реализации той или иной логической функции с помощью электрических схем данной схемотехнологии. Чаще всего встречаются базисы Шеффера и Пирса. В различных сериях стандартных ИС наряду с базовыми логическими элементами обычно имеется и ряд других, выполняющих другие логические операции.
Для правильного проектирования и эксплуатации цифровых устройств (ЦУ) необходимо знать систему параметров логических элементов (статических и динамических).
К важнейшим статическим параметрам относятся четыре значения напряжения и четыре значения тока:
ü параметры напряжений:
Ø входное напряжение лог. «1» ― Uвх.1,
Ø входное напряжение лог. «0» ― Uвх.0,
Ø выходное напряжение лог. «1» ― Uвых.1,
Ø входное напряжение лог. «0» ― Uвых.0.
Для нормальной работы элемента требуется, чтобы напряжение, соответствующее лог. «1», было достаточно высоким, а напряжение лог. «0» - достаточно низким. Эти требования задаются параметрами Uвх.1min и Uвх.0max. Входные напряжения данного элемента есть выходные напряжения предыдущего (источника сигналов). Уровни, гарантируемые на выходе элемента при соблюдении допустимых нагрузочных условий, задаются параметрами Uвых.1min и Uвых.0max. Как правило, выходные уровни несколько «лучше» входных, что обеспечивает определенную помехоустойчивость элемента. Для уровня U1 опасны отрицательные помехи, снижающие его, причем уровень допустимой статической помехи (т.е. помеха любой длительности) д.б. не выше U-пом= Uвых.1min - Uвх.1min. Для уровня U0 опасны положительные, уровень допустимой статической помехи которой, д.б. не выше U+пом= Uвых.0max - Uвх.0max.
ü параметры тока:
Ø входной ток лог. «1» ― Iвх.1,
Ø входной ток лог. «0» ― Iвх.0,
Ø выходной ток лог. «1» ― Iвых.1,
Ø выходной ток лог. «0» ― Iвых.0.
При высоком уровне выходного напряжения из элемента-источника ток вытекает, цепи нагрузки этот ток поглощают. При низком уровне выходного напряжения элемента-источника ток нагрузки втекает в этот элемент из входных цепей элемента-приемника. Зная токи Iвых.0max и Iвых.1max, характеризующие возможности элемента-источника сигнала и токи Iвх.0max и Iвх.1max, потребляемые элементами-приемниками, можно контролировать соблюдение нагрузочных ограничений, обязательное для всех элементов ЦУ.
Быстродействие относится к наиболее важным динамическим параметрам логических элементов (ЛЭ). Быстродействие определяется скоростями их перехода из одного состояния в другое. Быстродействие ЦУ определяется задержками сигналов, как в
 ЛЭ, так и в цепях их межсоединений.
ЛЭ, так и в цепях их межсоединений.
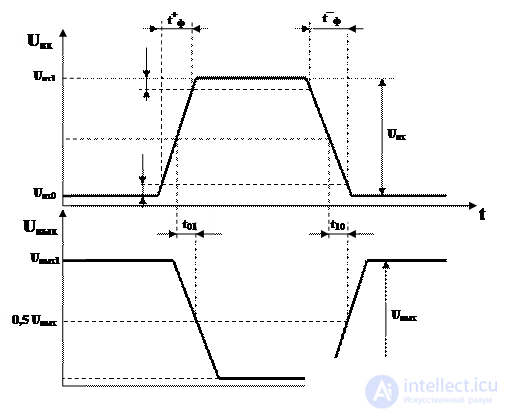
Рис. 2.4. Временные диаграммы процесса переключения ЛЭ
Временные диаграммы переключения инвертирующего ЛЭ (рис. 2.4) показывают длительности характерных этапов переходных процессов, отсчитываемые по, так называемым, измерительным уровням. Моментом изменения логического сигнала считают момент достижения одного из логических уровней. Часто за пороговый уровень принимают середину логического перепада сигнала, т.е. 0,5(U0+U1). Иногда пороговый уровень указывается более точно в паспортных данных элемента. На временных диаграммах показаны задержки распространения сигнала при изменении выходного напряжения элемента от U1 до U0 и обратно (t10+t01). Очень часто для упрощения расчетов пользуются усредненным значением задержки распространения сигнала tз=0,5(t10+t01).
При разработке цифрового устройства (ЦУ) требуется оценить его мощность потребления, чтобы сформулировать требования к источникам питания и конструкции теплоотвода. При этом суммируются мощности, рассеиваемые логическими и другими элементами схемы. Мощности, потребляемые ЛЭ, подразделяют на статические и динамические. Статическая мощность потребляется ЛЭ, который не переключается. При переключении потребляется дополнительная динамическая мощность, которая пропорциональна частоте переключения. Таким образом, полная мощность зависит от частоты переключения, что и следует учитывать при ее подсчете.
Цифровые элементы (логические, запоминающие, буферные) могут иметь выходы следующих типов: логические, с третьим состоянием, с открытым коллектором(стоком) и с открытым эмиттером (истоком). Наличие четырех типов выходов объясняется условиями работы элементов в логических цепях, в магистрально-модульных микропроцессорных системах и т.п.
Логический выход формирует два уровня выходного напряжения (U0 и U1). Выходное сопротивление логического выхода стремятся сделать малым, способным развивать большие токи для перезаряда емкостных нагрузок и, следовательно, получения высокого быстродействия элемента. Такой тип выхода имеют большинство ЛЭ, используемых в комбинационных цепях.
Схемы логических выходов элементов ТТЛ(Ш) и КМОП логики подобны двухтактным каскадам – в них оба фронта выходного напряжения формируются с участием активных транзисторов, работающих противофазно, что обеспечивает малые выходные сопротивления при любом напряжении переключения выхода (см. рис. 2.5).
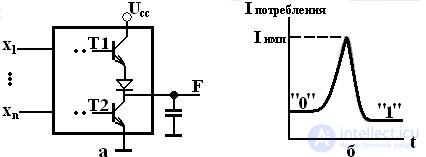
Рис. 2.5. Схема выходной цепи элемента ТТЛ (а) и график изменения потребленного им тока в процессе переключения (б)
Особенность таких выходов состоит в том, что их нельзя соединить параллельно. Во-первых, это создает логическую неопределенность, т.к. в точке соединения выхода, формирующего лог. «1», и выхода, формирующего лог. «0», возникло бы их «противоборство». Во-вторых, вследствие малых величин выходных сопротивлений уравнительный ток в этом случае может достигать достаточно большой величины, что может привести к выходу из строя электрических элементов выходной цепи и, соответственно, элемента в целом.
Вторая особенность логического выхода двухтактного типа связана с протеканием через оба транзистора коротких импульсов тока при переключениях из одного состояния в другое. Эти токи протекают от источника питания на общую точку («землю»). В статических состояниях таких токов быть не может, т.к. транзисторы Т1 и Т2 работают в противофазе, т.е. один из них находится в запертом состоянии. Однако, в переходном процессе из-за некоторой несинхронности переключения транзисторов возникает кратковременная ситуация, при которой оба транзистора открыты, что и порождает короткий импульс сквозного тока, протекающего через оба транзистора, значительной величины (рис. 2.5, б).
Элементы с тремя состояниями выхода (типа ТС) кроме логического состояния «0» и «1» имеют третье состояние – «отключено» или состояние высокого импеданса (“impedance” - сопротивление), в котором ток выходной цепи пренебрежительно мал. В третье состояние элемент переводится специальным управляющим сигналом, который обеспечивает запертое состояние обоих транзисторов (Т1 и Т2 на рис. 2.5, а) Сигнал управления элементом типа ТС обычно обозначают ОЕ (Output Enable). При наличии разрешения (ОЕ=1) элемент работает в режиме логического выхода, а при его отсутствии (ОЕ=0) переходит в состояние «отключено». В ЦУ широко используются буферные элементы типа ТС для управляемой передачи сигналов по одним и тем же линиям. Буферы могут быть не инвертирующие и инвертирующие, а сигналы ОЕ H – активные (лог. «1» - высокий уровень) и L – активные (лог. «0» - низкий уровень).
Выходы типа ТС отмечаются в обозначениях элементов значком  . Их можно соединять параллельно при условии, что в любой момент времени активным может быть только один из параллельно соединенных выходов. В этом случае отключенные выходы не мешают активному формировать сигналы в точке соединения выходов, т.к. их выходное сопротивление достаточно велико.
. Их можно соединять параллельно при условии, что в любой момент времени активным может быть только один из параллельно соединенных выходов. В этом случае отключенные выходы не мешают активному формировать сигналы в точке соединения выходов, т.к. их выходное сопротивление достаточно велико.
Элементы с третьим состоянием сохраняют такие достоинства элементов с логическим выходом, как быстродействие и высокая нагрузочная способность. Поэтому они являются основными в указанных применениях. В то же время они требуют обязательного соблюдения условия отключения всех выходов, соединенных параллельно, кроме одного, т.е. условия ОЕ1+ ОЕ2+…+ ОЕn≤1 при объединении n выходов. Нарушение этого условия может привести даже к выходу из строя элементов.
Элементы с открытым коллектором имеют выходную цепь, заканчивающуюся одиночным транзистором, коллектор которого не соединен с какими-либо цепями внутри микросхемы (рис. 2.6,а).
Транзистор управляется от предыдущей части схемы элемента так, что может находиться в насыщенном или запертом состоянии. Насыщенное состояние транзистора соответствует лог. «0», а запертое – лог. «1». Насыщение транзистора обеспечивает на выходе малый уровень напряжения (напряжение насыщения «коллектор – эмиттер»). Запирание же транзистора какого-либо напряжения на выходе не задает, выход при этом имеет фактически неизвестный «плавающий» потенциал, т.к. не подключен к каким-либо цепям схемы элемента. Поэтому для формирования высокого уровня напряжения при запирании транзистора на выходе элементов с открытым коллектором (типа ОК) требуется подключать внешние резисторы (или другие нагрузки), соединенные с источником питания.

Рис. 2.6. Схема выходной цепи элемента с открытым коллектором (а) и реализация монтажной логики (б)
Несколько выходов типа ОК можно соединить параллельно, подключая их к общей для всех выходов цепочке Ucc-R (рис. 2.6,б). При этом можно получить режим поочередной работы элементов на общую линию, как для элементов типа ТС, если активным будет лишь один элемент, а выходы всех остальных окажутся запертыми. Если же разрешить активную работу всем элементам, подключенным к одной линии, то можно получить дополнительную логическую операцию, так называемую операциюмонтажной логики.
При реализации монтажной логики высокое напряжение на общем выходе возникает только в том случае, когда заперты выходные транзисторы всех элементов, электрически соединенных по выходу, т.к. насыщение хотя бы одного из них снижает выходное напряжение до уровня U0 = Uкэн. Т.е. для получения лог. «1» на выходе требуется состояние лог. «1» на всех выходах. Таким образом выполняется монтажная операция И. Поскольку каждый элемент выполняет операцию Шеффера (И-НЕ) над своими входными переменными, общий результат будет следующим:
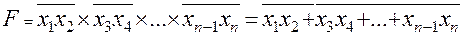
В обозначении элементов с ОК после символа функции ставится ромб с черточкой снизу. На рис. 2.6,б изображены элементы монтажной логики И-НЕ.
При использовании элементов с ОК в магистрально-модульных структурах требуется разрешать или запрещать работу того или иного элемента. Для элементов типа ТС это делалось с помощью специального сигнала ОЕ. Для элементов типа ОК в качестве входа ОЕ может быть использован один из обычных входов элемента. Если речь идет об элементе И-НЕ, то, подавая лог. «0» на любой из входов, можно запретить работу элемента, поставив его выход в разомкнутое состояние независимо от состояния других входов. Лог. «1» на этом входе разрешит работу элемента.
Положительными свойствами элементов с ОК при работе в магистрально-модульных системах является их защищенность от повреждений из-за ошибок управления, приводящих к одновременному подключению к магистрали нескольких элементов, а также возможность реализации дополнительных операций монтажной логики. Недостатком таких элементов является большая задержка переключения из лог. «0» в лог. «1». При этом переключении происходит заряд выходной емкости сравнительно малым током, протекающим через резистор R, сопротивление которого нельзя сделать слишком малым, т.к. это приведет к большим токам выходной цепи в статике при насыщенном состоянии выходного транзистора. Значение сопротивления резистора R проектировщик при работе с элементами типа ОК выбирает с учетом требуемого быстродействия схемы и потребляемой ею мощности. При этом, выбор значения сопротивления, близкого к минимально допустимому позволит достичь максимального быстродействия, а к максимально допустимому – к минимальной мощности потребления.
Выход с открытым эмиттером характерен для элементов типа ЭСЛ
( эмиттерно-связанная логика). Для работы на магистраль такие элементы не используются. Возможность соединять друг с другом выходы с открытым эмиттером при объединении эмиттерных резисторов в один общий резистор приводит к схеме, используемой при построении логических схем для получения дополнительной операции монтажной логики (рис. 2.7).

Рис. 2.7. Схема выходного цепи элемента с открытым эмиттером
Элементы ЭСЛ имеют противофазные выходы, на одном из которых реализуется функция ИЛИ, на другом – ИЛИ-НЕ. Соединяя прямые выходы нескольких элементов, получают расширение по ИЛИ (входные элементы нескольких элементов образуют единую дизъюнкцию). Соединяя инверсные выходы, получают операцию И-ИЛИ относительно инверсных входных переменных т.к. при этом:
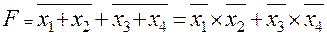 .
.
Соединяя прямой выход одного элемента с инверсным выходом второго элемента, можно получить функцию вида:
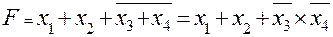 .
.
При построении КС устройств вычислительной техники используются различные логические элементы, которые должны согласоваться по входным и выходным сигналам, напряжению питания и т.д. Для этой цели логические элементы объединяют в серии.
Серией (системой, комплексом) логических элементов ЭВМ называется предназначенный для построения цифровых устройств функционально полный набор логических элементов, объединяемый общими электрическими, конструктивными и технологическими параметрами, использующий одинаковый способ представления информации, одинаковый тип межэлементных связей. Система элементов чаще всего избыточна по своему функциональному составу, что позволяет строить схемы более экономичные по количеству использованных элементов.
В состав серии входят элементы для выполнения логических операций, запоминающие элементы, элементы, реализующие функции узлов ЭВМ, а также специальные элементы для усиления, восстановления и формирования сигналов стандартной формы.
Конструктивно логические элементы представляют собой микроминиатюризированые интегральные электронные схемы (микросхемы), сформированные в кристалле кремния с помощью специальных технологических процессов.
В большинстве современных серий элементов имеются микросхемы малой степени интеграции (ИС до 100 элементов на кристалле), средней степени (СИС – до 1000 элементов на кристалле), большой степени интеграции (БИС – до 10000 элементов на кристалле) и сверхбольшой степени интеграции (СБИС – более 10000 элементов на кристалле). Логические элементы в виде ИС реализуют совокупность простых логических операций: И, ИЛИ, И-ИЛИ, И-НЕ, ИЛИ-НЕ и т.д. Логические элементы на СИС и БИС реализуют узлы ЭВМ, на СБИС – микроЭВМ.
Основными параметрами серии логических элементов являются:
Ø питающие напряжения и сигналы для представления лог. «0» и лог. «1»;
Ø коэффициенты объединения по входу;
Ø нагрузочная способность (коэффициент разветвления по выходу);
Ø помехоустойчивость;
Ø рассеиваемая мощность;
Ø быстродействие.
Серия элементов характеризуется количеством используемых питающих напряжений и их номинальными значениями. Обычно лог. «0» соответствует низкий уровень напряжения, а лог. «1» – высокий. Для наиболее часто используемых серий напряжение питания составляет +5В, уровень логической единицы 2,4-5В, уровень логического 0 – 0-0,4В.
Коэффициент объединения по входу (Коб) определяет максимально возможное число входов логического элемента, иными словами, функцию скольких переменных может реализовать этот элемент. Обычно Коб принимает значение от 2 до 4, реже Коб= 8. Увеличение числа входов связано с усложнением схемы элементов и приводит к ухудшению других параметров – помехоустойчивости, быстродействия и т.д.
Коэффициент разветвления по выходу (Краз) показывает на какое количество логических входов может быть одновременно нагружен выход данного логического элемента. Обычно Краз для наиболее часто используемых серий равен 10. Иногда вместо Краз задается предельно допустимое значение выходного тока логического элемента в состоянии «0» или «1».
Помехоустойчивость – это способность элемента правильно функционировать при наличии помех. Она определяется максимально допустимым напряжением помехи, при котором не происходит сбоя в его работе. Обычно это напряжение порядка 0,6-0,9 В.
Быстродействие логических элементов является одним из важнейших параметров и характеризуется временем задержки распространения сигнала. Этот параметр существенно зависит от технологии изготовления микросхем и лежит в диапазоне от единиц до сотен наносекунд.
Сравнительные характеристики наиболее употребляемых серий логических элементов приведены в табл.2.1., где в первой колонке приведены зарубежные обозначения серий, во второй – отечественные.
| Отечест венный аналог | Напря жение питания Vcc+_10%, B | Совместимость | Входной ток~ IIL/IIH, мкА/мкА | Нагрузка~ IOL/IOH, мА/мА | Ток потреб- ления~ ICC, мкА | Быс тро дейст вие, нс | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| по входам VIL/VIH | по выходам VOL/VOH | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| BICMOS | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ABT LVT(16) | - - | 5 3,3 | TTL TTL,CMOS | TTL TTL,CMOS | -5/5 -5/1 | 64/-32 64/-32 | 30 mA 9,0 mA | 3,6 4,1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| CMOS | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Биполярные | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1. Назовите элементы, из которых состоит Булева алгебра.
2. Дайте определение простейшим логическим функциям Булевой алгебры.
3. Перечислите формы задания Булевых функций.
4. Дайте определение и приведите пример табличной формы задания Булевой функции.
5. В чем отличие числовой и аналитической форм задания Булевых функций.
6. Дайте пример координатной формы задания Булевой функции.
7. Запишите основные законы Булевой алгебры.
8. Чем отличается положительная логика от отрицательной.
9. Чем отличаются различные типы выходных каскадов логических элементов.
10. Что такое операции монтажной логики.
11. Что называется серией логических элементов.
12. Перечислите основные параметры серии логических элементов.
13. Дайте определение коэффициента разветвления по выходу.
Надеюсь, эта статья про логические построения элементов, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое логические построения элементов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Компьютерная схемотехника и архитектура компьютеров
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Компьютерная схемотехника и архитектура компьютеров
Термины: Компьютерная схемотехника и архитектура компьютеров