Тема 3. Схемотехника комбинационных узлов

Привет, сегодня поговорим про схемотехника комбинационных узлов, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое схемотехника комбинационных узлов , настоятельно рекомендую прочитать все из категории Компьютерная схемотехника и архитектура компьютеров.

Лекция 3 3.1 Общие сведения

Под комбинационными понимают узлы, не содержащие элементов памяти. В таких узлах всякое изменение состояния входных сигналов вызывает соответствующее изменение выходных сигналов с задержкой, определяемой длительностью переходных процессов в данном узле. В общем случае комбинационный узел (КУ) содержит несколько входов и несколько выходов. Поведение комбинационного узла описывается функциями алгебры логики (булевыми или логическими функциями). При этом для каждого выхода можно определить соответствующую булеву функцию, которая полностью определяет поведение комбинационного узла по данному выходу без учета задержки распространения сигнала, то есть для идеального узла.

Время задержки сигнала по каждому выходу может быть разным. Время задержки зависит и от того, какой входной сигнал изменением своего состояния привел к соответствующему изменению данного выходного сигнала.

Поведение комбинационного узла может быть задано таблицей истинности, в которой каждой комбинации значений входных сигналов ставится в соответствие значение каждой выходной переменной. Входные переменные будем обозначать буквой X с соответствующим индексом, а выходные - буквой Y с соответствующим индексом. По известной таблице истинности можно для каждого выхода составить соответствующую булеву функцию. Количество комбинационных узлов, которые можно синтезировать, огромно даже при достаточно небольшом числе входных переменных. Но практике в большинстве случаев не требуется собственно разработки нового комбинационного узла, а достаточно ограничиться применением известных схемных решений, реализованных в виде микросхем. Достаточно лишь разумно использовать стандартные микросхемы.

Выделим следующие комбинационные узлы, которые реализованы в виде

микросхем: дешифраторы и шифраторы, мультиплексоры и демультиплексо-ры, шинные формирователи, компараторы цифровых сигналов, сумматоры, арифметико-логические устройства и умножители.

В комбинационных узлах можно выделить информационные, адресные иуправляющие входы. Управляющие входы помечают меткой E (Enable – разрешение). Информационные и адресные входы помечаются цифровыми метками, которые могут обозначать номер по порядку или вес двоичной переменной, подаваемой на данный вход. Вес указывают или степенью двойки, в которую следует возвести двойку, чтобы получить реальный вес разряда, или действительным значением веса разряда. Для входов и выходов узла можно определить понятие активного и пассивного сигнала. Под активным понимают тот уровень сигнала, который вызывает определенные действия или представляет интерес. Если активным является уровень единицы, то соответствующий вывод является прямым и изображается так, как показан прямой вход разрешения работы на рисунке 3.1,а. Если активным является нулевой уровень, то соответствующий вывод помечается инвертирующим кружком, как показано на рисунке 3.1,б. Прямой Инверсный вход вход

а) б) Рис. 3.1.-Примеры изображения входов разрешения

3.2. Шифраторы, дешифраторы и преобразователи кодов: назначения, виды, функционирование, принципы построения

Шифраторы (кодеры) – устройства, предназначенные для преобразования алфавитно-цифровой информации, поданной унитарным n-разрядным кодом в эквивалентный двоичный m-разрядный код. Особенностью унитарного кода является активное состояние только одной переменной X_i входного набора{X_n-1…X₁ X₀}, порядковый номер i которой подлежит кодированию. Т.е. шифратор n-m – это преобразователь унитарного кода «1 из n» в двоичный (параллельный) код, у которых число выходов mоднозначно связано с числом входов n как 2^m. При n =2^m используется полный набор выходных двоичных комбинаций Y_i. Такой шифратор называется полным. Например, шифратор 8-3 полный, т.к. он реализует полный набор возможных комбинаций переменных X_i(n=8) в полный выходной набор Y_i(m=3)как 2³=8.

В неполном шифраторе число входов n не соответствует числу всех возможных выходных комбинаций2^m (n <2^m), что соответственно создает некоторое число неиспользованных выходных наборов. Примером неполного шифратора является шифратор 10-4, используемый для кодирования десятичных чисел в двоичный код (8-4-2-1).

При синтезе полного (неполного) шифратора достаточно реализовать в заданном базисе систему логических функций Y_i, которые создают на его m выходах слово {Y_m-1 …Y₁ Y₀}. Например, полный шифратор 8-3 описывается таблицей истинности (табл. 3.1) и системой логических функций:

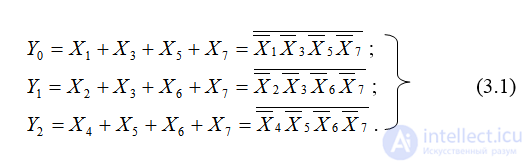
Таблица 3.1 Таблица истинности полного шифратора 8-3

Из системы логических функций следует, что шифратор 8-3 реализуется в базисе ЛЭ 4ИЛИ (рис. 3.1). Y₀ - выход младшего разряда весом 2⁰, Y₁ - 2¹ и Y₂ – выход старшего разряда весом 2².

Неполный шифратор реализуется аналогично полному, однако, отсутствуют те наборы переменных, которые не используются при кодировании. В шифраторе 10-4 неиспользованных выходных наборов будет 2⁴-10=6 – Y_i:{1010}, {1011}, {1100}, {1101}, {1110}, {1111}.

Приведенный на рис. 3.1 шифратор – линейный, все ЛЭ присоединяются к одной общей шине (линии). Для реализации линейного шифратора необходимо иметь многовходовые ЛЭ. Переменная X₀ не задействована (табл. 3.1). Это означает, что при любом сигнале на входе X₀ на выходе шифратора не будет никаких изменений.

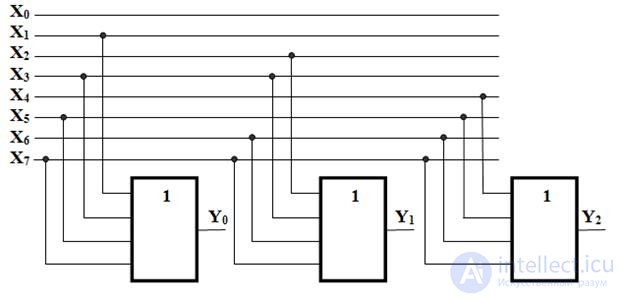
Рис. 3.1. Схема функциональная полного шифратора

Меньшим быстродействием кодирования обладают пирамидальные шифраторы, построенные по принципу использования однотипных, например, двухвходовых ЛЭ 2И-НЕ. Структурная схема таких шифраторов похожа на пирамиду. Число ЛЭ не зависит от разрядности m кодированного слова.

В линейных и пирамидальных шифраторах реализуется обязательное соответствие выходного m-разрядного кода одному активному входу. Чтобы шифратор реагировал только на один из нескольких активных входов, его схему строят по приоритетному принципу.

В приоритетном шифраторе выходной код всегда соответствует тому активному входу, который имеет наибольший номер набора. Например, на выходе приоритетного шифратора при активных входах Х₁, Х₂, Х₄ появится код {100}, что соответствует переменному Х₄ (активные входы Х₁ и Х₂ игнорируются).

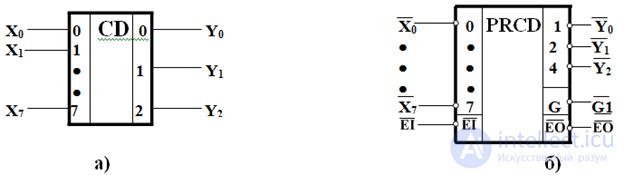
Рис.3.2. Условное графическое изображение полного (а) и приоритетного (б) шифраторов

В промышленных сериях элементов имеются шифраторы приоритета для восьмиразрядных и десятиразрядных слов. Функционирование восьмиразрядного приоритетного шифратора описывается таблицей истинности (табл. 3.2).

Таблица 3.2 Таблица истинности восьмиразрядного приоритетного шифратора

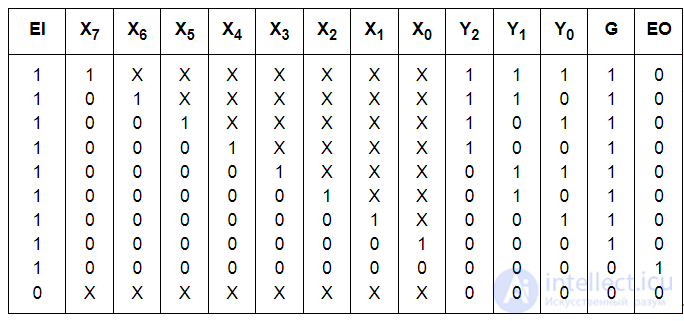
Таблица 3.2 характеризует работу приоритетного шифратора при всех возможных комбинациях сигналов. На рисунке 3.2,б показано его условное графическое изображение, сигнал EI – разрешение работы шифратора; ЕО – сигнал, вырабатываемый на выходе шифратора при отсутствии запросов на его входах, служит для разрешения работы следующего (младшего) шифратора при наращивании размерности шифраторов; G – сигнал, отмечающий наличие запросов на входе; Х₀…Х₇ – запросы на входах; Y₂…Y₀– значения разрядов выходного двоичного кода, формируемые по номеру старшего активного запроса. Все перечисленные сигналы формируются при условии ЕI=1 (работа разрешена). При ЕI=0 независимо от состояния входов запросов все выходные сигналы становятся нулевыми.

Из таблицы 3.2 можно записать выражения для Y₂, Y₁, Y₀, EO и G:

Линейные шифраторы используются для передачи информации в интерфейсных устройствах, при сжатии информации, передаваемой с помощью малого числа линий связи.

Приоритетные шифраторы могут использоваться для цифро-аналогового и аналого-цифрового преобразования, а также для реализации приоритетного кодирования и прерывания в микропроцессорной схемотехнике.

Дешифраторы (декодеры) – устройства для распознавания числа, поданного позиционнымn-разрядным кодом. Дешифраторы относятся к преобразователям кодов. Дешифратор n-mвыполняет функцию преобразования двоичного кода в унитарный код «1 из m», т.е. выполняет функцию, обратную шифратору. Для полного дешифратора m=2ⁿ, где m – порядковый номер выхода Y_i дешифратора. В неполном дешифраторе число выходов m не соответствует 2ⁿ (m<2ⁿ).

В условном графическом обозначении (рис. 3.3,б) входы дешифратора обозначают их двоичными весами. Помимо информационных входов дешифратор обычно имеет один или более входов разрешения работы (EN). При наличии разрешения по этому входу, дешифратор работает описанным выше образом, при его отсутствии – все выходы дешифратора пассивны. Если входов разрешения несколько, то сигнал разрешения работы образуется как конъюнкция сигналов отдельных входов разрешения. Часто дешифратор имеет инверсные выходы. В этом случае только один выход имеет нулевое значение, а все остальные – единичное, а при запрещении работы на всех выходах будет присутствовать логическая единица. Функционирование полного дешифратора (n – m)описывается системой (3.3):

Как следует из системы конъюнкции (3.3), каждому из m выходов полного дешифратора соответствует одна из 2ⁿ кодовых комбинаций (минтерм или макстерм) n - разрядного входного слова {X_n-1…X₁ X₀}.

В неполном дешифраторе есть некоторое число неиспользованных входных наборов.

Схемы полного или неполного дешифраторов так же, как и шифраторов, можно собрать по линейной или пирамидальной структуре.

Число выходов полного четырехразрядного дешифратора равно 16 (2⁴=16). Полный дешифратор 4-16 описывается системой булевых функций (3.4):

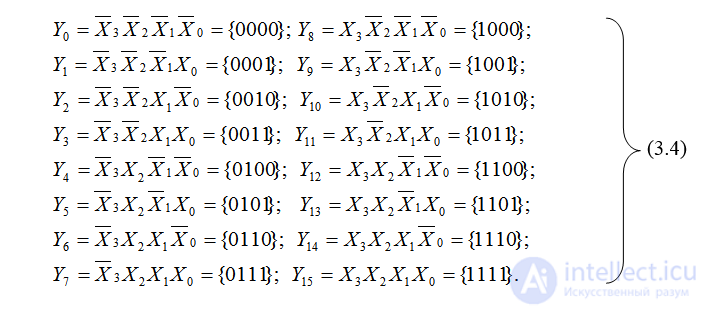
На рисунке 3.3,а представлена схема функциональная полного дешифратора 4-16, функционирующего в соответствии с таблицей 3.3.

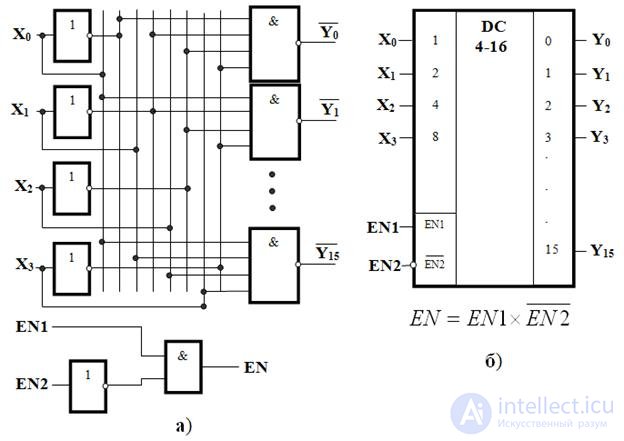
Рис. 3.3. Схема функциональная полного дешифратора 4-16 (а), условное графическое обозначение двоичного дешифратора 4-16 (б)

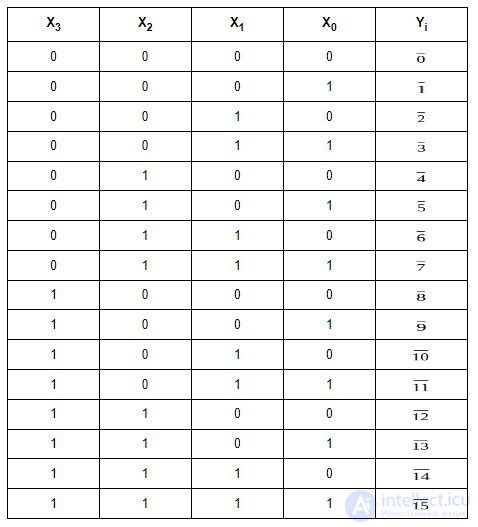
Таблица 3.3 Таблица истинности полного дешифратора 4-16

В случаях, когда необходимо создать дешифратор на большее число выходов на основе дешифраторов с меньшим числом выходов, используют принцип наращивания. Он заключается в том, что данные входы дешифраторов разбивают произвольным образом на группы, каждая из которых реализует свою группу логических функций.

Рис. 3.4. Схема функциональная двухкаскадного дешифратора

На рисунке 3.4 приведено двухкаскадное соединение двух дешифраторов. Первый каскад работает при активных входах Х₀, Х₁, Х₂иХ₃ при условии, что Х₄=0. Как только на входах дешифратора появится код 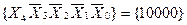, первый каскад закроется, т.к., откроется второй каскад, получающий через инвертор разрешающий уровень .

Дешифраторы используются в устройствах визуальной индикации, совместно со схемами ИЛИ их можно использовать для воспроизведения произвольных логических функций.

Линейные дешифраторы обеспечивают преобразование кода с минимальной задержкой и используются в наиболее быстродействующих цифровых схемах. Однако с ростом разрядности входного кода быстро возрастает нагрузка каждого из входов и количество корпусов интегральных микросхем (ИМС) для реализации дешифратора. Линейная структура обычно используется для построения дешифраторов с количеством входов ≤4.

Если число входов >4, то с целью уменьшения количества корпусов ИМС, дешифраторы выполняются по многоступенчатой схеме. Такие дешифраторы называютсяпирамидальными. Первой ступенью пирамидального дешифратора является простейший линейный дешифратор. Каждая последующая ступень, управляемая дополнительной входной переменной, позволяет удвоить количество выходов, т.е. k -ступенчатый полный пирамидальный дешифратор имеет число выходов N=2^k+1, причем k=m-1 (при m=2 линейный и пирамидальный дешифраторы совпадают).

Преобразователи кодов применяют для преобразования двоичных кодов в двоичный дополнительный, двоично-десятичный, коды знаков русского или латинского алфавита, коды чисел любой системы счисления и наоборот.

Принцип построения преобразователей кодов рассмотрим на примере преобразования кода 8421 в код 2421. Обозначим переменные, соответствующие отдельным разрядам кода 8421, – Х₄Х₃Х₂Х₁, а кода 2421 – Y₄Y₃Y₂Y₁. В таблице истинности (табл. 3.4) приведено соответствие комбинаций обоих кодов.

Таблица 3.4 Таблица истинности преобразователя кода 8421 в код 2421

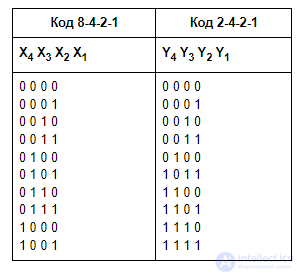
Каждая из переменных Y₄,Y₃,Y₂,Y₁ может рассматриваться функцией аргументов Х₄, Х₃, Х₂, Х₁ и, следовательно, представлена через эти аргументы соответствующим логическим выражением. Об этом говорит сайт https://intellect.icu . Для получения указанных логических выражений, представим переменные Y₄,Y₃,Y₂,Y₁ таблицами истинности в форме карты Карно (рис.3.5)

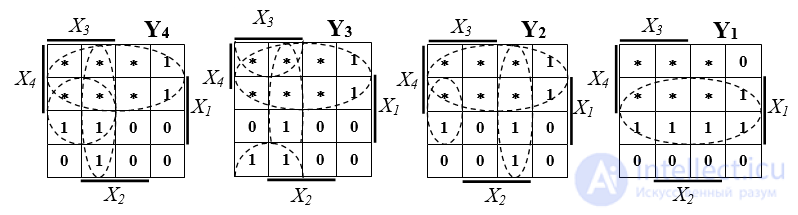
Рис. 3.5. Карты Карно для преобразователя кода 8-4-2-1 в код 2-4-2-1

По картам Карно получаем минимальную форму логических выражений в базисе И, ИЛИ, НЕ (3.5) и, выполнив преобразования 3.5, воспользовавшись правилом де Моргана, получаем эти же выражения в базисе И-НЕ (3.6).

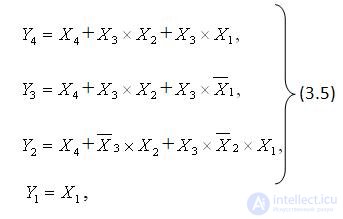
На рисунке 3.6 приведена логическая структура преобразователя кодов, построенная на элементах И-НЕ с использованием полученных логических выражений.

Рис. 3.6. Логическая структура преобразователя кода 8-4-2-1 в код 2-4-2-1 в базисе элементов И-НЕ

3.3. Синтез КС на основе дешифраторов

Дешифраторы со схемами ИЛИ можно использовать для воспроизведения произвольных логических функций. Действительно, на выходах дешифратора вырабатываются все конъюнктивные термы, которые только можно составить из данного набора аргументов. Логическая функция в совершенной дизьюнктивной нормальной форме (СДНФ) есть дизъюнкция некоторого числа таких термов. Собирая термы по схеме ИЛИ, можно получить любую функцию данного числа аргументов.

На рис. 3.7 в качестве примера показана схема выработки двух функций и 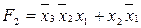. Такое решение может быть целесообразным при необходимости выработки нескольких функций одних и тех же аргументов. В этом случае для выработки дополнительной функции добавляется только один дизъюнктор. Заметим, что для проверки правильности схемы рис. 3.7 удобно перевести функции F₁ и F₂ в СДНФ.

Рис. 3.7 Схема выработки функций F₁ и F₂ с использованием дешифратора и схем ИЛИ

3.4. Мультиплексоры и демультиплексоры

Мультиплексор(коммутатор) – универсальное логическое устройство, на основе которого создают различные комбинационные и последовательные схемы, имеют один выход (Y₁) и более одного входа и осуществляющее коммутацию под действием управляющих сигналов (Х_k-1, Х_k-2, …, Х₁, Х₀) одного из информационных входных сигналов (D₀, D_1, …, D₂^k_-1) - на выход. Обычно 2^k=n, где k и n – число управляющих и информационных входов соответственно. Код, поступающий на управляющие входы, определяет один из информационных входов, значение переменной которого передается на выход Y₁.

C помощью мультиплексоров осуществляется разделение во времени информации, поступающей по разным каналам. Часто используются для преобразования параллельного кода в последовательный, в делителях частоты, триггерных и сдвигающих устройствах и пр.

Набор сигналов, поступающих на управляющие входы, задает двоичное число вида:

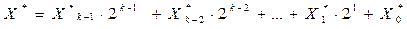, (3.7)

где Х_i^* =(0,1)- значение сигнала на входе Х_і. Выходной сигнал мультиплексора повторяет сигнал информационного входа D с номером Х^*.

Функция, реализуемая мультиплексором, может быть представлена в виде

++…+

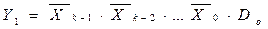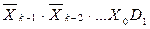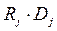+ = +++…+, (3.8)

где R_j –конъюнкция, равная 1 на наборе значений переменных Х_k-1,

Х_k-2,…,Х₀ c номером j (т.е. на наборе, представляющем в двоичном виде число j).

Таблица истинности, описывающая работу мультиплексора, имеющего n=8информационных и k=3 управляющих входов имеет вид, представленный в табл. 3.5. Часто мультиплексоры строятся с использованием элемента типа И-ИЛИ для коммутации сигналов и дешифратора для управления коммутацией. На рис. 3.8 представлена схема функциональная мультиплексора с двумя управляющими входами Х₀, Х₁ и его условное графическое обозначение.

Таблица 3.5 Таблица истинности мультиплексора, имеющего n=8 информационных и k=3 управляющих входов

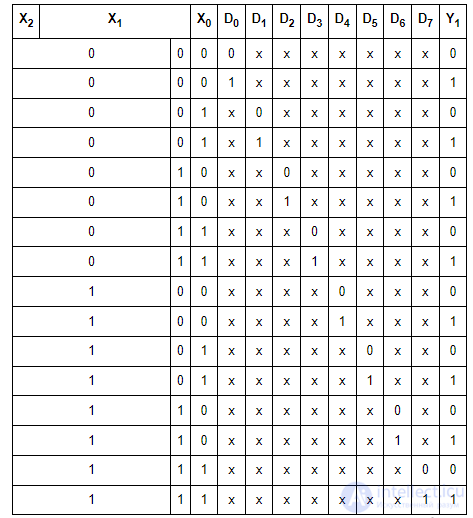
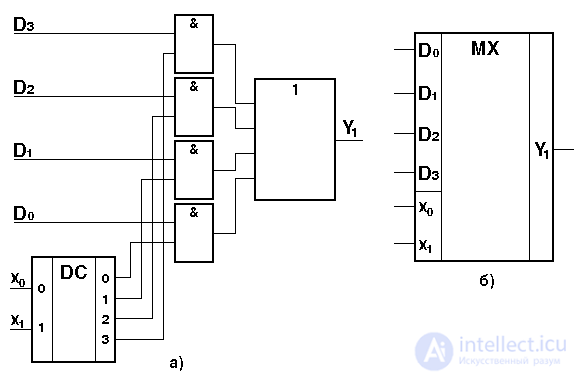
Рис. 3.8. Схема функциональная четырехканального мультиплексора с двумя управляющими входами (а) и его условное графическое обозначение (б)

Если необходимо расширить число входов, то используется каскадное включение мультиплексоров. На рисунке 3.9 приведена схема мультиплексора с четырьмя входами, построенного на основе двухвходовых мультиплексоров.

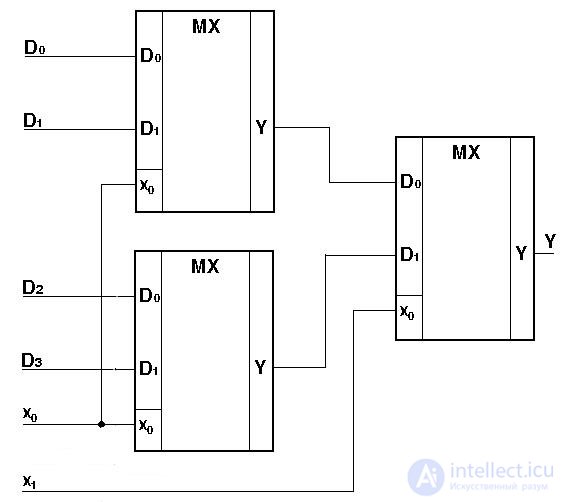
Рис. 3.9. Схема каскадного включения мультиплексоров

Демультиплексор – комбинационная схема, выполняющая функцию, обратную функции мультиплексора, т.е. это комбинационная схема, имеющая один информационный вход (D₁), n информационных выходов (Y₀, Y₁, Y_n-1), и k управляющих входов (X_k-1, X_k-2, … X₁, X₀). Обычно, также как и у мультиплексоров, 2^k=n. В зависимости от кода k на управляющих входах сигнал с единственного информационного входа выдается на один из n выходов.

Демультиплексоры часто используются для преобразования последовательного кода в параллельный.

Комбинационная схема демультиплексора реализует функцию (3.9):

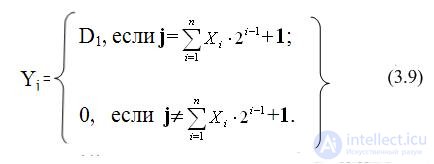
Работа демультиплексора описывается логическими уравнениями (3.10):

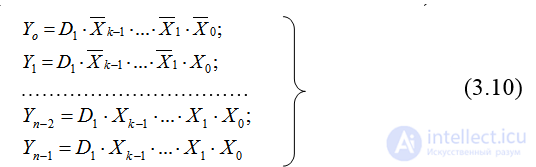
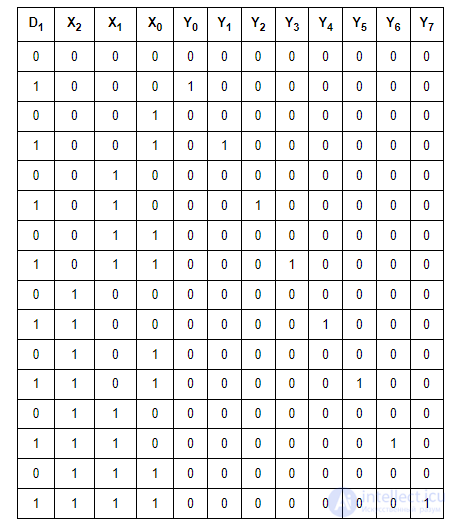
Таблица истинности, описывающая работу демультиплексора при n=8, k=3, представлена таблицей 3.6.

Таблица 3.6 Таблица истинности демультиплексора при n=8, k=3

В качестве демультиплексоров могут использоваться дешифраторы – демультикомплексоры.

На рисунке 3.10 представлена схема функциональная демультиплексора с четырьмя информационными выходами и двумя управляющими входами и его условное графическое изображение.

Рис. 3.10. Схема функциональная демультиплексора с прямыми управляющими входами (а) и его условное графическое изображение (б)

Для наращивания числа выходов демультиплексора используют каскадное включение демультиплексоров. На рисунке 3.11 приведена схема демультиплексора с шестнадцатью выходами на основе демультиплексоров с четырьмя выходами.

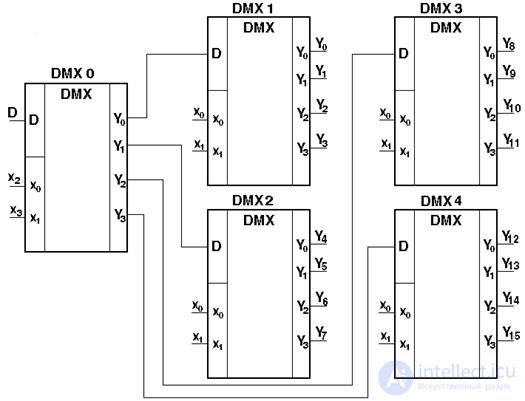
Рис. 3.11. Схема каскадного включения демультиплексоров

Функции демультиплексоров сходны с функциями дешифраторов. Дешифратор может рассматриваться как демультиплексор, у которого информационный вход поддерживает напряжение выходов в активном состоянии, а адресные входы выполняют роль входов дешифратора.

3.5. Шинные формирователи

Мультиплексоры предназначены для объединения нескольких выходов в тех случаях,

продолжение следует...

Продолжение:

Часть 1 Тема 3. Схемотехника комбинационных узлов
Часть 2 3.6 Синтез КС на основе мультиплексоров - Тема 3. Схемотехника
Часть 3 3.11.2 Основные факторы, которые должны быть учтены при построении принципиальных