Лекция
Привет, сегодня поговорим про схемотехника цифровых узлов, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое схемотехника цифровых узлов, цифровой автомат , настоятельно рекомендую прочитать все из категории Компьютерная схемотехника и архитектура компьютеров.
Как было указано в предыдущем разделе, большинство современных цифровых устройств являются последовательностными или цифровыми автоматами с памятью, состоящими из комбинационной схемы и элементов памяти – запоминающих элементов (ЗЭ) (рис.4.1). Там были рассмотрены
простейшие цифровые элементы, к которым относятся триггера, регистры, счетчики и распределители тактов. Простейшие цифровые устройства могут быть легко синтезированы при помощи рассмотренных логических и цифровых элементов. Более сложные цифровые устройства, называемые цифровыми узлами, удобнее рассматривать и проектировать с более общих позиций, используя теорию цифровых автоматов.
Под цифровым автоматом (ЦА) понимают устройство, предназначенное для преобразования дискретной информации. С общей точки зрения, процесс получения информации есть ни что иное, как процесс снятия неопределенности в результате того, что из некоторой совокупности возможных в данной конкретной ситуации явлений выделяется явление, фактически имевшее место.
В состав цифровых автоматов обязательно входят запоминающие элементы (элементы памяти). Выходные сигналы в таких автоматах формируются в зависимости от входных сигналов и состояний, в которых находятся элементы памяти. Наличие элементов памяти придает ЦА свойство иметь некоторое внутреннее состояние А, определяемое совокупностью состояний всех элементов памяти. В зависимости от внутреннего состояния ЦА различно реагируют на один и тот же набор входных сигналов. Воспринимая входные сигналы Z при определенном состоянии, ЦА в соответствии с заложенной в него программой переходит в новое состояние и вырабатываетвыходные сигналы W. Переходы ЦА из одного состояния в другое начинаются с некоторого исходного состояния, задание которого также является частью задания автомата. В конечном счете, текущее состояние и выходы автомата зависят от начального состояния и всех наборов входных сигналов, поступивших на автомат в предшествующие моменты времени. Таким образом, вся последовательность входных сигналов определяет последовательность состояний автомата и его выходных сигналов. Это объясняет название «последовательностные схемы».
Основным качеством, выделяющим цифровые автоматы из числа всех других преобразователей информации, является наличие дискретного множества внутренних состояний и свойстваскачкообразного перехода автомата из одного состояния в другое. Скачкообразность перехода означает возможность трактовать этот переход как мгновенный, хотя для любого реально существующего автомата имеет место конечная длительность переходных процессов, так что требование скачкообразности перехода не удовлетворяется.
Второе допущение состоит в том, что после перехода автомата в произвольное состояние переход в следующее состояние оказывается возможным не ранее, чем через некоторый фиксированный для данного автомата промежуток времени τ>0, так называемый интервал дискретности автомата. Это допущение дает возможность рассматривать функционирование цифрового автомата вдискретном времени. При построении автоматов с дискретным автоматным временем различаютсинхронные и асинхронные автоматы.
Цифровые автоматы в каноническом представлении разделяют на две части (рис. 5.1): память(ЭП) и комбинационную цепь (КЦ). На входы КЦ подаются входные сигналы Zt и сигналы состояния At цифрового автомата. На ее выходе вырабатываются выходные сигналы Wt и сигналы перевода ЦА в новое состояние At+1.
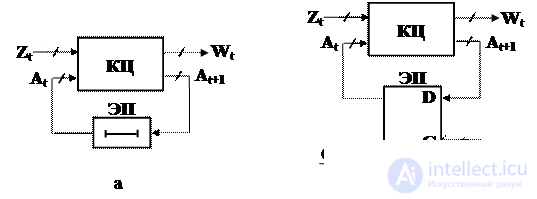
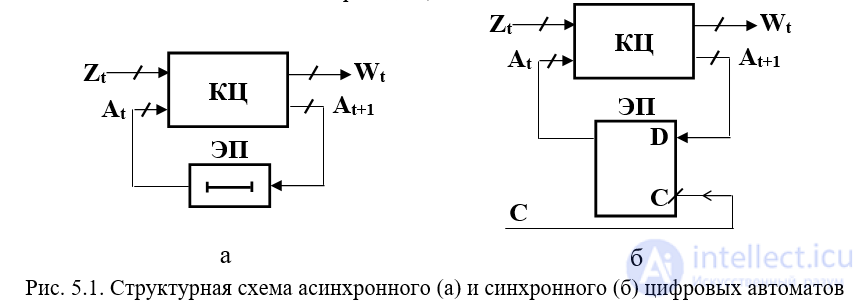
Рис. 5.1. Структурная схема асинхронного (а) и синхронного (б) цифровых автоматов
В асинхронных автоматах (рис. 5.1.а) очень часто роль элементов памяти играют элементызадержки, через которые сигналы состояния Atпередаются на входы КЦ, чтобы совместно с новым набором входных переменных Zt определить следующую пару значений выходов Wt и состоянияAt+1 на выходе. Элементы асинхронного ЦА переключаются под непосредственным воздействием изменений входных сигналов. Скорость распространения процесса переключений в цепях асинхронного автомата определяется собственными задержками элементов, поэтому моменты переходов из одного состояния в другое заранее не определены и могут совершаться через неравные между собой промежутки времени.
В синхронных автоматах имеются специальные входы С для подачи синхросигналов, которые разрешают элементам памяти прием данных только в определенные моменты времени.Элементами памяти (ЭП) в таких автоматах служат синхронные триггеры. Моменты времени, в которые оказывается возможным изменение состояния автомата, определяются специальным устройством – генератором синхронизирующих импульсов, выход которого подключается на входС синхронного автомата. Соседние моменты времени оказываются при этом обычно разделенными равными временными промежутками. Процесс обработки информации в синхронных ЦА упорядочивается во времени, и в течение одного такта возможно распространение процесса переключения только в строго определенных пределах тракта обработки информации.
Общая теория автоматов при сделанных выше допущениях разбивается на две большие части, которым присвоены названия абстрактной теории автоматов и структурной теории автоматов. Различие между ними заключается в том, что в абстрактной теории не учитываются структура как самого автомата, так и структуры его входных и выходных сигналов. Входные и выходные сигналы рассматриваются при этом просто как буквы двух фиксированных для данного автомата алфавитов: входного и выходного. Не интересуясь способом построения автомата, абстрактная теория изучает лишь те переходы, которые претерпевает автомат под воздействием входных сигналов, и те выходные сигналы, которые он при этом выдает.
В противоположность абстрактной теории, структурная теория автоматов учитывает структуры автомата и его входных и выходных сигналов. В структурной теории изучаются способы построения автоматов из нескольких элементарных автоматов, способы кодирования входных и выходных сигналов элементарными сигналами, передаваемыми по реальным входным и выходным каналам.
Таким образом, структурная теория автоматов является продолжением и дальнейшим развитием абстрактной теории. В частности, задача синтеза идеализированного (без учета переходных процессов) цифрового автомата естественным образом подразделяется на этапы абстрактного и структурного синтеза.
Математической моделью ЦА (а в общем случае любого дискретного устройства) является так называемый абстрактный автомат, определенный как 6-компонентный кортеж: S=(A, Z, W, d, l, а1) у которого:
1. A={a1, a2, ... ,am} - множество состояний (внутренний алфавит),
2. Z={z1, z2, ... ,zf} - множество входных сигналов (входной алфавит),
3. W={w1, w2, ..., wg} - множество выходных сигналов (выходной алфавит),
4. d : A·Z®A - функция переходов, реализующая отображение Dd ÍА·Z в А. Иными словами функция d некоторым парам “состояние - входной сигнал” (аm, zf) ставит в соответствие состояния автомата аs= d (am, zf), asÎA,
5. l : A·Z®W - функция выходов, реализующая отображение Dl ÍА·Z на W. Функция l некоторым парам “состояние - входной сигнал” (аm, zf) ставит в соответствие выходные сигналы автомата Wg=l(аm, zf), WgÎW,
6. ai ÎA - начальное состояние автомата.
Под алфавитом здесь понимается непустое множество попарно различных символов. Элементы алфавита называются буквами, а конечная упорядоченная последовательность букв - словомв данном алфавите.
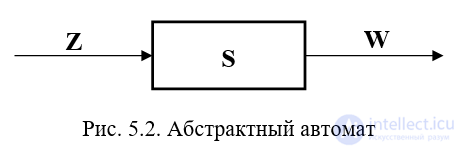
Рис. 5.2. Абстрактный автомат
Абстрактный автомат (рис. 5.2) имеет один вход и один выход. Автомат работает в дискретном времени, принимающем целые неотрицательные значения t = 0,1,2,... В каждый момент t дискретного времени автомат находится в некотором состоянии a(t) из множества состояний автомата, причем в начальный момент t = 0 он всегда находится в начальном состоянии a(0)=a1. В момент t, будучи в состоянии a(t), автомат способен воспринять на входе букву входного алфавита z(t)ÎZ. В соответствии с функцией выходов он выдаст в тот же момент времени t букву выходного алфавита W(t)=l(a(t), z(t)) и в соответствии с функцией переходов перейдет в следующее состояние a(t+1)=d[a(t), z(t)], a(t) ÎA, w(t) ÎW.
Смысл понятия абстрактного автомата состоит в том, что он реализует некоторое отображение множества слов входного алфавита Z во множество слов выходного алфавита W. Т.е. если на вход автомата, установленного в начальное состояние a1, подавать буква за буквой некоторую последовательность букв входного алфавита z(0), z(1),... - входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита w(0), w(1),... - выходное слово. Таким образом, выходное слово = =j(входное слово), где j - отображение, осуществляемое абстрактным автоматом.
На уровне абстрактной теории понятие "работа автомата" понимается как преобразование входных слов в выходные. Можно сказать, что в абстрактном автомате отвлекаемся от его структуры - содержимого прямоугольника (рис. 5.1), рассматривая его как "черный ящик", т.е. основное внимание уделяем поведению автомата относительно внешней среды.
Понятие состояния в определении автомата введено в связи с тем, что часто возникает необходимость в описании поведения систем, выходы которых зависят не только от состояния входов в данный момент времени, но и от некоторой предыстории, т.е. от сигналов, которые поступали на входы системы ранее. Состояния как раз и соответствуют некоторой памяти о прошлом, позволяя устранить время как явную переменную и выразить выходной сигнал как функцию состояния и входа в данный момент времени.
На практике наибольшее распространение получили два класса автоматов - автоматы Мили (Mealy) и Мура (Moore).
Закон функционирования автомата Мили задается уравнениями:
a(t+1) = d(a(t), z(t)); w(t) = l(a(t), z(t)), где t = 0,1,2,...
Закон функционирования автомата Мура задается уравнениями:
a(t+1)=d(a(t), z(t)); w(t) = l(a(t)), где t = 0,1,2,...
Из сравнения законов функционирования видно, что, в отличие от автомата Мили, выходной сигнал в автомате Мура зависит только от текущего состояния автомата и в явном виде не зависит от входного сигнала. Для полного задания автомата Мили или Мура дополнительно к законам функционирования, необходимо указать начальное состояние и определить внутренний, входной и выходной алфавиты.
Кроме автоматов Мили и Мура иногда оказывается удобным пользоваться совмещенной моделью автомата, так называемым С- автоматом.
Под абстрактным С- автоматом будем понимать математическую модель дискретного устройства, определяемую восьмикомпонентным вектором
S=( A, Z, W, U, d, l1, l2, а1 ), у которого:
1. A={a1, a2, ... ,am} - множество состояний;
2. Z={z1, z2, ... ,zf} - входной алфавит;
3. W={w1, w2, ..., wg} - выходной алфавит типа 1;
4. U={u1, u2,...,uh} - выходной алфавит типа 2;
5. d : A · Z ® A - функция переходов, реализующая отображение Dd ÍА·Z в А;
6. l1 : A · Z ® W - функция выходов, реализующая отображение Dl1 ÍА·Z в W;
7. l2 : A ® U - функция выходов, реализующая отображение Dl2 ÍА в U;
8. а1 Î А - начальное состояние автомата.
Абстрактный С-автомат можно представить в виде устройства с одним входом, на который поступают сигналы из входного алфавита Z, и двумя выходами, на которых появляются сигналы из алфавитов W и U. Отличие С-автомата от моделей Мили и Мура состоит в том, что он одновременно реализует две функции выходов l1 и l2, каждая из которых характерна для этих моделей в отдельности. Закон функционирования С- автомата можно описать следующими уравнениями: а( t + 1)=d(a( t), z( t)); w( t)=l1(a( t), z( t)); u( t)=l2(a( t)), где t = 0, 1, 2, ...
Выходной сигнал Uh=l2(am) выдается все время, пока автомат находится в состоянии am. Выходной сигнал Wg=l1(am, zf) выдается во время действия входного сигнала Zf при нахождении автомата в состоянии am.
Рассмотренные выше абстрактные автоматы можно разделить на:
1) полностью определенные и частичные;
2) детерминированные и вероятностные.
Полностью определенным называется абстрактный цифровой автомат , у которого функция переходов и функция выходов определены для всех пар (ai, zj).
Частичным называется абстрактный автомат, у которого функция переходов или функция выходов, или обе эти функции определены не для всех пар (ai, zj).
К детерминированным относятся автоматы, у которых выполнено условие однозначности переходов: автомат, находящийся в некотором состоянии ai, под действием любого входного сигнала zj не может перейти более, чем в одно состояние.
В противном случае это будет вероятностный автомат, в котором при заданном состоянии ai и заданном входном сигнале zj возможен переход с заданной вероятностью в различные состояния.
Абстрактный автомат называется конечным, если конечны множества А = {a1, a2, ..., am}, Z = {z1, z2, ..., zf}, W = {w1, w2, ..., wg}. Автомат носит название инициального, если в нем выделено начальное состояние a1.
Вслед за этапом абстрактного синтеза автоматов следует этап структурного синтеза, целью которого является построение схемы, реализующей автомат из элементов заданного типа. Если абстрактный автомат был лишь математической моделью, проектируемого устройства, то в структурном автомате учитывается структура входных и выходных сигналов автомата, а также его внутренне устройство на уровне логических схем. Основной задачей структурной теории автоматов является разработка общих методов построения структурных схем автоматов.
В отличие от абстрактного автомата, имеющего один вход и один выход (рис. 5.3.а), на которые поступают сигналы во входном и выходят в выходном W={W1,..,WG} алфавитах, структурный автомат (рис. 5.3.б) имеет L входных каналов х1,х2,..,хL и N выходных y1,y2,…,yN на каждом из которых присутствует сигнал структурного алфавита.
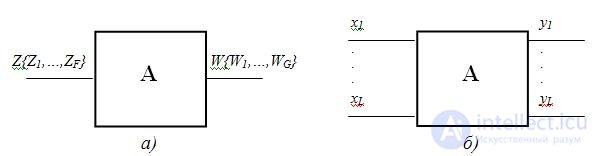
Рис.5.3. Абстрактный (а) и структурный (б) автоматы
Обычно в качестве структурного используется двоичный алфавит. В этом случае каждому входному сигналу ZF абстрактного автомата соответствует некоторый двоичный вектор(lf1,lf2,..,lfL), где lfLÎ{0,1}.
Очевидно, что для представления (кодирования) входных сигналов Z1,..,ZF абстрактного автомата различными двоичными векторами должно быть выполнено условие L 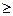 ] log2F [, аналогично N
] log2F [, аналогично N 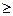 ] log2G [. Например, Z={Z1,Z2,Z3,Z4} и W={W1,W2,W3}, тогда L
] log2G [. Например, Z={Z1,Z2,Z3,Z4} и W={W1,W2,W3}, тогда L 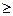 log24=2 и N
log24=2 и N 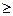 log23=2
log23=2
Закодировать входные и выходные сигналы можно, например, так: Z1 = 00, Z2 = 01, Z3 = 10, Z4= 11, W1 = 00, W2 = 01 и W3 = 11.
Следовательно, структурный автомат с двумя входами x1 и x2 и двумя выходами y1 и y2 может быть представлен в виде, представленном на рис.5.4:
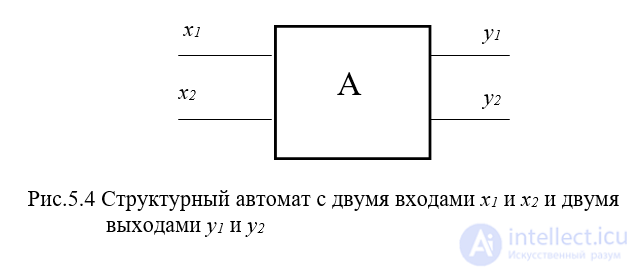
Рис.5.4 Структурный автомат с двумя входами x1 и x2 и двумя выходами y1 и y2
Для того, чтобы задать автомат, необходимо описать все компоненты кортежа S=(A, Z, W, d, l, а1). Множества А, Z, W описываются и задаются простым перечислением своих элементов. Среди многообразия различных способов заданий функций d и l (следовательно и всего автомата в целом) наибольшее распространение получили табличный и графический.
При табличном способе задания автомат Мили описывается с помощью двух таблиц. Одна из них (таблица переходов) задает функцию d, т.е. a(t +1)=d(a(t), z(t)) (табл. 5.1), вторая (таблица выходов) - функцию l, т.е. W(t)=l(a(t), z(t)) ( табл. 5.2).

Каждому столбцу из приведенных таблиц поставлено в соответствие одно состояние из множества А, каждой строке – один входной сигнал из множества Z. На пересечении столбца am и строки zf в табл. 5.1 записывается состояние as, в которое должен перейти автомат из состояния am под действием входного сигнала Zf, т.е. as=d(am, zf). На пересечении столбца am и строки zf в табл. 5.2 записывается выходной сигнал Wg, выдаваемый автоматом в состоянии am при поступлении на вход сигнала zf, т.е. Wg = l(am, zf).
Для приведенных таблиц множества, образующие автомат A={a1, a2, a3,a4}, Z={z1, z2}, W={w1, w2, w3, w4, w5}. Автомат Мили может быть задан одной совмещенной таблицей переходов и выходов (табл. 5.3), в которой каждый элемент as / wg записанный на пересечении столбца am и строки zf, определяется следующим образом: as=d(am, zf); wf=l(am, zf).
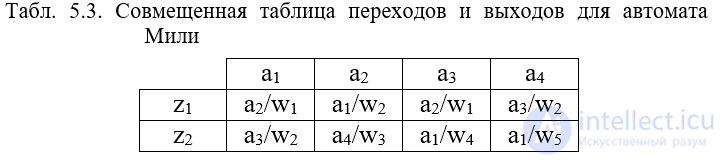
Автомат Мура задается одной отмеченной таблицей переходов (табл. 5.4), в которой каждому столбцу приписаны не только состояние am, но еще и выходной сигнал Wg, соответствующий этому состоянию, где Wg=l(am).
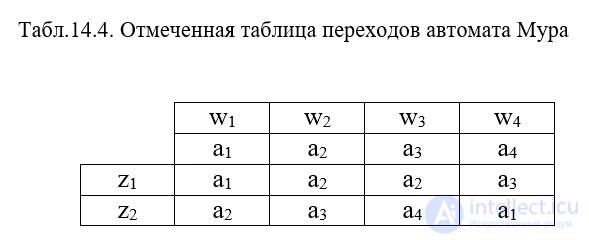
Для частичных автоматов Мили и Мура в рассмотренных таблицах на месте неопределенных состояний и выходных сигналов ставится прочерк. Об этом говорит сайт https://intellect.icu . В таких автоматах выходной сигнал на каком-либо переходе всегда не определен, если неопределенным является состояние перехода. Кроме того, выходной сигнал может быть неопределенным и для некоторых существующих переходов.
Для задания С - автоматов также используется табличный метод. В этом случае таблица переходов (табл.5.5) аналогична таблице переходов автомата Мили, а в таблице выходов каждое состояние отмечено соответствующим выходным сигналом ui выходного алфавита типа 2 (табл.5.6).
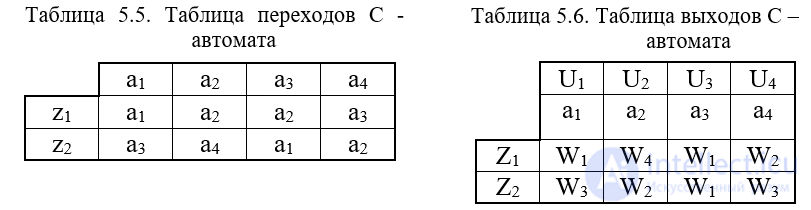
При графическом способе автомат задается в виде ориентированного графа, вершины которого соответствуют состояниям, а дуги - переходам между ними. Дуга, направленная из вершины am, задает переход в автомате из состояния am в состояние as. В начале этой дуги записывается входной сигнал ZfÎZ, вызывающий данный переход as=d(am,zf). Для графа автомата Мили выходной сигнал wgÎW, формируемый на переходе, записывается в конце дуги, а для автомата Мура – рядом с вершиной am, отмеченной состоянием am, в котором он формируется. Если переход в автомате из состояния am в состояние as производится под действием нескольких входных сигналов, то дуге графа, направленной из am в as, приписываются все эти входные и соответствующие выходные сигналы. Граф С-автомата содержит выходные сигналы двух типов и они обозначаются на графе как на графах соответствующих автоматов. Графы автоматов, заданных своими таблицами переходов и выходов (табл. 5.1¸5.6) представлены на рисунках 5.5¸5.7.
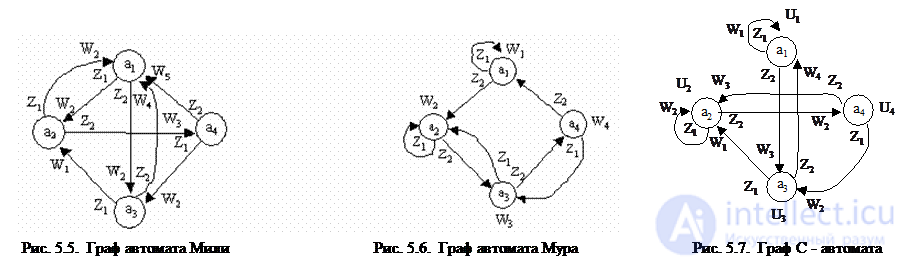
Автоматы Мура, Миля и С-автоматы определяют лишь структуру построения автомата. Автоматы, имеющие разную внутреннюю структуру, могут быть эквивалентны. Два автомата с одинаковыми входными и выходными алфавитами называются эквивалентными, если после установки их в начальное состояние их реакции на любое входное слово совпадают.
Для каждого автомата Мили может быть построен эквивалентный ему автомат Мура и наоборот.( аналогично это относится и к С-автоматам)
Переход от автомата Мура к эквивалентному ему автомату Мили тривиален и легко осуществляется при графическом способе задания автомата. Для получения графа автомата Мили необходимо выходной сигнал Wg, записанный рядом с вершиной as исходного автомата Мура, перенести на все дуги, входящие в эту вершину.
Легко убедиться, что полученный автомат Мили действительно эквивалентный исходному автомату Мура. Для этого достаточно рассмотреть реакцию обеих автоматов на произвольную входную последовательность. Необходимо также отметить, что в эквивалентном автомате Мили количество состояний такое же, как и в исходном автомате Мура.
Переход от автомата Мили к эквивалентному ему автомату Мура более сложен. Это связано с тем, что в автомате Мура в каждом состоянии вырабатывается только один выходной сигнал. Переход наиболее наглядно делать при графическом способе задания автомата. В этом случае каждое состояние ai исходного автомата Мили порождает столько состояний автомата Мура, сколько различных выходных сигналов вырабатывается в исходном автомате при попадании в состояние ai. Рассмотрим переход от автомата Мили Sa к автомату Мура Sb на примере автомата (рис. 5.6).
Как следует из рис. 5.6, для автомата Sa при попадании в состояние а1 вырабатываются выходные сигналы W2, W4, W5, при попадании в а2 – W1, W2, a3 – W2, a4 – W3. Каждой паре „состояние ai- выходной сигнал Wj”, который вырабатывается при попадании в это состояние, поставим в соответствие состояние bk эквивалентного автомата Мура Sb с тем же выходным сигналом Wj : b1=(a1, W2), b2 =(a1, W4), b3 =(a1, W5), b4 =(a2, W1), b5 =(a2, W2), b6 =(a3, W2), b7 =(a4, W3), т.е. каждое состояние ai автомата Мили порождает некоторое множество Ai состояний эквивалентного автомата Мура: A1={b1, b2, b3}, A2={b4, b5}, A3={b6}, A4={b7}. Как видно, в эквивалентном автомате Мура количество состояний 7. Для построения графа Sb поступаем следующим образом. Т.к. в автомате Sa есть переход из состояния а1 в состояние а2 под действием сигнала z1 с выдачей W1, то из множества состояний A1 = {b1, b2, b3}, порождаемых состоянием а1 автомата Sa в автомате Sb должен быть переход в состояние (a3, W2) = b6 под действием сигнала Z2 и т.д. Граф эквивалентного автомата Мура представлен на рис. 5.8.
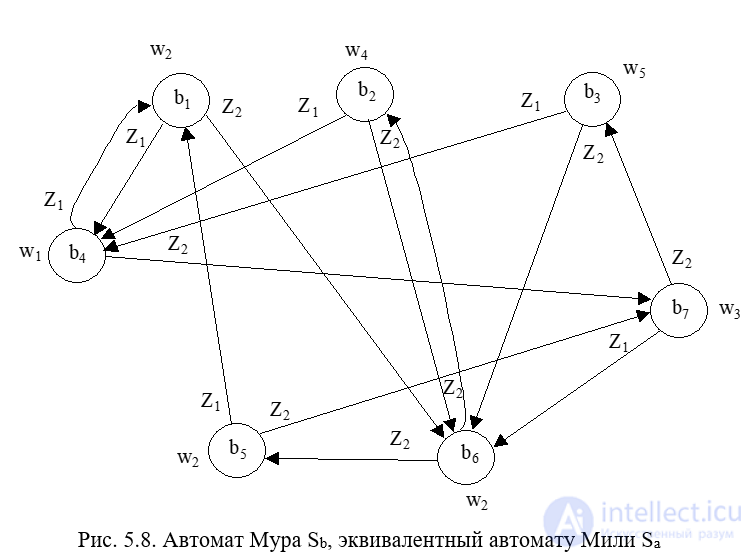
Рис. 5.8. Автомат Мура Sb, эквивалентный автомату Мили Sa
Если от автомата Мура Sb, эквивалентного автомату Мили Sa (рис. 5.8) вновь перейти к автомату Мили, то получим автомат Мили S1 (рис. 5.9).

Рис. 5.9. Автомат Мили S1, эквивалентный автомату Мура Sb
Вследствие транзитивности отношения эквивалентности два автомата Мили S1 и Sa также будут эквивалентными, но у последнего будут на 3 состояния больше. Таким образом, эквивалентные между собой автоматы могут иметь различное число состояний, в связи с чем возникает задача нахождения минимального (т.е. с минимальным числом состояний) автомата в классе эквивалентных между собой автоматов.
Рассмотрим метод минимизации полностью определенных автоматов, предложенный Ауфенкампом и Хоном.
Основная идея этого метода заключается в разбиении всех состояний исходного абстрактного автомата на попарно непересекающиеся классы эквивалентных состояний и замене каждого класса эквивалентности одним состоянием. Т.о. получающийся в результате минимальный автомат имеет столько состояний, на сколько классов эквивалентности разбиваются состояния исходного автомата.
Для пользования методом введем несколько определений.
Два состояния абстрактного автомата называются 1-эквивалентными в том случае, если реакции автомата в этих состояниях на всевозможные входные слова совпадают.
Объединение всех 1-эквивалентных состояний абстрактного автомата образует 1-класс эквивалентности.
1-эквивалентные состояния автомата называются 2-эквивалентными, если они переводятся любым входным сигналом также в 1-эквивалентные состояния.
Объединение всех 2-эквивалентных состояний образует 2-класс эквивалентности.
По индукции можно распространить определение до i-эквивалентных состояний и i-классов эквивалентности.
Если для некоторого i разбиения состояний автомата на ( i +1) - классы совпадает с разбиением на i-классы, то оно является разбиением и на ¥ - классы эквивалентности.
Разбиение множества внутренних состояний автомата на ¥ - классы и является требуемым разбиением на классы эквивалентности, при этом такое разбиение может быть получено за конечное число шагов.
Все вышеизложенное непосредственно применимо к минимизации автомата Мили. При минимизации полностью определенных автоматов Мура вводится понятие 0-эквивалентности состояний и разбиение множества состояний на 0-эквивалентные классы: к такому классу относятся одинаково отмеченные состояния автомата Мура.
Если два 0-эквивалентных состояния любым входным сигналом переводится в два 0-эквивалентных состояния, то они называются 1-эквивалентными. Все дальнейшие классы эквивалентности состояний для автомата Мура определяются аналогично приведенному для автоматов Мили.
Рассмотрим пример минимизации автомата Мили, заданного таблицами переходов и выходов – таблицы 5.7.
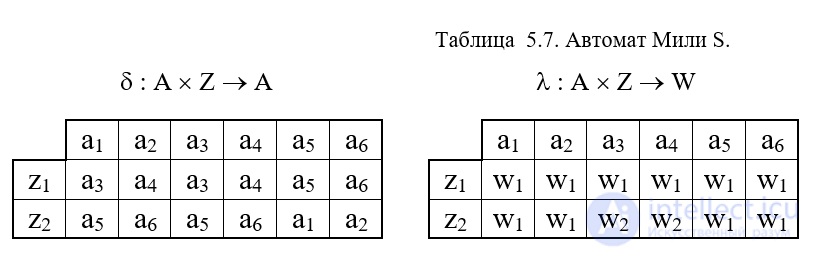
Из таблицы выходов получаем разбиение на 1-классы эквивалентности p1, объединяя в эквивалентные классы Bi состояния с одинаковыми столбцами: p1 = {B1, B2}; B2 = {a1, a2, a5, a6}; B2 = {a3, a4}. Для получения 2-эквивалентных состояний строим таблицу 1-разбиения (табл.5.8), заменяя в таблице переходов состояния a1 соответствующими классами эквивалентности B1 или B2.

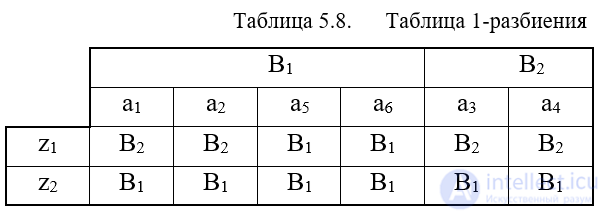
Из полученной таблицы 1-разбиения получаем 2-классы эквивалентности Ci и разбиение p2 = {C1, C2, C3}, где С1 = {a1, a2}, C2 = {a5, a6}, C3 = {a3, a4}. Сравнивая p2 и p1, отмечаем, что эти разбиения отличаются друг от друга. Поэтому аналогично строим таблицу 2-разбиения (табл. 5.9), опять заменяя в таблице переходов состояния ai соответствующими классами эквивалентности Ci.

Из полученной таблицы 2-разбиения получаем 3-классы эквивалентности Di и разбиение p3 ={ D1, D2, D3}, где D1 = {a1, a2}, D2 = {a5, a6}, D3 = {a3, a4}.
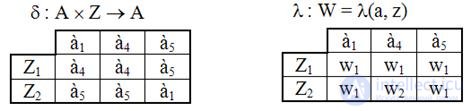
Сравнивая p3 и p2, замечаем, что D1 = C1, D2 = C2, D3 = C3, p3 = p3. Следовательно получили разбиение на ¥- эквивалентные классы. Т.к. всего три таких класса, то минимальный автомат будет содержать всего три состояния. Выбираем из каждого класса Di по одному состоянию и получаем множество состояний A' минимального автомата. Пусть, например, A'={à1, à4, à5}. Для получения минимального автомата из первоначальных таблиц переходов и выходов (табл. 5.7) вычеркиваем столбцы, соответствующие "лишним состояниям" a2, a3, a6. В результате получается минимальный автомат Мили, эквивалентный исходному автомату (табл. 5.10).
Табл.5.10. Таблицы переходов и выходов минимального автомата
Минимизацией числа внутренних состояний автомата заканчивается этап абстрактного синтеза.
ЭВМ перерабатывает информацию, выполняя над ней какие-то операции. Для выполнения операций над информацией используются операционные устройства – процессоры, каналы ввода-вывода, устройства управления внешними устройствами и т.д. Функцией операционного устройства является выполнение заданного множества операций F={f1,...,fG} над входными словами D={d1,...,dH} c целью вычисления слов R={r1,...,rQ}, которые представляют результаты операцийR=fg(D), где g=1,2,...,G.
Функциональная и структурная организация операционных устройств базируется на принципе микропрограммного управления, который состоит в следующем:
1. Любая операция fg (g=1,...,G), реализуемая устройством, рассматривается как сложное действие, которое разделяется на последовательность элементарных действий над словами информации. Эти элементарные действия называются микрооперациями.
2. Для управления порядком следования микроопераций используются логические условия, которые в зависимости от значений слов, преобразуемых микрооперациями, принимают значения "ложь" или "истина" (1 или 0).
3. Процесс выполнения операций в устройстве описывается в форме алгоритма, который представляется в терминах микроопераций и логических условий и
продолжение следует...
Часть 1 Тема 5. Схемотехника цифровых узлов, Цифровые автоматы и их разновидности
Часть 2 Операционные элементы - Тема 5. Схемотехника цифровых узлов, Цифровые автоматы
Часть 3 Вау!! 😲 Ты еще не читал? Это зря! - Тема 5. Схемотехника цифровых узлов, Цифровые автоматы
Надеюсь, эта статья про схемотехника цифровых узлов, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое схемотехника цифровых узлов, цифровой автомат и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Компьютерная схемотехника и архитектура компьютеров
Комментарии
Оставить комментарий
Компьютерная схемотехника и архитектура компьютеров
Термины: Компьютерная схемотехника и архитектура компьютеров