Лекция
Привет, сегодня поговорим про абстрактный автомат, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое абстрактный автомат, методы задания автоматов, классификация абстрактных автоматов , настоятельно рекомендую прочитать все из категории Теория автоматов.
Простейший преобразователь информации (рис.1.1,а) отображает некоторое множество элементов информации Х, поступающее на вход, в некоторое множество на выходе Y. Если множества Х и Y являются конечными и дискретными, то есть преобразование осуществляется в дискретные моменты времени, то такие преобразователи информации называются конечными преобразователями. Элементы множеств Х и Y в этом случае предварительно кодируют двоичными кодами и строят преобразование одного множества в другое.
абстрактный автомат (в теории алгоритмов) — математическая абстракция, модель дискретного устройства, имеющего один вход, один выход и в каждый момент времени находящегося в одном состоянии из множества возможных. На вход этому устройству поступают символы одного алфавита, на выходе оно выдает символы (в общем случае) другого алфавита.
Формально абстрактный автомат определяется как пятерка
Где S — конечное множество состояний автомата, X, Y — конечные входной и выходной алфавиты соответственно, из которых формируются строки, считываемые и выдаваемые автоматом, 
— функция переходов, 
— функция выходов.
Абстрактный автомат с выделенным начальным состоянием называется инициальным автоматом. Таким образом, абстрактный автомат определяет семейство инициальных автоматов
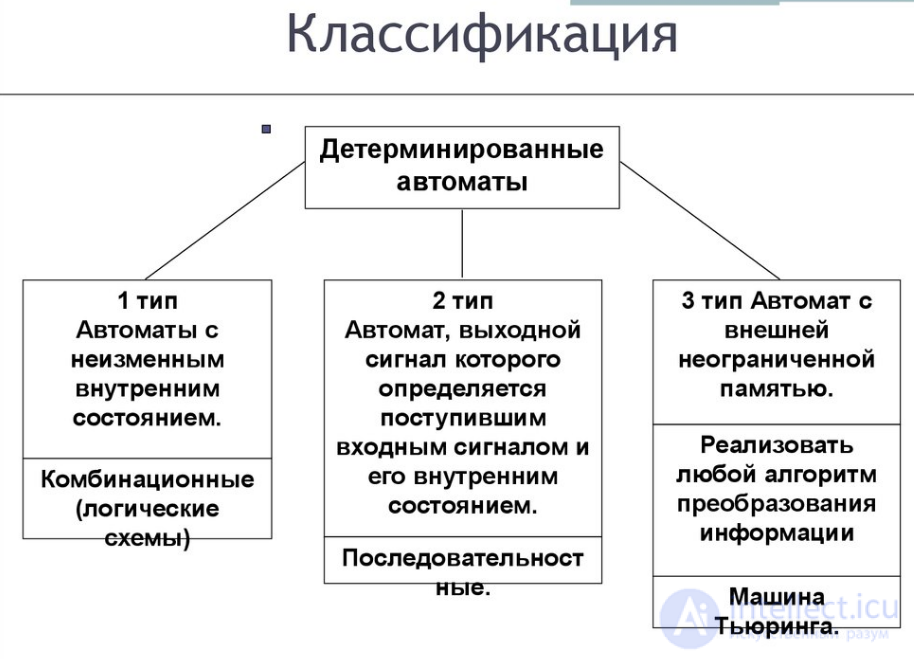
Если функции переходов и выходов однозначно определены для каждой пары 
, то автомат называют детерминированным. В противном случае автомат называют недетерминированным или частично определенным.
Если функция переходов и/или функция выходов являются случайными, то автомат называют вероятностным.
Ограничение числа состояний абстрактного автомата определило такое понятие как конечный автомат.
Функционирование автомата состоит в порождении двух последовательностей: последовательности очередных состояний автомата 
и последовательности выходных символов 
, которые для последовательности символов 
разворачиваются в моменты дискретного времени t = 1, 2, 3, … Моменты дискретного времени получили название тактов.
Функционирование автомата в дискретные моменты времени t может быть описано системой рекуррентных соотношений: 
Для уточнения свойств абстрактных автоматов введена классификация.
Абстрактные автоматы образуют фундаментальный класс дискретных моделей как самостоятельная модель, и как основная компонента машин Тьюринга, автоматов с магазинной памятью, конечных автоматов и других преобразователей информации.
Модель абстрактного автомата широко используется, как базовая, для построения дискретных моделей автоматов, распознающих, порождающих и преобразующих последовательности символов.
Существует более общий класс математических объектов. Основной задачей распознавателя является определение того, принадлежит ли заданная строка языку, соответствующему распознавателю. В то же время часть возникает задача не распознавания строки, а ее преобразования в другой вид.
Частным случаем может служить распознавание строки, которое можно рассматривать как преобразование произвольного символа в два символа "да" и "нет", где символ "да" означает, что строка принадлежит заданному языку.
Типичным примером преобразования является трансляция какой-либо программы с языка высокого уровня на язык машинных кодов и задача преобразования математических выражений.
Понятие абстрактного автомата является наиболее общим. И фактически большинство видов автоматов являются частным случаем абстрактного автомата. В целом иерархия автоматов может быть представлена в соответствии с рисунком 3.
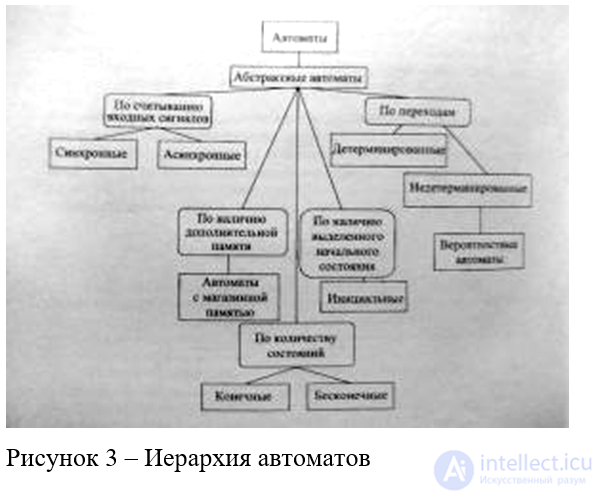
Рисунок 3 - Иерархия автоматов
Ниже в тексте используются следующие обозначения:
— множество состояний автомата
— входной алфавит
— выходной алфавит
— функция переходов
— функция выходов
, , — конечные непустые множества
По способу формирования функций выходов выделяют автоматы Мили и Мура.
В автомате Мили (англ. Mealy machine) функция выходов определяет значение выходного символа по классической схеме абстрактного автомата. Математическая модель автомата Мили и схема рекуррентных соотношений не отличаются от математической модели и схемы рекуррентных соотношений абстрактного автомата. Таким образом, можно дать следующее определение:
Конечным детерминированным автоматом типа Мили называется совокупность пяти объектов
,
где , и — конечные непустые множества, а и — отображения вида:
и
со связью элементов множеств , и в абстрактном времени 
= 0, 1, 2, … уравнениями:
(Отображения и получили названия, соответственно функции переходов и функции выходов автомата A).
Особенностью автомата Мили является то, что функция выходов является двухаргументной и символ в выходном канале 
обнаруживается только при наличии символа во входном канале 
. Об этом говорит сайт https://intellect.icu . Функциональная схема не отличается от схемы абстрактного автомата.
Зависимость выходного сигнала только от состояния представлена в автоматах типа Мура (англ. Moore machine). В автомате Мура функция выходов определяет значение выходного символа только по одному аргументу — состоянию автомата. Эту функцию называют также функцией меток, так как она каждому состоянию автомата ставит метку на выходе.
Конечным детерминированным автоматом типа Мура называется совокупность пяти объектов: 
где , , и — соответствуют определению автомата типа Мили, а 
является отображением вида: μ : S → Y,
с зависимостью состояний и выходных сигналов во времени уравнением:
.
Особенностью автомата Мура является то, что символ в выходном канале существует все время, пока автомат находится в состоянии 
.
Для любого автомата Мура существует автомат Мили, реализующий ту же самую функцию. И наоборот: для любого автомата Мили существует соответствующий автомат Мура (возможно, со сдвигом по времени, т.е. 
)
Интересно выделить особые классы автоматов, математические модели которых опираются только на два носителя алгебры.
Пусть |X| = 1. Тогда математическая модель и система рекуррентных соотношений имеют вид:
,
где и — конечные непустые множества состояний и выходных сигналов, а 
и 
— отображения выше указанного вида.
Особенностью функционирования такого автомата является генерация последовательности символов выходного слова только в зависимости от последовательности состояний автомата.
Такой автомат получил название автономного конечного детерминированного автомата.
Для каждых начального состояния 
и натурального числа 
автомат B определяет две последовательности:
Конечный автомат может быть представлен как преобразователь входных последовательностей в выходные. При этом выходные последовательности могут рассматриваться как порождаемые, а входные — как представляемые. Выходные последовательности автомата определяют множество слов, порождаемых этим автоматом. Автономный КДА называется порождающим, если порождаемое им слово представлено как выходная последовательность, при этом такая последовательность называется порождаемой данным автоматом.
Пусть 
. Тогда математическая модель и система рекуррентных соотношений имеют вид:
По характеру отсчета дискретного времени автоматы делятся на синхронные и асинхронные.
В синхронных конечных автоматах моменты времени, в которые автомат считывает входные сигналы, определяются принудительно синхронизирующими сигналами. После очередного синхронизирующего сигнала с учетом «считанного» и в соответствии с соотношениями для функционирования автомата происходит переход в новое состояние и выдача сигнала на выходе, после чего автомат может воспринимать следующее значение входного сигнала.
Асинхронный конечный автомат считывает входной сигнал непрерывно, и поэтому, реагируя на достаточно длинный входной сигнал постоянной величины x, он может, как следует из соотношений для функционирования автомата, несколько раз изменять состояние, выдавая соответствующее число выходных сигналов, пока не перейдет в устойчивое состояние, которое уже не может быть изменено данным входным сигналом.
Абстрактный автомат - математический объект, представляющий собой совокупность элементов: A=(S,X,Y,д,л), где S - конечное множество состояний автомата; X,Y - конечные входной и выходной алфавиты соответственно, из которых формируются строки, считываемые и выдаваемые автоматом; д:SxY->S - переходное отношение (переходная функция); л - выходная функция.
Абстрактный автомат имеет следующую функциональную схему, в соответствии с рисунком 2.
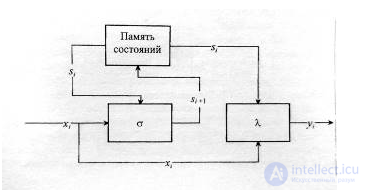
Рисунок 2 - Функциональная схема абстрактного автомата
Где si - новое состояние автомата; xi - текущий входной символ; yi - текущий выходной символ.
Порядок работы абстрактного автомата следующий:
Объемом памяти абстрактного автомата называют количестве его внутренних состояний.
Следует отметить, что способы задания автоматов аналогичны способам задания распознавателей - это таблица переходов и диаграмма переходов. математика дискретный автомат
Результат преобразования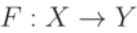 
зачастую зависит не только от того, какая информация в данный момент появилась на входе, но и от того, что происходило раньше, то есть от предыстории преобразования. Например, один и тот же вход - извинение соседа после того, как он вам наступил на ногу в переполненном автобусе - вызовет у вас одну реакцию в первый раз и совсем другую - в пятый раз.
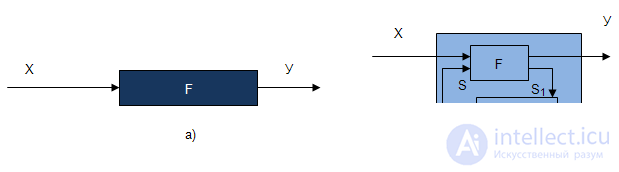
Таким образом, существуют более сложные преобразователи информации (ПИ), реакция которых зависит не только от входных сигналов в данный момент, но и от того, что было раньше, от входной истории. Такие ПИ называются автоматами (схемами с памятью). В этом случае говорят об автоматном преобразовании информации (рис.1.1,б). На один и тот же входной сигнал автоматможет реагировать по-разному, в зависимости от состояния, в котором он находился. Автомат меняет свое состояние с каждым входным сигналом.
Рассмотрим несколько примеров.
Пример 11. Автомат, описывающий поведение "умного" отца.
Опишем поведение отца, дочь которого учится в школе и приносит двойки и пятерки. Отец не хочет хвататься за ремень каждый раз, как только дочь получит двойку, и выбирает более тонкую тактику воспитания. Зададим такой автомат графом, в котором вершины соответствуют состояниям, а дуга из состояния s в состояние q, помеченное x/y, проводится тогда, когда автомат из состояния s под воздействием входного сигнала х переходит в состояние q с выходной реакцией y. Граф автомата, моделирующего умное поведение родителя, представлен на рис.1.2. Этот автомат имеет четыре состояния 
, два входных сигнала - оценки 
и выходные сигналы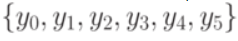 
, которые будем интерпретировать как действия родителя следующим образом:
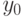- брать ремень;
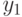- ругать дочь ;
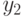- успокаивать дочь ;
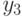- надеяться;
- радоваться;
- ликовать.
дочь , получившего одну и ту же оценку - двойку, ожидает дома совершенно различная реакция отца в зависимости от предыстории его учебы. Например, после третьей двойки в истории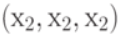 
дочь встретят ремнем, а в истории 
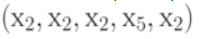будут успокаивать и т.д.
Конечный автомат может быть реализован как программно, так и аппаратно. Программную реализацию можно выполнить на любомязыке высокого уровня разными способами. На рис.1.3 представлена блок-схема программы, реализующей поведение автоматапримера 1. Нетрудно увидеть, что топология блок-схемы программы повторяет топологию графа переходов автомата. С каждым состоянием связана операция NEXT, выполняющая функцию ожидания очередного события прихода нового входного сигнала и чтения его в некоторый стандартный буфер х, а также последующий анализ того, какой это сигнал. В зависимости от того, какой сигнал пришел на вход, выполняется та или иная функция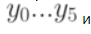 
и происходит переход к новому состоянию.
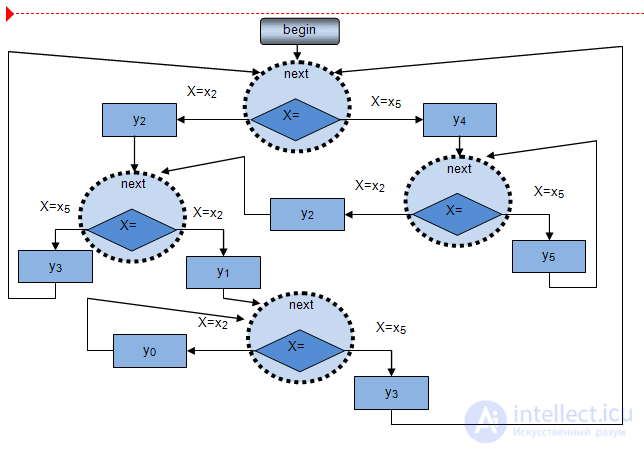
Аппаратную реализацию автомата рассмотрим во второй части этого раздела.
Пример 2. "Студент"
Автомат, модель которого представлена на рис.1.4, описывает поведение студента и преподавателей.
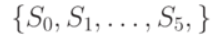- состояния;
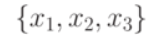- входные сигналы: "н", "2" и "5".
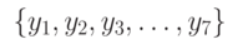- выходные реакции:
Пример 31. Электронные часы (рис.1.5).
Электронные часы разнообразных функциональных возможностей являются одним из наиболее широко применяемых в быту электронных приборов, управление которыми построено на основе конечноавтоматной модели. Они обычно показывают: время, дату; у них имеется функции такие как "установка времени и даты", "Секундомер", "Будильник"и т.п. Упрощенная структурная схемаэлектронных часов показана нарис.1.5
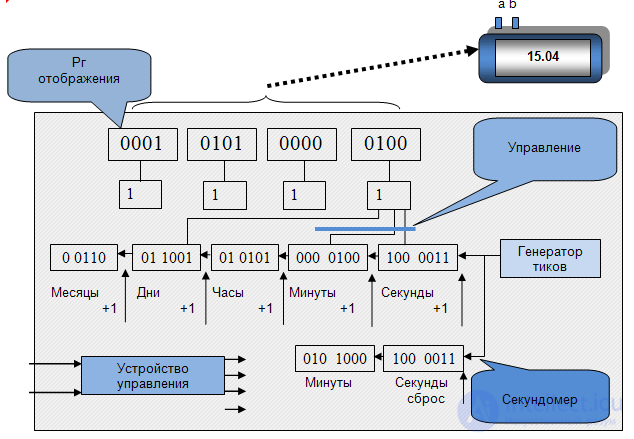
Регистры отображают либо время, либо дату, либо секундомер в зависимости от "Управления". Устройство управления построено на основе модели конечного автомата. Конечный автомат реагирует на нажатия кнопки "а" на корпусе переходом в состояние "Установка минут", в котором событие нажатия кнопки "b" вызовет увеличение числа. Устройство управления построено на основе модели конечного автомата, граф которого показан нарис.1.6
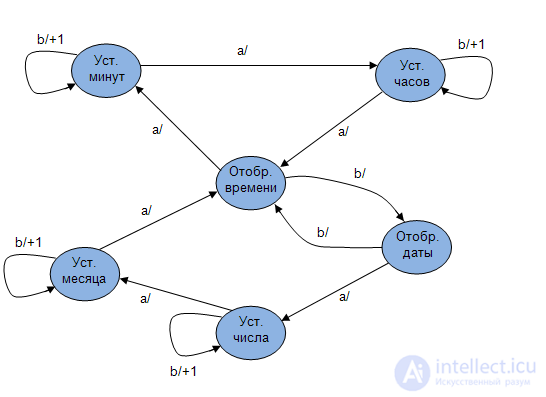
Итак. С одной стороны АВТОМАТ - устройство, выполняющее некоторые действия без участия человека. С другой стороны, АВТОМАТ- математическая модель, описывающая поведение технического устройства. В данном случае реальное устройство, система и т.д. рассматривается как некоторый "ЧЁРНЫЙ ЯЩИК" (рис.1.7).
Абстрактный автомат - это математическая модель, описывающая техническое устройство совокупностью входных, выходных сигналов и состояний, кроме того:
, называемых состояниями автомата;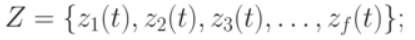
имеется конечное множество выходных сигналов 
;
;
;
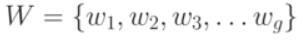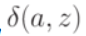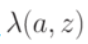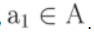.То есть для описания автомата нужно использовать шестерку вида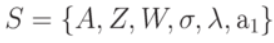 
, где
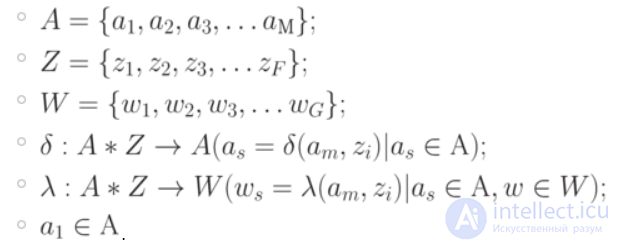
Автомат реализует некоторое отображение множества слов входного алфавита Z в множество слов выходного алфавита W.
Автомат называется конечным, если множество его внутренних состояний и множество значений входных сигналов есть конечные множества.
Автомат называется синхронным, если интервал временной дискретизации постоянен, в противном случае говорят об асинхронном автомате.
Автомат называется детерминированным, если поведение автомата в каждый момент времени однозначно определено (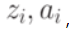 
,)
В зависимости от способа определения выходного сигнала в синхронных автоматах различают:
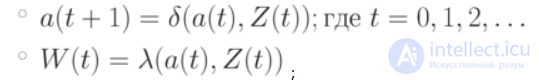
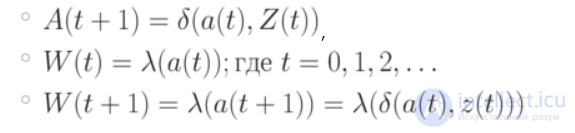
Для задания конечного автомата S требуется описать все элементы множества
наиболее часто используемой формой описания элементов множества S используется табличный, графический, матричный способы.
Для задания конечного автомата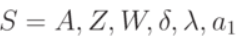 
все элементы множества должны быть заданы явно. Так дляавтомата Мили:
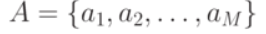- алфавит состояний;
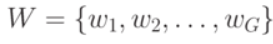- выходной алфавит;
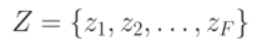- входной алфавит;
- начальное состояние автомата.
Например, автомат Мили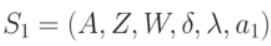 
, представленный в табл.1.3 в явной форме описывается так:
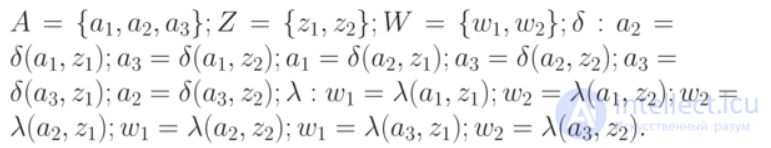
Автомат Мура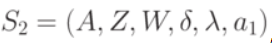 
, представленный в табл.1.8 в явной форме описывается так:
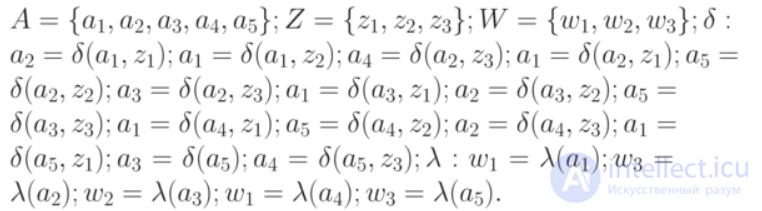
Табличная форма для автомата Мили иллюстрируется табл.1.1 (переходов) и табл.1.2 (выходов).
табл.1.2 (выходов).
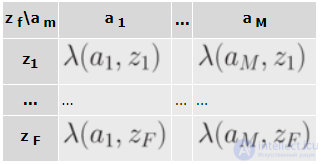
Строки этих таблиц соответствуют входным сигналам, а столбцы - состояниям, причем крайний левый столбец обозначен начальным состоянием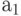 
. На пересечении столбца 
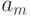и строки 
…. в таблице переходов ставится функция перехода 
, то есть состояние, в которое автомат переходит из состояния 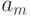под действием входного сигнала 
а в таблице выходов - выходная функция 
, то есть соответствующий этому переходу выходной сигнал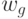 
.
Пример табличного способа задания автомата Мили показан в табл. 1.3 (переходов) и табл. 1.4 (выходов).
| z f \a m | a1 | a2 | a3 |
|---|---|---|---|
| z1 | a2 | a1 | a3 |
| z2 | a3 | a3 | a2 |
| z f \a m | a1 | a2 | a3 |
|---|---|---|---|
| z1 | w1 | w2 | w1 |
| z2 | w2 | w2 | w2 |
Автомат называется частично заданным, если он определен не для всех пар переходов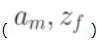 
. Для частично заданногоавтомата на месте отсутствующего перехода ставится прочерк как в таблице переходов, так и в таблице выходов.
Пример табличного способа задания частичного автомата показан в табл.1.5 (переходов) и табл.1.6 (выходов).
| z f\ a m | a 1 | a2 | a 3 | a 4 |
|---|---|---|---|---|
| z1 | a 2 | a 1 | a 3 | - |
| z2 | a 3 | a 3 | a - | a 1 |
| z3 | - | a4 | a2 | a4 |
| z f\ a m | a 1 | a2 | a 3 | a 4 |
|---|---|---|---|---|
| z1 | w1 | w 2 | w 1 | - |
| z2 | w 2 | w1 | - | w 2 |
| z3 | - | w1 | w2 | w1 |
Табличная форма задания автомата Мура представляет собой совмещенную табл.1.7, в которой выходной сигнал, соответствующий состоянию в 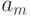автомате Мура размещен в верхней строке над соответствующими состоянием, а остальная информация аналогична представлению автомата Мили.
Пример представления автомата Мура приведен в табл.1.8.
Таблица 1.7.
| \ wG | w1 | w3 | w2 | w1 | w3 |
|---|---|---|---|---|---|
| zf\ am | a 1 | a2 | a3 | a4 | a5 |
| z1 | a2 | a1 | a1 | a1 | a1 |
| z2 | a3 | a5 | a2 | a5 | a3 |
| z3 | a4 | a3 | a5 | a2 | a4 |
В данном случае автомат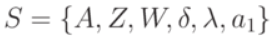 
представляется графом, в котором:
изображено вершинами графа;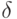
задана дугами графа, причем две вершины графа 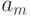и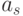 
, соединяются дугой, если в автомате существует переход из 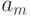в ;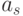
изображено метками дуг: ставится на дуге из вершины 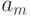в вершину 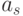, если в автомате существует переход из 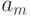в 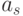под действием входного сигнала ;
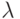задана метками дуг или вершин: для автомата Мили дуга из вершины 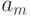в вершину 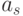помечается выходным сигналом 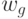, если в автомате существует переход из 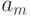в 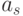и при этом вырабатывается выходной сигнал 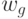; а дляавтомата Мура выходным сигналом 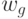помечается вершина, определяющая 
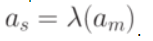.На рисунке 1.8 приведены примеры описания автомата Мили и автомата Мура:
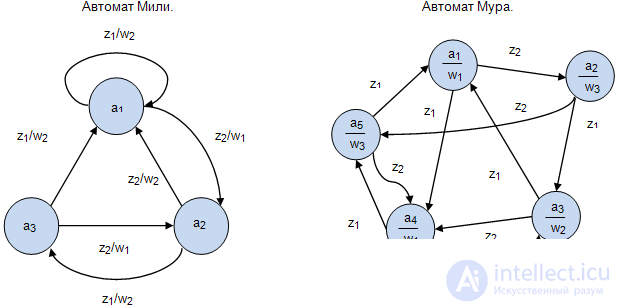
Для автомата Мили матричная форма состоит из матрицы 
размерностью 
, где каждый элементматрицы 
стоящий на пересечении 
-ой строки и 
-го столбца соответствует входному сигналу , вызывающему переход из состояния 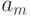в состояние 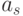с выработкой выходного сигнала 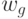. Пример матричного описанияавтомата Мили показан ниже.
Для автомата Мура матричная форма состоит из матрицы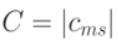 
размерностью , где каждый элементматрицы 
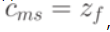, стоящий на пересечении -ой строки и -го столбца, соответствует входному сигналу , вызывающему переход из состояния 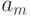в состояние 
Так как выходной сигнал 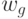. в автомате Мура зависит только от состояния, следовательно, выходные сигналы могут быть представлены матрицей-столбцом. Пример матричного описания автомата Мура показан на формуле, приведенной выше.
Надеюсь, эта статья про абстрактный автомат, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое абстрактный автомат, методы задания автоматов, классификация абстрактных автоматов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория автоматов
Комментарии
Оставить комментарий
Теория цифровых автоматов
Термины: Теория цифровых автоматов