Машина Поста - как вычислительная машина

Привет, Вы узнаете о том , что такое машина поста, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое машина поста , настоятельно рекомендую прочитать все из категории Теория цифровых автоматов.

машина поста (МП) — абстрактная вычислительная машина, предложенная Эмилем Леоном Постом (англ. Emil Leon Post), которая отличается от машины Тьюрингабольшей простотой. Обе машины алгоритмически «эквивалентны» и были придуманы для уточнения понятия «алгоритм». В 1936 г. американский математик Эмиль Пост в статье описал систему, обладающую алгоритмической простотой и способную определять, является ли та или иная задача алгоритмически разрешимой. Если задача имеет алгоритмическое решение, то она представима также в форме последовательности команд для машины Поста.

Машина Поста – это абстрактная (несуществующая реально) вычислительная машина, созданная для уточнения (формализации) понятия алгоритма. Представляет собой универсальный исполнитель, позволяющий вводить начальные данные и читать результат выполнения программы.

В 1936 г. американский математик Эмиль Пост в статье описал систему, обладающую алгоритмической простотой и способную определять, является ли та или иная задача алгоритмически разрешимой.
Если задача имеет алгоритмическое решение, то она представима в форме команд для машины Поста.

В каждой ячейке ленты может быть либо ничего не записано, либо стоять метка V. Информация о том, какие ячейки пусты, а какие содержат метки, образует состояние ленты. Состояние ленты меняется в процессе работы машины.
Заметим, что наличие метки в ячейке можно интерпретировать как “1”, а отсутствие — “0”. Такое двоичное представление информации подобно представлению, используемому практически во всех современных ЭВМ.
Каретка может передвигаться вдоль ленты влево и вправо. Когда она неподвижна, она стоит против ровно одной ячейки ленты.
За единицу времени каретка может совершить одно из трех действий:
- стереть метку,
- поставить метку,
- совершить движение на соседнюю ячейку.

Состояние машины Поста складывается из состояния ленты и положения каретки.

Пост предположил, что любой алгоритм может быть записан как программа для машины Поста.
В теории алгоритмов доказано, что машины Поста и Тьюринга одинаковы по своим возможностям. Это значит, что круг задач, который они решают, тоже одинаков.

Принцип работы

Машина Поста состоит из каретки (или считывающей и записывающей головки) и разбитой на ячейки бесконечной в обе стороны ленты (см. пример ниже). Каждая ячейка ленты может находиться в 2 состояниях — быть либо пустой — 0, либо помеченной меткой 1. За такт работы машины каретка может сдвинуться на одну позицию влево или вправо, считать, изменить символ в своей текущей позиции.

Работа машины Поста определяется программой, состоящей из конечного числа строк. Для работы машины нужно задать программу и ее начальное состояние (то есть состояние ленты и позицию каретки). Кареткой управляет программа, состоящая из пронумерованных не обязательно упорядоченных строк команд, если в каждой команде указана строка, на которую нужно перейти. Обычно принимается, что если в команде переход не указан, то переход происходит на следующую строку. Каждая команда имеет следующий синтаксис:

    i. K j

где i — номер команды, K — действие каретки, j — номер следующей команды (отсылка).

Всего для машины Поста существует шесть типов команд:

   V j      - поставить метку, перейти к j-й строке программы.
   X j      - стереть метку, перейти к j-й строке программы.
   ← j      - сдвинуться влево, перейти к j-й строке программы.
   → j      - сдвинуться вправо, перейти к j-й строке программы.
   ? j1; j2 - если в ячейке нет метки, то перейти к j1-й строке программы, иначе перейти к j2-й строке программы.
   !        – конец программы (стоп).

В команде «стоп» переход на следующую строку не указывается.

После программы запуска возможны варианты:

• работа может закончиться невыполнимой командой (стирание несуществующей метки или запись в помеченное поле);
• работа может закончиться командой Stop;
• работа никогда не закончится.

Пример прибавление единицы к числу

Примеры: сложение и вычитание натуральных чисел P, Q

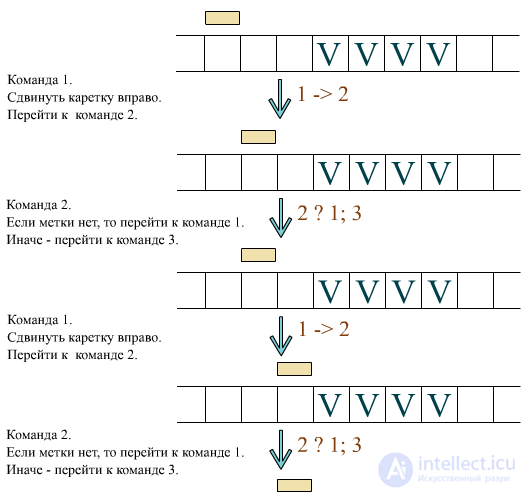
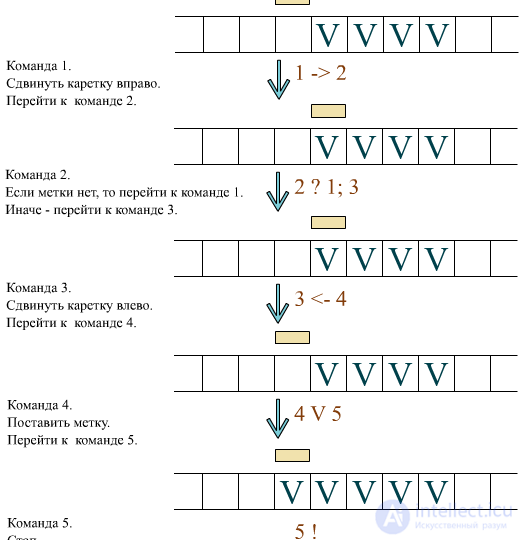
Пусть натуральные (целые неотрицательные) числа P и Q изображаются набором из P и Q единиц и разделены нулем. Пусть исходное положение каретки находится на крайней левой «1» группы единиц Q (помечено символом «v»).

            v
 ...00111110111000...
      ----- ---
        P    Q

Сложение двух чисел тривиально — достаточно поставить 1 между ними и стереть одно крайнее правое «1» у Q. Об этом говорит сайт https://intellect.icu . Программа вычитания состоит из последовательного изменения крайних левых «1» у последовательности «1» в изображении Q и правых «1» у последовательности «1» в изображении P. В начале программы каретка установлена на крайнюю левую «1» у Q:

1. ←       - шаг влево
2. ? 1, 3  - если в ячейке пусто, перейти к 1 шагу, если нет, к 3
3. 0       - удалить метку
4. →       - шаг вправо
5. ? 4, 6  - если в ячейке пусто, перейти к 4 шагу, если нет, к 6
6. 0       - удалить метку
7. →       - шаг вправо
8. ? 9, 1  - если в ячейке пусто, перейти к 9 шагу, если нет, к 1
9. !       - конец

Отметим, что номер команды перехода не указывается, если переход происходит на следующую по порядку строку (для наглядности текста). В 6-й строке возможно зацикливание, если Q > P.

Абстрактные (т.е. существующие не реально, а лишь в воображении) машины Поста и Тьюринга, предназначенные для доказательств различных утверждений о свойствах программ для них, были предложены независимо друг от друга (и практически одновременно) в 1936 г. американским математиком Эмилем Постом и английским математиком Алланом Тьюрингом. Эти машины представляют собой универсальных исполнителей, являющихся полностью детерминированными, позволяющих «вводить» начальные данные, и после выполнения программ «читать» результат. Машина Поста менее популярна, хотя она значительно проще машины Тьюринга. С ее помощью можно вести обучение первым навыкам составления программ для ЭВМ.

Абстрактная машина Поста представляет собой бесконечную ленту, разделенную на одинаковые клетки, каждая из которых может быть либо пустой, либо заполненной меткой «V», и головки, которая может перемещаться вдоль ленты на одну клетку вправо или влево, наносить в клетку ленты метку, если этой метки там ранее не было, стирать метку, если она была, или проверять наличие в клетке метки. Информация о заполненных метками клетках ленты характеризует состояние ленты, которое может меняться в процессе работы машины. В каждый момент времени головка («-») находится над одной из клеток ленты и, как говорят, обозревает ее. Информация о местоположения головки вместе с состоянием ленты характеризует состояние машины Поста, рис.1.16.

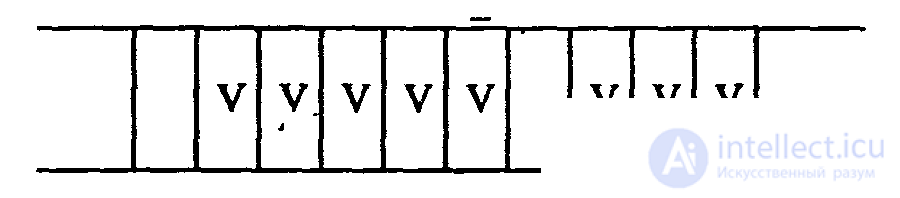
Рис.1.16. Абстрактная машина Поста

Команда машины Поста имеет следующую структуру:

п Km,

где п - порядковый номер команды, K-действие, выполняемое головкой, т - номер следующей команды, подлежащей выполнению.

Существует всего шесть команд машины Поста, рис.1.17:

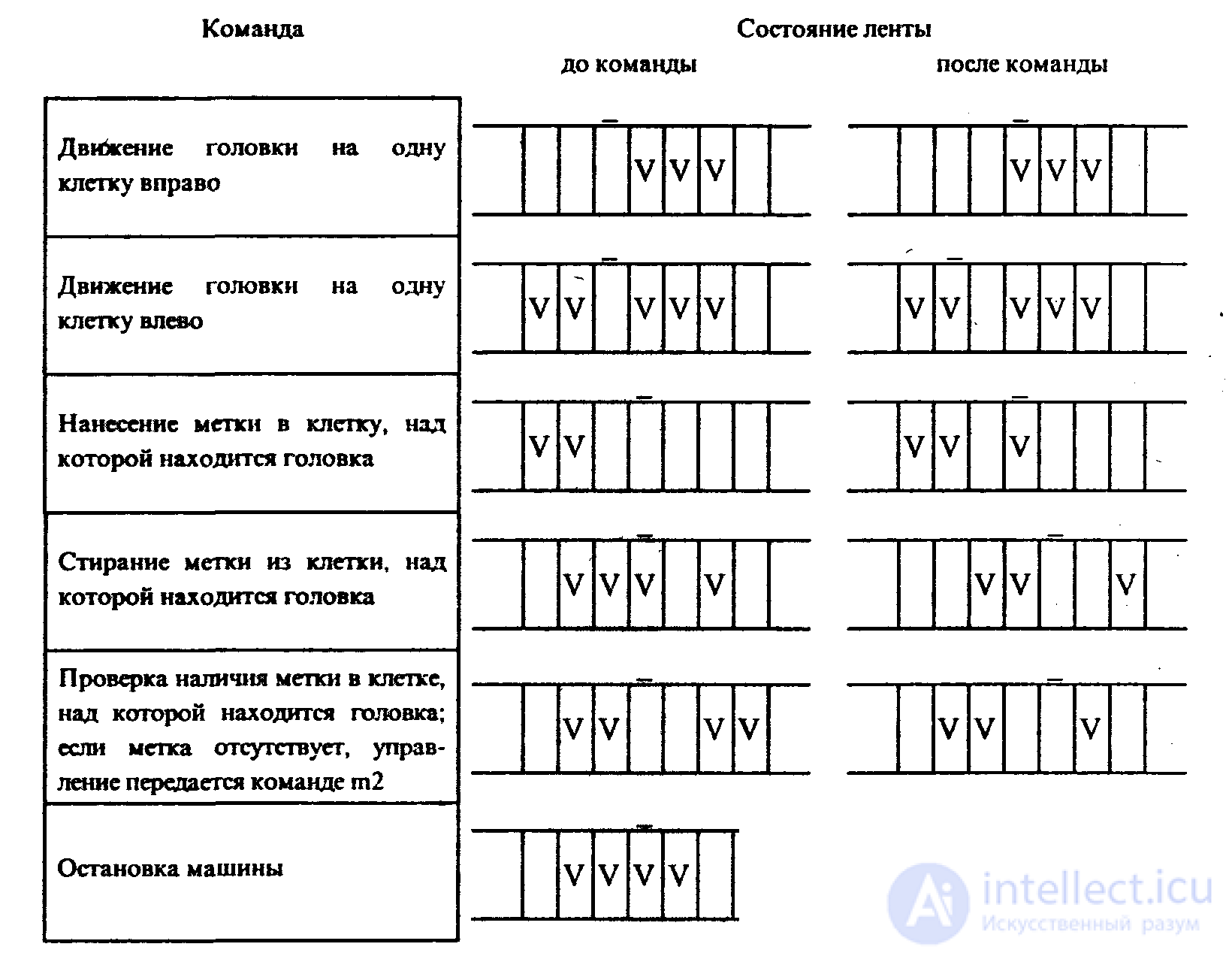
Рис.1.1. Команды машины Поста.

Ситуации, в которых головка должна наносить метку там, где она уже имеется, или, наоборот, стирать метку там, где ее нет, являются аварийными (недопустимыми).

Программой для машины Поста будем называть непустой список команд, такой что 1) на п-м месте команда с номером n; 2) номер т каждой команды совпадает с номером какой-либо команды списка.

С точки зрения свойств алгоритмов, изучаемых с помощью машины Поста, наибольший интерес представляют причины останова машины при выполнении программы:

1) останов по команде «стоп»; такой останов называется результативным и указывает на корректность алгоритма (программы);

2) останов при выполнении недопустимой команды; в этом случае останов называется безрезультативным;

3) машина не останавливается никогда; в этом и в предыдущем случае мы имеем дело с некорректным алгоритмом (программой).

Будем понимать под начальным состояние головки против пустой клетки левее самой левой метки на ленте. Рассмотрим реализацию некоторых типичных элементов программ машины Поста.

1. Пусть задано исходное состояние головки и требуется на пустой ленте написать две метки: одну в секцию под головкой, вторую справа от нее. Это можно сделать по следующей программе (справа от команды показан результат ее выполнения):

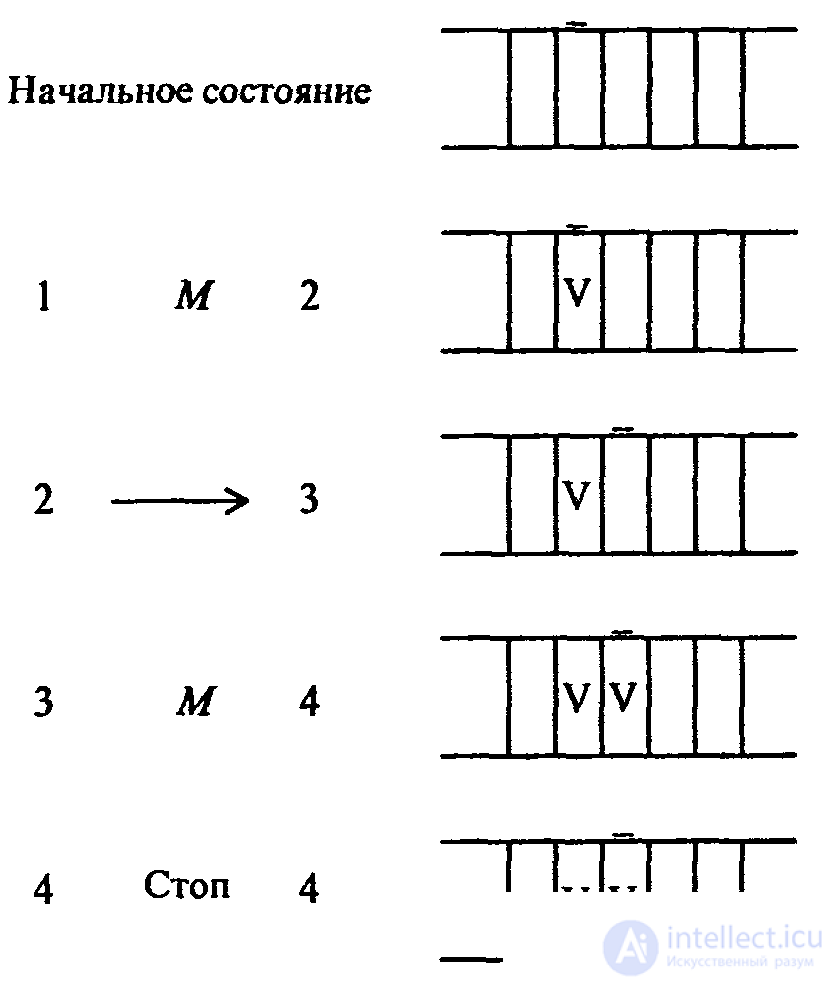
Рис.1.2. Пример элемента программы машины Поста.

2. Покажем, как можно воспользоваться командой условного перехода для организации циклического процесса. Пусть на ленте имеется запись из нескольких меток подряд и головка находится над самой крайней меткой справа. Требуется перевести головку влево до первой пустой позиции.

Программа будет иметь следующий вид:

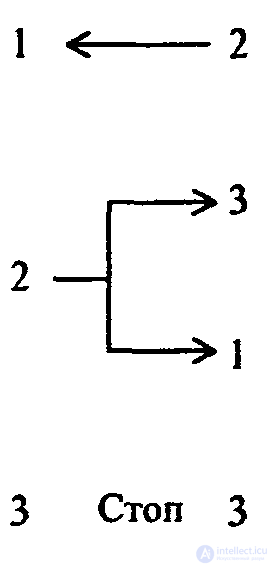
Команда условного перехода является одним из основных средств организации циклических процессов, например, для нахождения первой метки справа (или слева) от головки, расположенной над пустой клеткой; нахождение слева (или справа) от головки пустой клетки, если она расположена над меткой и т.д.

3. Остановимся на представлении чисел на ленте машины Поста и выполнении операций над ними.

Число k представляется на ленте машины Поста идущими подряд k + 1 метками (одна метка означает число «О»). Между двумя числами делается интервал как минимум из одной пустой секции на ленте. Например, запись чисел 3 и 5 на ленте машины Поста будет выглядеть так:

Обратим внимание, что используемая в машине Поста система записи чисел является непозиционной.

Составим программу для прибавления к произвольному числу единицы. Предположим, что на ленте записано только одно число и головка находится над одной из клеток, в которой находится метка, принадлежащая этому числу:

Для решения задачи можно переместить головку влево (или вправо) до первой пустой клетки, а затем нанести метку.

Программа, добавляющая к числу метку слева, имеет вид:

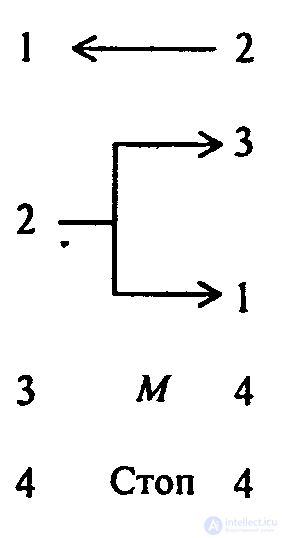
Программа, добавляющая к числу метку справа, имеет вид:

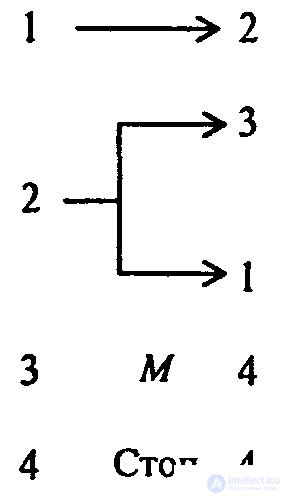
(отличие только в направлении движения головки в первой команде. Проверьте работоспособность этих программ на каких-либо частных примерах).

Предположим, что головка расположена на расстоянии нескольких клеток слева от числа, к которому нужно прибавить единицу. В этом случае программа усложняется. Появится «блок поиска числа» - две команды, приводящие головку в состояние, рассмотренное в предыдущем примере:

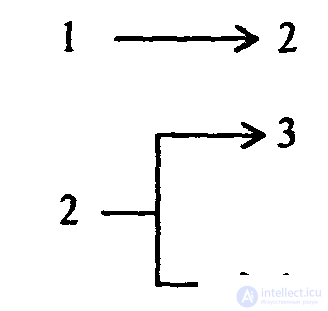
Ниже - полные тексты программ, добавляющие единицу слева и справа, соответственно:

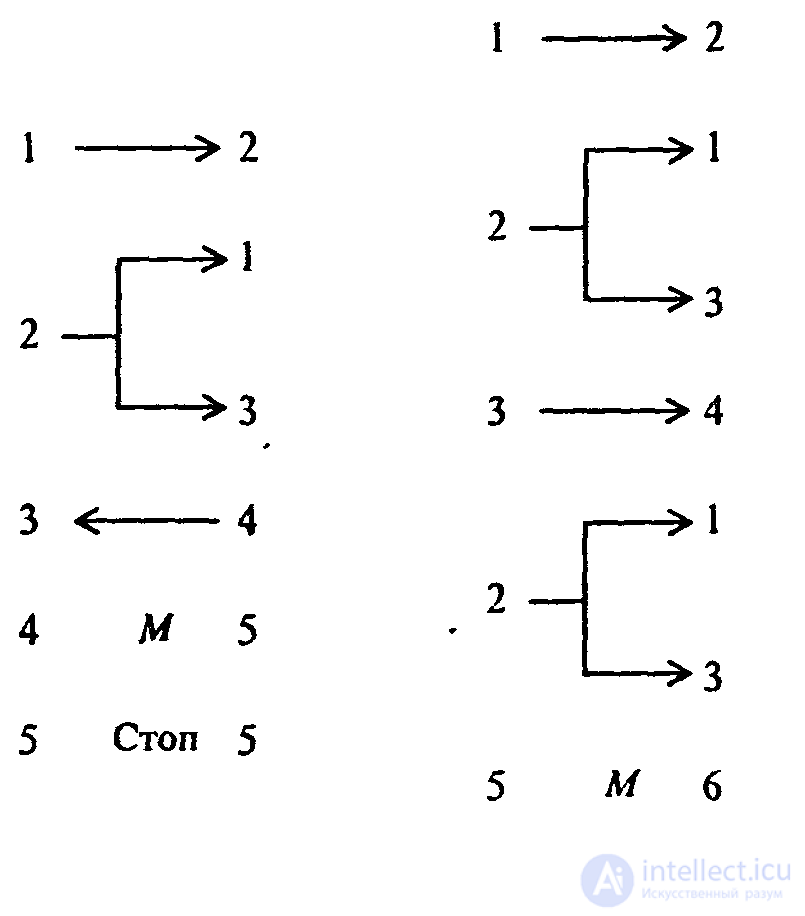
В первом случае не нужно перемещать головку к крайней левой метке числа

4. Приведем программу для сложения целых неотрицательных чисел а и и на машине Поста, когда головка находится над числом а, а число b находится правее числа а на некоторое число клеток. Эта программа реализует следующий алгоритм: первое число постепенно придвигается ко второму до их слияния, а потом стирается одна метка (иначе результат оказался бы на единицу больше правильного).

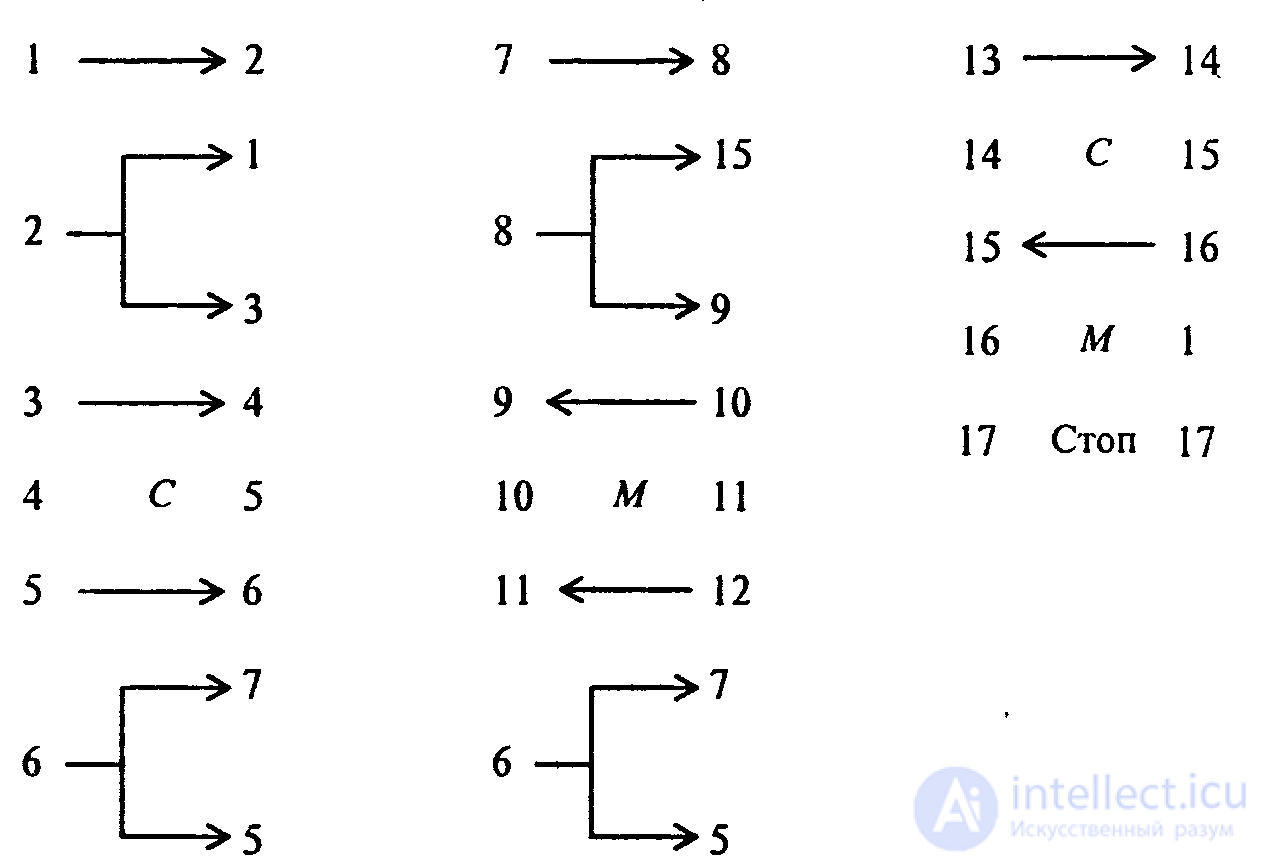
В случае более сложных начальных условий, когда неизвестно, справа или слева от головки (и на какое число клеток) находится число, можно применить такой принцип поиска числа: двигая головку вправо и влево и отмечая метками степень удаления головки от исходного положения, найти число, а потом уже применить известную программу сложения. При этом проверяется, находится ли головка над одной из меток числа и если да, то задача решена. Иначе проверяется, пуста ли секция справа от головки и следующая за ней; если обе пусты, то делается возврат головки на один шаг и ставится метка, а затем такая же операция выполняется слева и по отмеченной дорожке головка возвращается вправо и т.д. до тех пор, пока головка не натолкнется на число, после чего можно применить ранее рассмотренные выше программы:

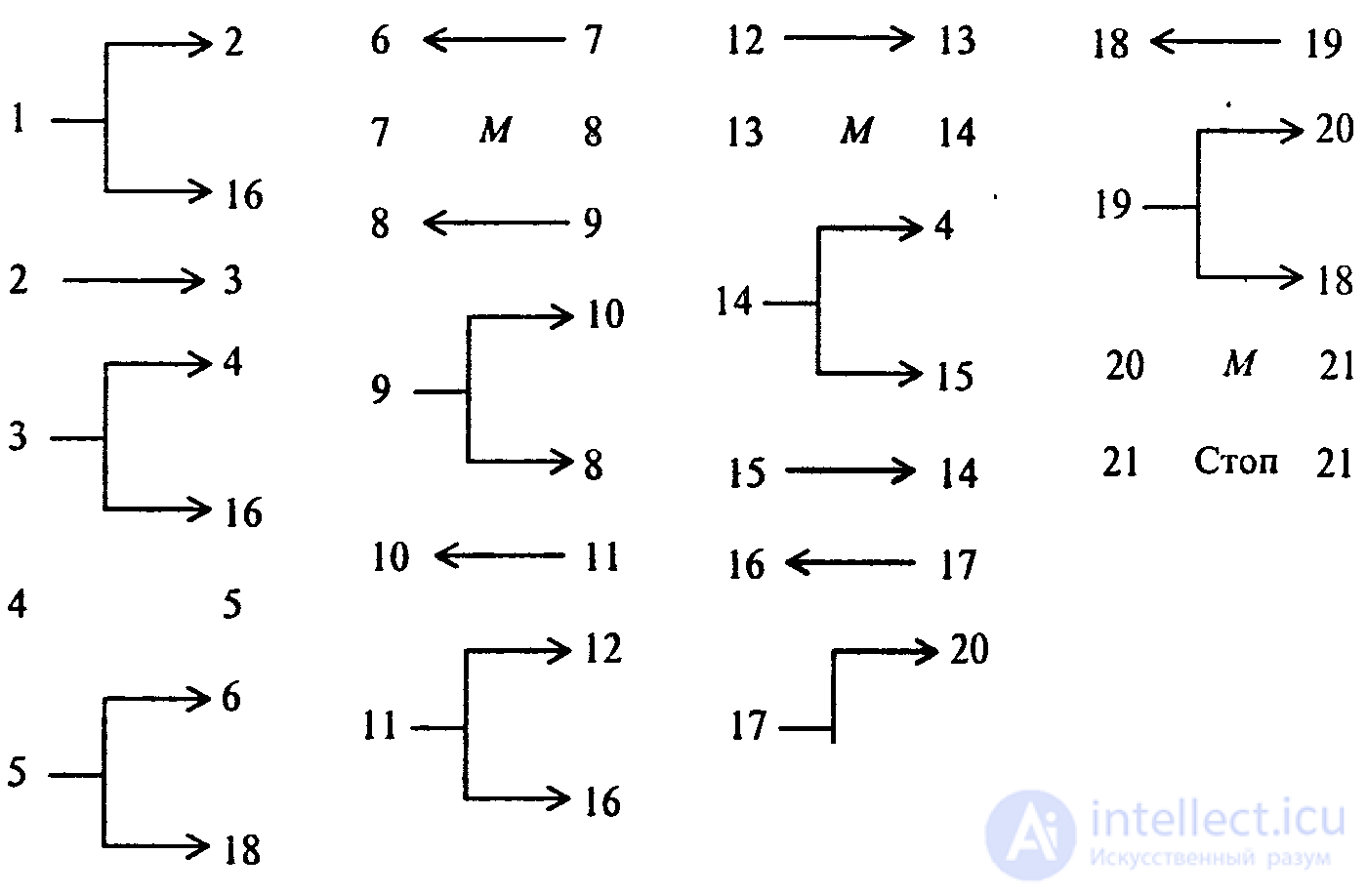
Машину Поста можно рассматривать как упрощенную модель ЭВМ. В самом деле, как ЭВМ, так и машина Поста имеют:

• неделимые носители информации (клетки - биты), которые могут быть заполненными или незаполненными;

• ограниченный набор элементарных действий - команд, каждая из которых

выполняется за один такт (шаг).

Обе машины работают на основе программы. Однако, в машине Поста информация располагается линейно и читается подряд, а в ЭВМ можно читать информацию по адресу; набор команд ЭВМ значительно шире и выразительнее, чем команды машины Поста и т.д.

Пример 1

На ленте в одной из ячеек поставлена ​​метка (остальные ячеек являются пустыми). Каретка стоит на некотором расстоянии левее эту ячейку. Нужно подвести каретку к ячейке, стереть метку и остановить каретку слева от этой ячейки.

Решение . Сначала попробуем описать алгоритм обычным языком. Поскольку нам известно, что каретка стоит напротив пустой ячейки, но неизвестно, сколько шагов нужно сделать к заполненной ячейки, мы можем сразу сделать шаг вправо; проверить, заполнена ячейка; если она пуста, то повторять эти действия до тех пор, пока не столкнемся с заполненную ячейку. Как только мы ее найдем, мы выполним операцию стирания, после чего нужно будет только сместить каретку влево и остановить выполнение программы. Программа поиска и стирания единой метки на ленте для машины Поста имеет следующий вид:

Пример 2

На ленте заданный массив меток. Увеличить длину массива на 2 метки. Каретка находится или слева от массива, или над одной из ячеек массива.

Решение .

1.? 2: 3 (команды 1 и 2 - передвигаем каретку к массиву)

2. → 1

3. → 4 (команды 3 и 4 - передвигаем каретку до конца массива)

4.? 5: 3

5. V 6 (команды 5-7 - ставим 2 метки в конец массива)

6. → 7

7. V 8

8.! (Стоп)

Пример 3

Задано два массива меток, которые находятся на некотором расстоянии друг от друга. Нужно объединить их в один массив. Каретка находится над крайней левой меткой первого массива (в исходном состоянии).

Вопросы:

1. Сравните машины Тьюринга и Поста.

2. Зачем нумеруются строки в программе для машины Поста?

Задачи:

1. Напишите программу для машины Поста, которая увеличивает (уменьшает) число в единичной системе счисления на единицу.

Каретка расположена слева от числа.

2. Напишите программу для машины Поста, которая складывает два числа в единичной системе счисления.

Каретка расположена над пробелом, разделяющим эти числа на ленте.

3. Что делают следующие программы для машины Поста:

Выводы из данной статьи про машина поста указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое машина поста и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория цифровых автоматов

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.