Лекция
Привет, сегодня поговорим про способы описания работы дискретных устройств, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое способы описания работы дискретных устройств , настоятельно рекомендую прочитать все из категории Теория автоматов.
Цифровую систему можно представить в виде устройства переработки информации, состоящую из двух частей: операционной и управляющей (рис.3.1).
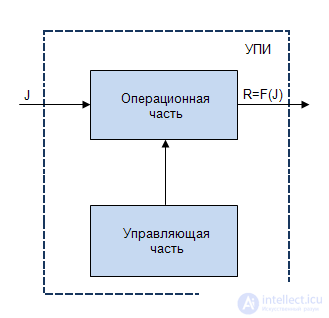
Операционная часть в этом случае представляет собой набор функциональных узлов типа счетчик, регистр, сумматор, дешифратори т.п., с соответствующими связями. На базе этих функциональных узлов выполняются все элементарные операции из множества, определяемого видом зависимости  (рис.3.1)
(рис.3.1)
В большинстве случаев это операции передачи, сдвига, запоминания чисел, анализа сопровождающих указанные операциипризнаков. На практике набор операций варьируется в зависимости от конкретных технических требований (время решения задачи, тип системы элементов), однако во всех случаях он должен быть достаточным для решения задачи.
Процесс решения заключается в упорядоченном (программном) выполнении перечисленных выше элементарных операций и для своей технической реализации требует использования специального датчика программной распределенной во времени и впространстве последовательности импульсов. Эти импульсы, воздействуя на соответствующие узлы операционной части, обеспечат упорядоченную последовательность выполнения элементарных операций (рис.3.2). Операционную часть можно назватьоперационным автоматом (ОА).

Таким образом, выделенная ранее управляющая часть устройства преобразования информации может рассматриваться как некоторый блок, обеспечивающий программное управление процессом преобразования информации, то есть как управляющийавтомат (УА). Сам же принцип программного управления сводится к упорядоченной (программной) выработке сигналов-команд, выполнение которых приводит к достижению заданной цели.
Основным элементом программного управления на рассматриваемом уровне является микрокоманда.
 -множество микрокоманд
-множество микрокоманд  микропрограммных автоматов как составной частиустройств управления.
микропрограммных автоматов как составной частиустройств управления.
Микрокомандой в дальнейшем будем называть управляющий сигнал (потенциал, импульс), осуществляющий выполнение одного элементарного шага в процессе решения задачи (рис.3.3).
Микрооперация - наименование микрокоманды.
Микрокоманде, представленной на рис.3.3, соответствует микрооперация: "Передать число из Рг I в Рг2".
В каждом процессе управления можно выделить некоторое множество различных микроопераций, которое называется набороммикроопераций.
 -микрокоманда, состоящая из микроопераций (МО)
-микрокоманда, состоящая из микроопераций (МО)
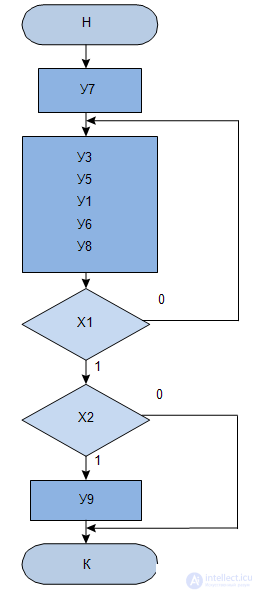
Микропрограмма представляет собой упорядоченную последовательность микроопераций заданного набора. Это определениеявляется частным, т.к. охватывает только те случаи управления, когда последовательность управляющих сигналов не меняется в зависимости от некоторых признаков, сопровождающих процесс обработки информации. В общем же случае последовательностьмикроопераций может меняться в зависимости от признаков, сопровождающих процесс обработки информации. Поэтому в составмикропрограммы кроме микроопераций, вводят также условия, в зависимости от выполнения или невыполнения которых изменяется последовательность микроопераций. По признаку отсутствия или наличия условий, в зависимости от которых меняется последовательность микроопераций, все микропрограммы делятся на две группы: не разветвляющиеся и разветвляющиеся. Разветвляющиеся микропрограммы делятся, в свою очередь, на две группы: микропрограммы без циклов и микропрограммы с циклами. В общем случае микропрограммы могут содержать в качестве своих частей все три вида: не разветвляющиеся части, разветвляющиеся и циклические.
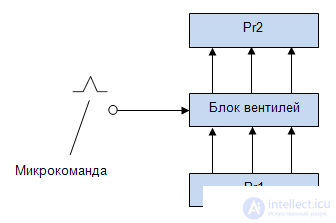
Например, на рис.3.4) показана МП операции сложения. Если ввести формальное переобозначение микрокоманд ( 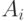 или
или 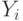 ), то для МП на рис.3.4,б получим ГСА ГСА МП показанную на рис.3.5.
), то для МП на рис.3.4,б получим ГСА ГСА МП показанную на рис.3.5.
Последовательность выполнения МК определяется функциями перехода
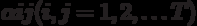 от множества логических переменных
от множества логических переменных  . Функции переходаобладают 2 свойствами: полноты и ортогональности.
. Функции переходаобладают 2 свойствами: полноты и ортогональности.

T

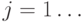
Свойство ортогональности говорит об однозначности перехода, а свойство полноты о том, что этот переход обязательно существует.
Способы формальной записи МП, удовлетворяющие перечисленным выше свойствам, это:
ГСА находят широкое применение в практике проектирования устройств ЦВМ и, в частности, микропрограммных автоматов в силу их хорошей обозримости, простоты конструкции языка и возможности преобразований и формального перехода к автоматному отображению.
Основными символами, используемыми при записи граф-схем алгоритмов (ГСА), будем считать:
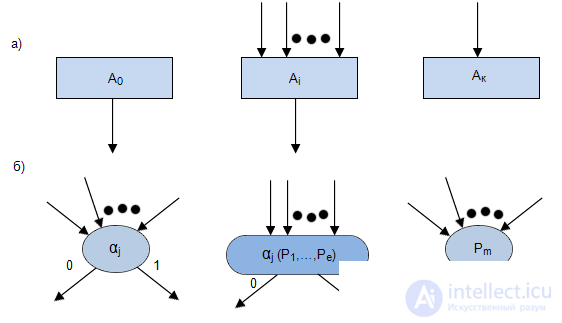
Из всего множества операторов выделяются:
 ,
, ,
, .
.Начальный оператор в дальнейшем (если это особо не оговаривается) будем рассматривать как оператор, символизирующий начало работы алгоритма.
Особенность записи оператора 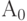 в ГСА состоит в том, что в этот оператор не входит ни одной стрелки.
в ГСА состоит в том, что в этот оператор не входит ни одной стрелки.
Конечный оператор будем рассматривать как оператор, символизирующий конец работы алгоритма.
Особенность записи оператора и 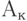 в ГСА состоит в том, что из этого оператора не выходит ни одной стрелки.
в ГСА состоит в том, что из этого оператора не выходит ни одной стрелки.
Произвольные операторы будем рассматривать как символы, обозначающие определенные действия, акты, связанные с реализацией алгоритма.
Особенность записи операторов  состоит в том, что в эти операторы могут входить несколько стрелок, но выходит всегда только одна стрелка.
состоит в том, что в эти операторы могут входить несколько стрелок, но выходит всегда только одна стрелка.
Под логическим условием будем понимать логическую функцию вида  , где
, где  элементарные логические условия. Особенность записи логических условий состоит в том, что они могут иметь несколько входящих стрелок и только две выходящие, помеченные символами "О" и "I" в со-ответствии со значением логического условия. В дальнейшем будем допускать также ГСА замену левой части выражения вида
элементарные логические условия. Особенность записи логических условий состоит в том, что они могут иметь несколько входящих стрелок и только две выходящие, помеченные символами "О" и "I" в со-ответствии со значением логического условия. В дальнейшем будем допускать также ГСА замену левой части выражения вида  его правой частью.
его правой частью.
Стрелки обеспечивают упорядочение последовательности выполнения операторов и проверки логических условий, а также их взаимосвязей.
Выполнение алгоритма всегда начинается с оператора 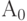 и заканчивается оператором
и заканчивается оператором 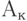 .
.
В общем виде для каждой операторной вершины формула перехода записывается так:

причем свойства ортогональности и полноты так же соблюдаются. Кроме того считается, что значения наборов логических условий в процессе выполнения операторов не меняются.
Для МП, представленной на рис.3.7, формулы перехода будут записаны так:
 ;
;
 ;
;
 ;
;
 ;
;

Говорят, что задана матричная схема алгоритма (МСА), если задана матрица вида

где 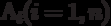 -операторы,
-операторы,
 - начальный и конечный операторы,
- начальный и конечный операторы,
 - логические условия, имеющие тот же смысл, что и в ГСА.
- логические условия, имеющие тот же смысл, что и в ГСА.
| А1 | А2 | А3 | Аk | |
|---|---|---|---|---|
| A0 | 1 | |||
| A1 | p1 | p1 | ||
| A2 | 1 | |||
| A3 | p2 | p2 |
В MCA 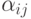 принято рассматривать как такую логическую функцию, что если выполнялся оператор
принято рассматривать как такую логическую функцию, что если выполнялся оператор 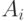 и на образовавшемся наборе
и на образовавшемся наборе  значений элементарных логических условий функция
значений элементарных логических условий функция 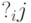 получила значение, равное единице, то непосредственно после оператора
получила значение, равное единице, то непосредственно после оператора 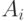 должен выполняться оператор
должен выполняться оператор 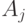 .
.
В рис.3.1,а приводится МСА МП, показанной на рис.3.7.
Основное достоинство рассматриваемых ниже логических схем алгоритмов (ЛСА) состоит в том, что, являясь по существу разновидностью языка операторных схем, они допускают запись алгоритма в строчку, что часто является удобным, т.к. появляется возможность исключить процесс рисования, вычерчивания, как это имеет место в ГСА. Важным является также наличие развитой системы преобразований ЛСА и возможности формального перехода к автоматному отображению.
Основными элементами ЛСА являются так же, как и в ГСА, операторы и логические условия.
Основные отличия от ГСА состоят в том, что для указания взаимосвязей между операторами и логическими условиями используются верхние и нижние стрелки.
Логической схемой алгоритма называется строчка, составленная из символов операторов  , или
, или  и логических условий
и логических условий  , а также верхних и нижних стрелок. Иногда верхние и нижние стрелки заменяют на правые и левые полускобки.
, а также верхних и нижних стрелок. Иногда верхние и нижние стрелки заменяют на правые и левые полускобки.
Итак, ЛСА- строчка, составленная из символов операторов  , логических условий
, логических условий 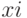 и верхних
и верхних 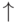 и нижних
и нижних стрелок, причем:
стрелок, причем:
 и одна конечная
и одна конечная  ;
;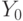 и заканчивается
и заканчивается  ;
; с одинаковыми номерами;
с одинаковыми номерами; должна быть по крайней мере одна верхняя;
должна быть по крайней мере одна верхняя;Переход по логическому условию 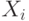 , стоящему в ЛСА
, стоящему в ЛСА

осуществляется так:
 , то после
, то после  выполнится
выполнится 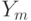 ,
, , то после
, то после  выполнится
выполнится 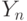 .
.Безусловный переход для ясности может быть обозначен дополнительным символом, например 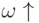 .
.
ЛСА для МП, представленной на рис. 3.7 выглядит так:

Правило чтения ЛСА состоит в следующем.
Вначале анализируется элемент ЛСА, следующий непосредственно за оператором 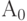 . Если рассматриваемым элементом является оператор, то он отмечается (выписывается) и на следующем шаге анализируется стоящий справа элемент (оператор или логическое условие).
. Если рассматриваемым элементом является оператор, то он отмечается (выписывается) и на следующем шаге анализируется стоящий справа элемент (оператор или логическое условие).
Если рассматриваемым элементом является логическое условие  производится проверка этого условия;
производится проверка этого условия;
Анализ ЛСА при соблюдении сформулированных правил приводит через некоторое количество шагов к получению строчки операторов, называемой значением ЛСА при заданной последовательности наборов логических условий.
Пусть задана ЛСА.

Построим соответствующую ей ГСА. За начальным оператором 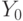 следует оператор
следует оператор  и далее логическое условие
и далее логическое условие 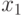 . Если логическое условие выполняется, то есть
. Если логическое условие выполняется, то есть 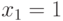 , то следующим оператором выполняется
, то следующим оператором выполняется  . Если логическое условие не выполняется, то есть
. Если логическое условие не выполняется, то есть  , то следующим оператором выполняется
, то следующим оператором выполняется 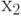 , то есть оператор, стоящий за нижней стрелкой с номером 1.
, то есть оператор, стоящий за нижней стрелкой с номером 1.
Далее в ЛСА за оператором  стоит оператор
стоит оператор 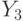 и
и  . В такой последовательности и изображаем их на ГСА. Далее строим аналогичным образом.
. В такой последовательности и изображаем их на ГСА. Далее строим аналогичным образом.
Одной важной особенностью ЛСА является возможность неоднозначной записи одного и того же алгоритма.
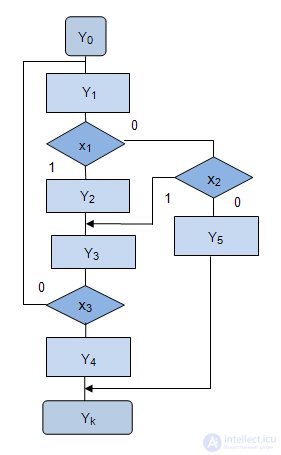
Так, ГСА на рис.3.8 может быть описана еще несколькими вариантами ЛСА:


Надеюсь, эта статья про способы описания работы дискретных устройств, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое способы описания работы дискретных устройств и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория автоматов
Комментарии
Оставить комментарий
Теория цифровых автоматов
Термины: Теория цифровых автоматов