Нормальный алгоритм - алгоритм Маркова (НАМ, также марковский алгоритм)

Привет, Вы узнаете о том , что такое нормальный алгоритм - алгоритм маркова нам также марковский алгоритм , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое нормальный алгоритм - алгоритм маркова нам также марковский алгоритм , настоятельно рекомендую прочитать все из категории Теория автоматов.

Норма́льный алгори́тм (алгори́фм) Ма́ркова (НАМ, также марковский алгоритм) — один из стандартных способов формального определения понятия алгоритма(другой известный способ — машина Тьюринга). Понятие нормального алгоритма введено А. А. Марковым (младшим) в конце 1940-х годов в работах по неразрешимости некоторых проблем теории ассоциативных вычислений. Традиционное написание и произношение слова «алгорифм» в этом термине также восходит к его автору, многие годы читавшему курс математической логики на механико-математическом факультете МГУ.

Нормальный алгоритм описывает метод переписывания строк, похожий по способу задания на формальные грамматики. НАМ является Тьюринг-полным языком, что делает его по выразительной силе эквивалентным машине Тьюринга и, следовательно, современным языкам программирования. На основе НАМ был созданфункциональный язык программирования Рефал.

 

 

Описание 

Нормальные алгоритмы являются вербальными, то есть предназначенными для применения к словам в различных алфавитах.

Определение всякого нормального алгоритма состоит из двух частей: определения алфавита алгоритма (к словам из символов которого алгорифм будет применяться) и определения его схемы. Схемой нормального алгоритма называется конечный упорядоченный набор так называемых формул подстановки, каждая из которых может быть  простой  или заключительной. 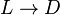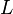Простыми формулами подстановки называются слова вида , где  и 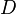 — два произвольных слова в алфавите алгоритма (называемые, соответственно, левой и правой частями формулы подстановки). 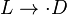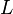Аналогично, заключительными формулами подстановки называются слова вида , где  и 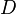 — два произвольных слова в алфавите алгоритма. Об этом говорит сайт https://intellect.icu . При этом предполагается, что вспомогательные буквы  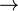и 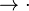 не принадлежат алфавиту алгоритма (в противном случае на исполняемую ими роль разделителя левой и правой частей следует избрать другие две буквы).

Примером схемы нормального алгоритма в пятибуквенном алфавите 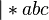 может служить схема

Процесс применения нормального алгоритма к произвольному слову 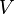 в алфавите этого алгоритма представляет собой дискретную последовательность элементарных шагов, состоящих в следующем. Пусть  — слово, полученное на предыдущем шаге работы алгорифма (или исходное слово 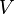, если текущий шаг является первым). Если среди формул подстановки нет такой, левая часть которой входила бы в 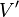, то работа алгорифма считается завершенной, и результатом этой работы считается слово 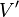. Иначе среди формул подстановки, левая часть которых входит в 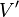, выбирается самая первая. Если эта формула подстановки имеет вид 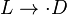, то из всех возможных представлений слова  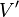в виде  выбирается такое, при котором 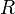 — самое короткое, после чего работа алгорифма считается завершенной с результатом 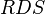. Если же эта формула подстановки имеет вид 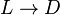, то из всех возможных представлений слова  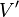в виде  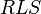выбирается такое, при котором  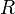— самое короткое, после чего слово  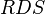 считается результатом текущего шага, подлежащим дальнейшей переработке на следующем шаге.

Например, в ходе процесса применения алгорифма с указанной выше схемой к слову 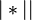 последовательно возникают слова 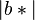, , 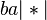, , 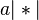, , 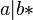, , 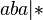,  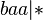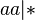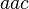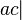и 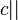, после чего алгорифм завершает работу с результатом 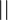. Другие примеры смотрите ниже.

Любой нормальный алгорифм эквивалентен некоторой машине Тьюринга, и наоборот — любая машина Тьюринга эквивалентна некоторому нормальному алгорифму. Вариант тезиса Черча — Тьюринга, сформулированный применительно к нормальным алгорифмам, принято называть «принципом нормализации».

Нормальные алгорифмы оказались удобным средством для построения многих разделов конструктивной математики. Кроме того, заложенные в определении нормального алгорифма идеи используются в ряде ориентированных на обработку символьной информации языков программирования — например, в языке Рефал.

Примеры 

Пример 1 

Использование алгоритма Маркова для преобразований над строками.

Алфавит:

{ а...я, А...Я, "пробел", " точка " }

Правила:

1. А → апельсин
2. кг → килограмм
3. М → магазинчике
4. Т → том
5. магазинчике → ларьке ( заключительная формула)
6. в том ларьке → на том рынке

Исходная строка:

Я купил кг Аов в Т М.

При выполнении алгоритма строка претерпевает следующие изменения:

1. Я купил кг апельсинов в Т М.
2. Я купил килограмм апельсинов в Т М.
3. Я купил килограмм апельсинов в Т магазинчике.
4. Я купил килограмм апельсинов в том магазинчике.
5. Я купил килограмм апельсинов в том ларьке.

На этом выполнение алгоритма завершится (так как будет достигнута формула № 5, которую мы сделали заключительной).

Пример 2 

Данный алгоритм преобразует двоичные числа в «единичные» (в которых записью целого неотрицательного числа N является строка из N палочек). Например, двоичное число 101 преобразуется в 5 палочек: |||||.

Алфавит:

{ 0, 1, | }

Правила:

1. 1 → 0|
2. |0 → 0||
3. 0 → "" (пустая строка)

Исходная строка:

101

Выполнение:

1. 0|01
2. 0|00|
3. 00||0|
4. 00|0|||
5. 000|||||
6. 00|||||
7. 0|||||
8. |||||

Вау!! 😲 Ты еще не читал? Это зря! 

Прочие абстрактные исполнители и формальные системы вычислений 

• Машина Тьюринга  (автоматное программирование)
• Машина Поста  ( автоматное программирование )
• Рекурсивная функция ( теория вычислимости)
• Лямбда-исчисление ( функциональное программирование )
• Brainfuck (императивное программирование )

Языки, основанные на нормальных алгоритмах 

• РЕФАЛ
• Thue

Выводы из данной статьи про нормальный алгоритм - алгоритм маркова нам также марковский алгоритм указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое нормальный алгоритм - алгоритм маркова нам также марковский алгоритм и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория автоматов

Из статьи мы узнали кратко, но содержательно про нормальный алгоритм - алгоритм маркова нам также марковский алгоритм