Лекция
Game: Perform tasks and rest cool.8 people play!
Play gameПривет, Вы узнаете о том , что такое прикладная теория цифровых автоматов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое прикладная теория цифровых автоматов, птца , настоятельно рекомендую прочитать все из категории Теория цифровых автоматов.
В теме рассмотрены основы анализа и синтеза простых и конечных автоматов имеющих память.
Даны формы представления автоматов в разных базисах с помощью переключательных функций, их инимизация, с использованием метода Квайна, импликантной матрицы, диаграммы Вейча и т.д.
Дана методика построения логических схем.
Уделяется внимание конечным автоматам, имеющим память, различным формам их представления, методике построения кодированных таблиц и структурному синтезу.
Переключательные функции и их основные свойства.
2. Минимизация переключательных функций.
3. Анализ и синтез комбинационных схем.
4. Анализ и синтез конечных автоматов с памятью.
Game: Perform tasks and rest cool.8 people play!
Play game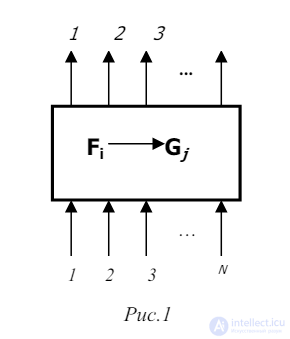
Game: Perform tasks and rest cool.8 people play!
Play game
Устройство, работа которого описывается вышеприведенной таблицей, является конечным автоматом без памяти или комбинационной схемой.
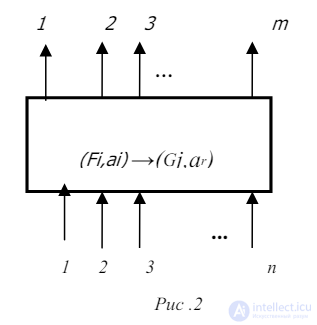
Кроме указанных выше устройств, которые с функциональной точки зрения представляют собой простые устройства, существуют более сложные устройства, на в – новое состояние автомата. нированные конечные автоматы с слову однозначно соответствует вы том. Это вызвано прежде всего тем, что в компьютерах, в ос е импульса и т.д. При оп а. Допустим, им Каждому вие десятичную цифру от 0 до 3. Вышеприведенная таблица примет вид: ыходах которых информация определяется не только входной информацией, но и тем состоянием, в котором находилось это устройство. Таким преобразователем является конечный автомат с памятью. Состояние такого автомата определяется состоянием памяти. Для определения состояния автомата введем конечный алфавит A=(a0 ,a1 ,….aq). Символ ai отражает внутреннее состояние автомата. Пара Fi , ai полностью определяет выходное слово и новое состояние автомата, в которое он перейдет после подачи на входы Fi слова. Правило работы такого автомата можно представить с помощью таблицы: (Fi,at) → (Gj ,ar), где Gj – выходное слово, ar Структура рассмотренного автомата дается на рис.2
настоящем курс матриваются детерми памятью и без памяти, в которых каждому входному е расс ходной сигнал. В компьютерах входная и выходная информация кодирована двухбуквенным двоичным алфави новном, используются двоичная система счисления или системы счисления с другим основанием с двоичным кодированием символов. Кроме этого, в компьютере для хранения информации используются двухпозиционные элементы, для которых двоичное кодирование состояния является естественным. Физическим аналогом двоичного алфавита в схемах компьютера могут быть высокий или низкий потенциал, наличие или отсутстви ределении функционирования схемы эти величины можно выразить любой парой символов. Обыкновенно такими символами являются 1 и 0. В соответствии с этим функционирование любой схемы компьютера определяется следующим образом: на вход схемы подается некоторая совокупность нулей и единиц, которая вызывает на выходе схемы появление определенной совокупности нулей и единиц. Рассмотрим пример такого кодирования . Допустим, что X=(x1,x2 ,x3) алфавит содержит три символа, Y=(y1 ,y2 ,y3 ,y4 ) алфавит – четыре символ еем конечный автомат без памяти, который преобразует слово, состоящее из двух символов, с алфавита X в слово из одного символа алфавита Y. Представим правило функционирования автомата с помощью следующей таблицы:

Каждому вие десятичную цифру от 0 до 3. Вышеприведенная таблица примет вид:
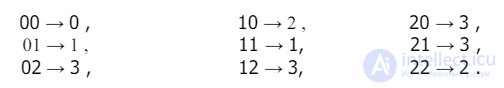
настоящем курсе рас риваются воп ы, связанные с анали нечных автоматов. С остых схем или элементов, при которых собранная схема осуществляет заданное правило пре Методы синтеза схем компьютера в современной литературе развиваются в основном на основании математической логики и теории дискретных автоматов. Для решения задачи синтеза, прежд основании которых должна быть построена схема преобразователя. Один и тот же закон преобразования информации может быть осуществлен с помощью различных схем. Для оценки технической реализации вводятся критерии: сложность схемы, ее быстродействие и надежность. Методы ределяются на основании выбранных критериев, так как в одном случае для оценки схемы преимущество может отдаваться быстродействию, в других случаях – ее сложности или надежности. Задача анализа схем заключается в представлении их в аналитическом виде, с целью их оценки или дальнейшего преобразования.
Исследование, описанное в статье про прикладная теория цифровых автоматов, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое прикладная теория цифровых автоматов, птца и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория цифровых автоматов
Из статьи мы узнали кратко, но содержательно про прикладная теория цифровых автоматов
Комментарии
Оставить комментарий
Теория цифровых автоматов
Термины: Теория цифровых автоматов