Лекция
Диаграммы Венна и диаграммы Эйлера — это графические способы представления множеств и их взаимосвязей, но они имеют различия в построении и интерпретации.
Диаграммы Венна и Эйлера выглядят очень похожими, поэтому понятно, что многим людям сложно понять разницу. Хотя оба типа диаграмм основаны на теории множеств, есть некоторые тонкие различия, которые делают их уникальными. Надеемся, что эта статья прояснит ваши сомнения относительно диаграмм Венна против диаграмм Эйлера, и я приведу несколько примеров, чтобы прояснить это.
Как я упоминал ранее, оба набора диаграмм основаны на теории множеств. диаграмма венна показывает все возможные логические отношения между коллекцией множеств. Но диаграмма эйлера показывает только те отношения, которые существуют в реальном мире.
Давайте начнем с очень простого примера. Давайте рассмотрим суперсет животных с млекопитающими и птицами в качестве подмножеств. Диаграмма Венна показывает пересечение между двумя наборами, даже если такая возможность не существует в реальном мире. Диаграмма Эйлера, с другой стороны, не показывает пересечения.
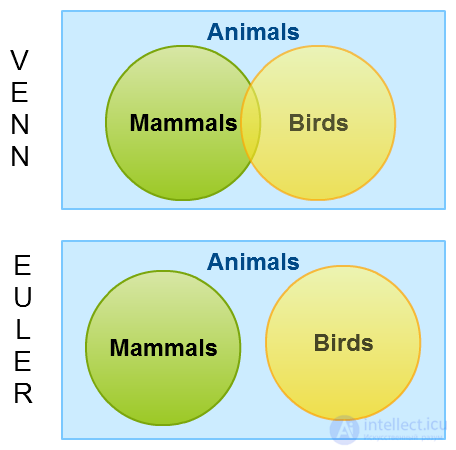
Диаграммы Венна показывают все возможные комбинации, даже если они не существуют в сценарии реального мира
Теперь давайте рассмотрим более сложный пример, включающий колоду карт. Опять же, важно иметь в виду разницу между двумя типами диаграмм, все возможные комбинации против реальных комбинаций . Давайте возьмем карты как суперсет и черные карты, красные карты и алмазы в качестве подмножеств.
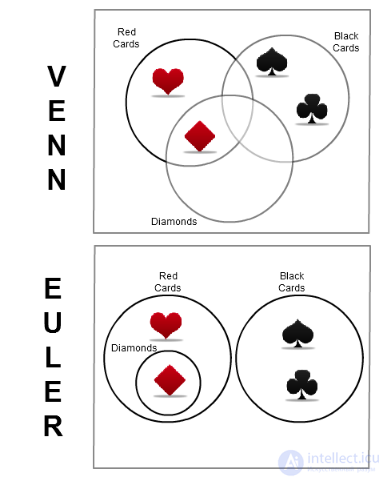
Как одни и те же данные представлены по-разному, используя диаграммы Венна и Эйлера
Как показывает приведенный выше пример, диаграммы Венна показывают четыре пересечения, которые не имеют каких-либо данных, поскольку должны показывать все возможные комбинации.
Существуют различные методы преобразования диаграмм Венна в диаграммы Эйлера и наоборот. Ознакомьтесь с этой замечательной вики-статьей о диаграммах Эйлера, в которой объясняются некоторые методы, которые можно использовать для преобразования диаграмм Венна в диаграммы Эйлера. Я надеюсь, что приведенные выше примеры помогли вам прояснить ваши сомнения относительно диаграмм Венна против диаграмм Эйлера.
Диаграммы Эйлера в отличие от диаграмм Венна изображают отношения между множествами: непересекающиеся множества изображены непересекающимися кругами, а подмножества изображены вложенными кругами.
Диаграммы Венна основаны на существенно иной идее, чем круги Эйлера. Круги Эйлера возникли на основе идей силлогистики Аристотеля. Диаграммы Венна были созданы для решения задач математической логики. Их основная идея разложения на конституенты возникла на основе алгебры логики.
На рис. ниже даны диаграммы Венна и Эйлера для 3 множеств однозначных натуральных чисел:

| Критерий | Диаграмма Венна | Диаграмма Эйлера |
|---|---|---|
| Полнота покрытия | Показывает все возможные пересечения, даже если они пустые. | Показывает только существующие пересечения. |
| Использование областей | Всегда включает все возможные зоны пересечений, даже если в них нет элементов. | Не включает пустые пересечения (если множества не пересекаются, их области не пересекаются). |
| Применение | Чаще используется в логике и теории множеств, особенно в математике. | Чаще используется в информатике, когнитивных науках и философии. |
| Визуальное представление | Более формализована и стандартизирована. | Гибкая в построении, форма областей может сильно отличаться. |
Вывод:
Диаграммы Венна подходят для строгого анализа всех возможных отношений между множествами, а диаграммы Эйлера — для более интуитивного отображения реальных связей между множествами.
Если у вас есть какие-либо вопросы, не стесняйтесь задавать их в разделе комментариев.
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.