Отображения

Привет, сегодня поговорим про отображения, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое отображения , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

Пусть даны два множества Х = {Х1, ..., хn} и Y = {У1, ..., уn}. Если каждому элементу Х Î Х поставлен в соответствие по определенному закону конкретный элемент У Î Y, то говорят, что задано Отображение множества Х во множество Y. Обозначается Х®Y.

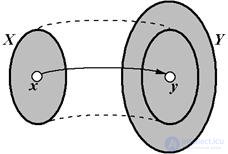
Рис. 1.8 – Отображение X®Y

При отображении Х в Y каждому элементу Х Î Х соответствует один и только один элемент У Î Y. Этот элементУ Î Y называется Образом Элемента Х Î Х, а элемент Х Î Х, в свою очередь называется Прообразом элемента У ÎY.

Итак, при отображении Х в Y каждый элемент Х Î Х имеет один и только один образ У Î Y. Однако совсем не обязательно, чтобы и всякий элемент У Î Y был образом некоторого элемента Х Î Х. Другими словами, прообразУ Î Y не обязательно принадлежит множеству Х.

· Если любой У Î Y – это образ, по крайней мере, одного Х Î Х, то говорят, что имеет место Отображение Х наY или Сюръекция, Или Накрытие. Об этом говорит сайт https://intellect.icu . В противном случае говорят, что задано Отображение Х в Y.

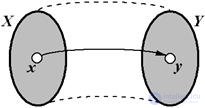
Рис. 1.9 – Отображение X на Y (сюръекция)

Если для любых двух различных элементов Х1, х2 Î Х их образы у1, у2 Î Y также различны, то говорят, что задано Взаимно-однозначное отображение Х в Y Или Инъекция.

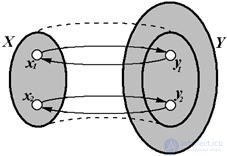
Рис. 1.10 – Взаимно-однозначное отображение Х в Y (инъекция)

Отображение, которое является од­новременно инъекцией и сюръекцией, называется Взаимно-однозначным отображением Х на Y или биекцией (наложением).

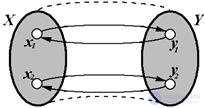
Рис. 1.11 – Взаимно-однозначное отображение Х на Y (биекция или наложение)

В общем случае при отображении А элементов Х Î Х на мно­жество элементов У Î Y А: Х ® Y элемент У Î Y может быть образом не одного, а нескольких (Х1, ..., Хn) Î Х. Совокупность элементов (всех) Х1, ..., Хn Î Х, образом которых является данный У Î Y, называется полным прообразом элемента У Î Y и обозначается А-1 (У).

Пусть Q – некоторое подмножество множества Х, на котором определено отображение А. Совокупность элементов А(Q) , являющихся образами всех элементов множества Q, называется Образом этого множества И обозначается А(Q). В свою очередь, для каждого мно­жества R из Y определяется его Полный прообраз А-1 (R) как совокупность всех тех элементов из Х, образы которых принадлежат R.

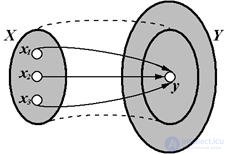
Рис. 1.12 – Общий случай отображения

Любое отображение А их Х в Y есть элемент множества Р(Х´Y), т. е. множества всех подмножеств прямого произведения Х´Y. Элемен­тами этого множества являются упорядоченные пары (Х, у) где Х Î Х, а У Î Y.

Если F – взаимно-однозначное отображение, а множества Х и Y совпадают, то F: Х®Х называетсяОтображением множества Х на себя.

Элементы (Х, х) ÎХ´Х образуют тождественное отображение Е, причем F∙F-1 = F-1∙F = E.

Надеюсь, эта статья про отображения, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое отображения и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.