Типы конечных графов

Привет, сегодня поговорим про типы конечных графов, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое типы конечных графов , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

Если множество вершин графа конечно, то он называется конечным графом. Конечный граф G = (V, Е), содержащий р вершин и q ребер, назывзется (р, q)-гpaфoм.
Пусть V == {v1, v2, …, vp} и Е == {е1, е2, …, eq} — соответственно множества вершин и ребер (р, q)-графа. Каждое ребро ek < Е соединяет пару вершин vi, vj < V, являющихся его концами (граничными вершинами). Для ориентированного ребра (дуги). различают начальную вершину, из которой дуга исходит, и конечную вершину, в которую дуга заходит. Ребро, граничными вершинами которого является одна и та же вершина, называется петлей. Ребра с одинаковыми граничными вершинами являются параллельными и называются кратными. В общем случае граф может содержать и изолированные вершины, которые не являются концами ребер и не связаны ни между собой, ни с другими вершинами.
Число ребер, связанных с вершиной vi (петля учитывается дважды), называют степенью вершины и обозначают через (vi) или deg(vi). Так, для графа на рисунке 2.2, а (v1) == 1, (v2) = 4 и т. д. Очевидно, степень изолированной вершины равна нулю ((v4)= 0). Вершина степени единицы называется концевой или висячей вершиной ((v1) = 1). Легко показать, что в любом графе сумма степеней всех вершин равна удвоенному числу ребер, а число вершин нечетной степени всегда четно. В орграфе различают положительные +(vi) и отрицательные -(vi) степени вершин, которые равны соответственно числу исходящих из vi и заходящих в vi дуг. Например, для вершины d орграфа (см. рисунок 2.1, а) имеем +(d) = 2 и —(d) = 3. Очевидно, суммы положительных и отрицательных степеней всех вершин орграфа равны между собой и равны также числу всех дуг.
Граф без петель и кратных ребер называют простым или обыкновенным. Граф без петель, но с кратными ребрами называют мультиграфом. Наиболее общий случай графа, когда допускаются петли и кратные ребра, называют псевдографом. Об этом говорит сайт https://intellect.icu . Так, граф на рисунке 2.2, б — это мультиграф, а на рисунке 2.2, а — псевдограф. Если граф не имеет ребер , то все его вершины изолированы, и он называется пустым или нуль-графом. Простой граф, в котором любые две вершины соединены ребром, называется полным (на рисунке 2.2, б приведен пример полного графа с шестью вершинами). Если множество вершин V простого графа допускает такое разбиение на два непересекающихся подмножества V1 и V2 что не существует ребер, соединяющих вершины одного и того же подмножества, то он называется двудольным или би-графом (рисунок 2.2, в). Ориентированный граф считается простым, если он не имеет строго параллельных дуг и петель.
Граф, степени всех вершин которого одинаковы и равны r, называется однородным (регулярным) r-й степени. Полный граф с n вершинами всегда однородный степени n2 — 1, а пустой граф — однородный степени 0. Граф третьей степени называют кубическим. Он обладает рядом интересных свойств и, в частности, всегда имеет четное число вершин.

 

Если граф не имеет ребер (т.е. 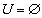), то все его вершины изолированы, и он называетсяпустым или нуль-графом.

  Простой неориентированный граф, в котором любые две вершины соединены ребром, называется полным. Полный граф с  n вершинами обозначают символом Kn (рис.4.2, граф K4 ). Граф порядка n без ребер называется пустым и обозначается On.

Граф  называется  тривиальным. Можно расширить полный граф до полного графа с петлями, добавляя петлю в каждой вершине (рис.4.6).

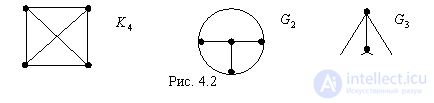
В ориентированном полном графе имеются пары ребер, по одному в каждом направлении, соединяющие любые две различные вершины.

Турниром называется орграф, любую пару вершин которого соединяет только одна дуга. Турнир отличается от полного ориентированного графа тем, что у него нет противоположно направленных дуг.

            Граф называется однородным (регулярным) степени k, если степени всех его вершин одинаковые и равны k . Однородный граф степени 1 называется паросочетанием. Примерами однородных графов могут служить графы, образованные вершинами и ребрами пяти первых правильных многогранников (или, так их называют, платоновых тел): тетраэдра и куба (степени 3), октаэдра (степени 4), додекаэдра (степени 3), икосаэдра (степени 5). Граф третьей степени называют кубическим, он обладает рядом интересных свойств и, в частности, всегда имеет четное число вершин. Три кубических графа изображены на рис.4.2.

            Из выписанной выше формулы, связывающей число звеньев графа m  со степенями его вершин, для случая однородного графа степени k (все 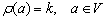 ), получим:

.

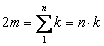Напоминаем, что 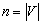 -  число вершин графа. Поэтому, если  нечетное число, то  n должно быть четным, и, следовательно, у любого однородного графа нечетной степени (и кубического тоже) всегда четное количество вершин.

            Орграф называется однородным степени k , если полустепени всех его вершин одинаковые и равны : ==. В этом случае

.

Здесь, как и раньше,  n и m - число вершин и дуг графа.

            Если множество вершин простого графа можно разбить на два непересекающихся подмножества (доли) V1 , V2 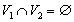 () и при этом не существует ребер, соединяющих вершины одного и того же подмножества, то такой граф называется двудольным (иначе -биграфом). Полный двудольный (у него каждая вершина из V1  соединена с каждой вершиной из V2 ). обозначают символом  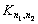где 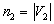 , 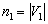. Граф  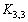 изображен на рис 4.13.

Надеюсь, эта статья про типы конечных графов, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое типы конечных графов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.

Из статьи мы узнали кратко, но содержательно про типы конечных графов