Комбинаторные объекты

Лекция 11 мин.

Привет, Вы узнаете о том , что такое комбинаторные объекты , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое комбинаторные объекты , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

Определение:

комбинаторные объекты (англ. combinatorial objects) — конечные множества, на элементы которых могут накладываться определенные ограничения, такие как: различимость или неразличимость элементов, возможность повторения одинаковых элементов и т. п.

Определение:

Если два комбинаторных объекта, различающихся только порядком элементов, считаются различными, то они называются упорядоченными (англ. ordered).

Комбинаторные объекты - это объекты или структуры, которые изучаются в комбинаторике, разделе математики, занимающемся подсчетом, анализом и исследованием комбинаторных структур и их свойств. Комбинаторика занимается перечислением, классификацией и анализом комбинаций, перестановок, размещений, разбиений и других комбинаторных объектов.

Некоторые из часто изучаемых комбинаторных объектов включают в себя:

Подмножества: Комбинаторика занимается подсчетом количества подмножеств в данном множестве и изучением их свойств.
Перестановки: Это упорядоченные последовательности элементов. Изучение различных способов упорядочивания элементов влияет на комбинаторные задачи.
Сочетания: Это неупорядоченные наборы элементов из множества. Сочетания изучают, сколькими способами можно выбрать k элементов из n, не учитывая порядок.
Разбиения: Это способы разделения множества элементов на непересекающиеся подмножества.
Графы: Комбинаторные графы, такие как деревья, графы Кэли и др., играют важную роль в комбинаторике.
Бинарные последовательности: Изучение бинарных строк и их свойств, таких как графы Хэмминга и коды исправления ошибок.
Целочисленные разбиения: Изучение способов представления целых чисел суммами целых чисел, например, разложение числа на сумму простых чисел (теория чисел).
Генерирующие функции: Инструмент, используемый в комбинаторике для анализа комбинаторных последовательностей и объектов.

Изучение комбинаторных объектов имеет множество приложений в различных областях, включая теорию чисел, теорию графов, криптографию, статистику и многие другие области математики и науки.

Примеры комбинаторных объектов

Битовые векторы

Определение:

Битовые векторы (англ. bit vectors) — последовательность нулей и единиц заданной длины.

Перестановки

Определение:

Перестановки (англ. permutations) — упорядоченный набор чисел 1,2,…,n, обычно трактуемый как биекция на множестве {1,2,…,n}, которая числу i ставит соответствие i-й элемент из набора.

Примером перестановки может служить задача о рассадке n человек за стол по n местам.

Перестановки с повторениями

Определение:

Перестановки с повторениями (англ. permutations with repetitions) — те же перестановки, однако некоторые элементы могут встречаться несколько раз.

В пример можно привести следующую задачу: имеется набор книг {a1,a2,…,an}, каждая из которых имеется в k1,k2,…,kn экземплярах соответственно. Сколько существует способов переставить книги на полке?

Размещения

Определение:

Размещение (англ. arrangement) из n по k — упорядоченный набор из k различных элементов некоторого n-элементного множества.

Примером размещения может служить задача о рассадке k человек за стол по n местам, где n>k.

Размещения с повторениями

Определение:

Размещение с повторениями (англ. arrangement with repetitions), составленное из данных n элементов по k — отображение множества k первых натуральных чисел 1,2,…,k в данное множество {a1,a2,…,an}.

В пример можно привести следующую задачу: имеется n книг, каждая в k экземплярах. Сколькими способами может быть сделан выбор книг из числа данных?

Сочетания

Определение:

Сочетания (англ. combinations) из n по k — набор k элементов, выбранных из данных n элементов.

Примером сочетания может служить задача о выборе k книг из n вариантов.

Сочетания с повторениями

Определение:

Сочетания с повторениями (англ. Об этом говорит сайт https://intellect.icu . combinations with repetitions) — те же сочетания, только теперь даны n типов элементов, из которых нужно выбрать k элементов, причем элементов каждого типа неограниченное количество, и элементы одного типа должны стоять подряд друг за другом.

В пример можно привести следующую задачу: имеется n пирожных. Сколько способов купить k пирожных?

Разбиение на неупорядоченные слагаемые

Определение:

Разбиение числа на неупорядоченные слагаемые (англ. partition) — представление числа n в виде суммы слагаемых.

Разбиение на подмножества

Определение:

Разбиение множества X на подмножества (англ. partition of a set) — семейство непустых множеств {Uα},α∈A, где A — некоторое множество индексов, если:

Uα∩Uβ=∅ для любых α,β∈A, таких что α≠β;
X=⋃α∈AUα.

Число комбинаторных объектов

Тип объекта	Число объектов
Битовые векторы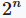
Перестановки	Pn=n!
Перестановки с повторениями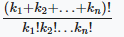
Размещения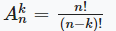
Размещения с повторениями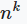
Сочетания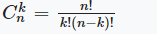
Сочетания с повторениями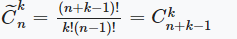
Разбиение на неупорядоченные слагаемые	Нахождение количества разбиений числа на слагаемые
Разбиение на подмножества	Числа Стирлинга второго порядка

Соответствующие доказательства

Теорема:

Число различных битовых векторов длины n равно 2ⁿ^.

Доказательство:

▹

Число битовых векторов — это частный случай размещения с повторениями 2 элементов по n. Таким образом, количество различных битовых векторов будет равно 2ⁿ.

◃

Теорема:

Число различных перестановок из n элементов равно Pn=n!

Доказательство:

▹

Перестановка — это частный случай размещения n элементов по k при k=n. Таким образом, количество различных перестановок будет равно n!

◃

Теорема:

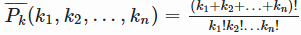Число различных перестановок с повторениями из k элементов с n группами одинаковых элементов равно Комбинаторные объекты

, где ki — это количество одинаковых элементов в i—ой группе.

Доказательство:

▹

Пусть нужно найти количество перестановок с повторениями на множестве A из k элементов. Будем учитывать, что в этом множестве n групп одинаковых элементов. Количество перестановок из k элементов, не учитывая того факта, что элементы могут быть одинаковые, будет равно k!.

В каждой итоговой перестановке у нас будет несколько раз учитываться ситуации с одинаковыми элементами ровно столько раз, сколько можно получить перестановок из ki. Таким образом количество перестановок с одинаковым первым элементом будет равно k1!, для второго элемента — k2!. Общее количество идентичных перестановок будет равно произведению данных факториалов. Итого одинаковых перестановок k1!⋅k2!⋅…⋅kn!. Ответом будем являться частное количества всех перестановок и количества одинаковых.

Получаем, что итоговое количество равно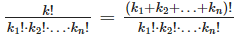 Комбинаторные объекты

◃

Теорема:

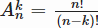Число различных размещений из n элементов по k равно Комбинаторные объекты

Доказательство:

▹

Доказательство по индукции. База k=1, тогда количество размещений из n по 1 равно n.

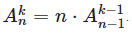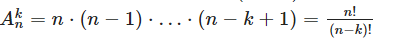При k≥2 воспользуемся правилом произведения. Выбрать первый элемент можно n различными способами. При каждом первом элементе, все что осталось образует размещение из оставшегося множества, то есть (n−1) элементов, по (k−1). Следовательно получаем рекуррентную формулу Комбинаторные объекты

. Отсюда получаем Комбинаторные объекты

◃

Теорема:

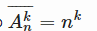Число различных размещений с повторениями из n элементов по k равно Комбинаторные объекты

Доказательство:

▹

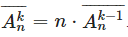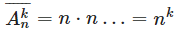Докажем по индукции. База: k=1. Тогда Комбинаторные объекты .

При k≥2 воспользуемся правилом произведения. Выбрать первый элемент можно n различными способами. При каждом первом элементе, все что осталось образует размещение с повторениями из того же самого множества, то есть из n элементов, по (k−1). Следовательно получаем рекуррентную формулу Комбинаторные объекты

. Отсюда получаем Akn¯¯¯¯¯¯=n⋅n…=nk Комбинаторные объекты

◃

Теорема:

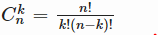Число различных сочетаний из n элементов по k равно Комбинаторные объекты

Доказательство:

▹

Всего размещений из n элементов по k равно 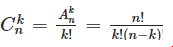Комбинаторные объекты В каждом размещении выбраны k элементов из данного множества. Если игнорировать порядок этих выбранных k элементов, мы получим некоторые сочетания из данного множества по k. Другими словами, размещение с одним и тем же набором выбранных k элементов задают одно и то же сочетание по k элементов.

Так как размещения с одним и тем же набором выбранных k элементов различаются только порядком элементов и число различных перестановок из k элементов равно k!, то итоговая формула будет равна Комбинаторные объекты

◃

Теорема:

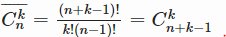Число различных сочетаний с повторениями из n элементов по k равно Комбинаторные объекты

Доказательство:

▹

Рассмотрим двоичный вектор из (n+k−1) координат, в котором (n−1) нулей и k единиц.

Будем считать нули разделителями, которые делят этот вектор на n частей.

Тогда предположим, что число единиц в i—м блоке — это число элементов ki в сочетании с повторением, которое соответствует этому вектору, где ki — это элемент из изначального множества с номером i.

Пример: Если у нас есть набор элементов 1 1 2 2 3, то k2 = 2.

Получаем, что каждому сочетанию с повторениями из n по k соответствует некоторый вектор из нулей и единиц с (n+k−1) координатами, в котором (n−1) нулей. Также наоборот, по каждому такому вектору однозначно восстанавливается сочетание с повторением, ему соответствующее. Значит, число сочетаний с повторениями из n по k совпадает с числом таких векторов.

Таких векторов столько, сколько вариантов выбрать k координат, на которых должны стоять единицы из (n+k−1). Таким образом, ответом будет являться число сочетаний из (n+k−1) по k. Тогда количество равно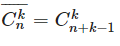 Комбинаторные объекты

◃

Вау!! 😲 Ты еще не читал? Это зря!

Генерация комбинаторных объектов в лексикографическом порядке
Получение следующего объекта
Получение номера по объекту
Получение объекта по номеру

Исследование, описанное в статье про комбинаторные объекты , подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое комбинаторные объекты и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.

Оставить комментарий

Если у вас есть какое-либо предложение, идея, благодарность или комментарий, не стесняйтесь писать. Мы очень ценим отзывы и рады услышать ваше мнение.

To reply

Comment

Для того, чтобы подтвердить, что вы не бот, ответьте:

Name

Email(not published)

Оценить