Объединение и пересечение графов

Привет, сегодня поговорим про объединение, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое объединение, пересечение графов , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

объединение графов — операция над графами, в результате которой получается граф, множества вершин и ребер которого являются объединениями множеств вершин и ребер исходных графов. Иными словами, в результирующий граф входят все ребра и вершины, которые присутствуют в исходных графах^[1].

Операцию объединения графов, как и аналогичную операцию для множеств, принято обозначать символом :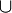

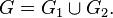
Таким образом, если

то

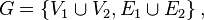
где 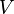 — множество вершин,  — множество ребер графа.

Пересечение графов — операция над графами, в результате которой получается граф, множества вершин и ребер которого являются пересечениями множеств вершин и ребер исходных графов. Об этом говорит сайт https://intellect.icu . Иными словами, в результирующий граф входят только те ребра и те вершины, которые присутствуют во всех исходных графах^[1].

Операцию пересечения графов, как и аналогичную операцию для множеств, принято обозначать символом :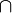

Таким образом, если

то

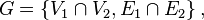
где 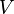 — множество вершин,  — множество ребер графа.

На этом все! Теперь вы знаете все про объединение, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое объединение, пересечение графов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.