Лекция
Сразу хочу сказать, что здесь никакой воды про теория графов, и только нужная информация. Для того чтобы лучше понимать что такое теория графов, графы, граф, способы описания графов , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
теория
граф ов — это раздел дискретной математики, изучающий свойства графов. В общем смысле граф представляется как множество вершин (узлов), соединенных ребрами. В строгом определении графом называется такая пара множеств 
, где 
есть подмножество любого счетного множества, а 
— подмножество 
.
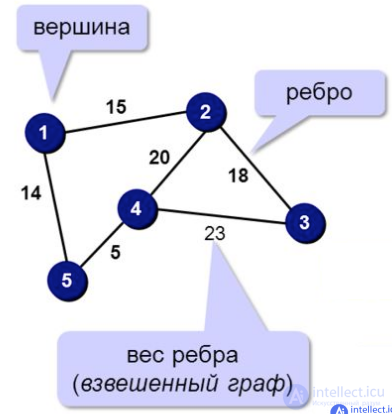
В математике , теории графов являются изучением графов, которые являются математическими структурами , используемых для моделирования попарных отношений между объектами. Граф в этом контексте состоит из вершин (также называемых узлами или точками ), которые соединены ребрами (также называемыми связями или линиями ). Различают неориентированные графы , где ребра соединяют две вершины симметрично, и ориентированные графы , где ребра связывают две вершины асимметрично; см. граф (дискретная математика)для более подробных определений и других разновидностей обычно рассматриваемых типов графов. Графы - один из основных объектов изучения дискретной математики .
Теория графов находит применение, например, в геоинформационных системах (ГИС). Существующие или вновь проектируемые дома, сооружения, кварталы и т. п. рассматриваются как вершины, а соединяющие их дороги, инженерные сети, линии электропередачи и т. п. — как ребра. Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут.
Теория графов содержит большое количество нерешенных проблем и пока не доказанных гипотез.
Родоначальником теории графов считается Леонард Эйлер. В 1736 году в одном из своих писем он формулирует и предлагает решение задачи о семи кенигсбергских мостах, ставшей впоследствии одной из классических задач теории графов. Термин «граф» впервые ввел Сильвестр, Джеймс Джозеф в 1878 году в своей статье в Nature .
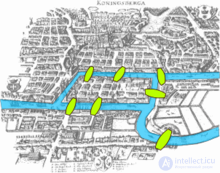
Проблема Кенигсбергского моста
Статья Леонарда Эйлера о семи мостах Кенигсберга, опубликованная в 1736 году, считается первой статьей в истории теории графов. В этой статье, а также в статье, написанной Вандермондом по проблеме рыцаря , продолжался анализ места, инициированный Лейбницем . Изучена формула Эйлера , связывающее число ребер, вершин и граней выпуклого многогранника и обобщена Коши и L'Huilier , и представляет собой начало ветви математики известной как топологии .
Спустя более чем столетие после статьи Эйлера о мостах в Кенигсберге и пока Листинг вводил понятие топологии, Кэли руководствовался интересом к определенным аналитическим формам, возникающим из дифференциального исчисления, для изучения определенного класса графов - деревьев . Это исследование имело большое значение для теоретической химии . Используемые им техники в основном касаются перечисления графов с определенными свойствами. Теория перечислительных графов возникла затем на основе результатов Кэли и фундаментальных результатов, опубликованных Полиа в период с 1935 по 1937 год. Они были обобщены Де Брейном.в 1959 году. Кэли связал свои результаты о деревьях с современными исследованиями химического состава. Слияние идей из математики с идеями из химии положило начало тому, что стало частью стандартной терминологии теории графов.
В частности, термин «граф» был введен Сильвестром в статье, опубликованной в 1878 году в журнале Nature , где он проводит аналогию между «квантовыми инвариантами» и «ко-вариантами» алгебры и молекулярных диаграмм:
«[…] Таким образом, каждый инвариант и ковариант становится выражаемым с помощью графа, в точности идентичного диаграмме Кекулеана или химикографу. […] Я даю правило геометрического умножения графов, то есть для построения графа из произведения не- или ко-варианты, чьи отдельные графы даны. […] »(курсив, как в оригинале).
Первый учебник по теории графов был написан Денесом Кенигом и опубликован в 1936 году. Другая книга Фрэнка Харари , опубликованная в 1969 году, «считалась во всем мире окончательным учебником по этому предмету» и позволили математикам, химикам, инженерам-электрикам и социологам общаться друг с другом. Харари пожертвовал все гонорары на финансирование премии Полиа .
Одной из самых известных и стимулирующих проблем в теории графов является проблема четырех цветов : «Верно ли, что любая карта, нарисованная на плоскости, может иметь области, окрашенные в четыре цвета, таким образом, что любые две области, имеющие общую границу, имеют различные цвета?" Эта проблема была впервые поставлена Фрэнсисом Гатри в 1852 году, и первое письменное упоминание о ней содержится в письме Де Моргана, адресованном Гамильтону в том же году. Было предложено много неверных доказательств, в том числе Кэли, Кемпе и др. Исследование и обобщение этой проблемы Тейтом , Хивудом , Рэмси и Хадвигеромпривело к изучению раскрасок графов, вложенных на поверхности произвольного рода . Переформулировка Тейта породила новый класс проблем - проблемы факторизации , особенно изученные Петерсеном и Кенигом . Работы Рамсея по раскраске и, в частности, результаты, полученные Тураном в 1941 году, положили начало другой ветви теории графов, экстремальной теории графов .
Проблема четырех цветов оставалась нерешенной более века. В 1969 году Генрих Хееш опубликовал метод решения проблемы с помощью компьютеров. Компьютерное доказательство, произведенное в 1976 году Кеннетом Аппелем и Вольфгангом Хакеном, фундаментально использует понятие «разрядки», разработанное Хишем. Доказательство включало проверку свойств 1936 конфигураций на компьютере и не было полностью принято в то время из-за его сложности. Более простое доказательство, учитывающее только 633 конфигурации, было дано двадцатью годами позже Робертсоном , Сеймуром , Сандерсом и Томасом
Автономное развитие топологии с 1860 по 1930 годы способствовало развитию теории графов благодаря работам Джордана , Куратовски и Уитни . Еще одним важным фактором общего развития теории графов и топологии стало использование методов современной алгебры. Первым примером такого использования является работа физика Густава Кирхгофа , который опубликовал в 1845 году свои законы Кирхгофа для расчета напряжения и тока в электрических цепях .
Введение вероятностных методов в теорию графов, особенно в исследовании Эрдеша и Реньи асимптотической вероятности связности графов, дало начало еще одной ветви, известной как теория случайных графов , которая была плодотворным источником теоретических результатов.
Терминология теории графов поныне не определена строго. В частности, в монографии Гудман, Хидетниеми, 1981 сказано: «В программистском мире нет единого мнения о том, какой из двух терминов „граф“ или „сеть“. Мы выбрали термин „сеть“, так как он, по-видимому, чаще встречается в прикладных областях». Аналогичная ситуация с терминами «вершина/точка».
Виды графов:
Определения в теории графов различаются. Ниже приведены некоторые из основных способов определения графов и связанных математических структур .
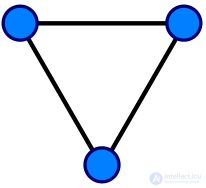
Граф с тремя вершинами и тремя ребрами.
В одном ограниченном , но очень общем смысле этого термина, граф является упорядоченная пара в составе:
, А набор из вершин (также называемые узлами или точки );
, А набор из ребер (также называемые ссылками или линией ), которые являются неупорядоченными парами вершин (то есть, ребро связанно с двумя различными вершинами).Чтобы избежать двусмысленности, этот тип объекта можно назвать именно неориентированным простым графом .
В краю 
, вершины 
и 
называются концами ребра. Говорят, что край соединяется x и и быть инцидентом на и дальше . Вершина может существовать в графе и не принадлежать ребру. Множественные ребра , недопустимые в соответствии с приведенным выше определением, - это два или более ребра, которые соединяют одни и те же две вершины.
В более общем смысле этого слова, допускающего наличие нескольких ребер, граф - это упорядоченная тройка 
в составе:
, А набор из вершин (также называемые узлами или точки );, А набор из ребер (называемая также ссылка или линия );
, функция инцидентности, отображающая каждое ребро в неупорядоченную пару вершин (то есть, ребро связано с двумя различными вершинами).Во избежание двусмысленности этот тип объекта можно назвать именно неориентированным мультиграфом .
Цикл является ребром , который соединяет вершину саму с собой. Графы, как это определено в двух определениях выше, не могут иметь циклов, потому что цикл, соединяющий вершину самому себе является ребром (для неориентированного простого графа) или инцидентно (для неориентированного мультиграфа) 
которого нет в 
. Поэтому, чтобы разрешить циклы, определения должны быть расширены. Для неориентированных простых графов определение следует изменить на 
. Для неориентированных мультиграфов определение 
следует изменить на 
. Чтобы избежать двусмысленности, эти типы объектов можно назвать неориентированными циклами разрешения простого графа и циклами разрешения неориентированного мультиграфа соответственно.
и обычно считаются конечными, и многие из хорошо известных результатов неверны (или сильно отличаются) для бесконечных графов, потому что многие из аргументов терпят неудачу в бесконечном случае . Более того, часто считается непустым, но может быть пустым набором. Порядок графа называется 
, его количество вершин. Размер графа называется 
, его количество ребер. Степень или валентность вершины есть число ребер, инцидентных к нему, где петля подсчитанных дважды.
В неориентированном простом графе порядка n максимальная степень каждой вершины равна n - 1, а максимальный размер графа равен n ( n - 1) / 2 .
Ребра неориентированного простого графа, допускающие петли 
индуцируют симметричное однородное отношение ~ на вершинах }что называется отношение смежности из . Конкретно для каждого ребра 
, его конечные точки и }называются смежными друг с другом, что обозначается ~ .
Направленный граф
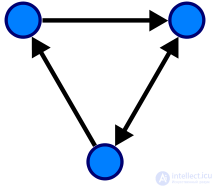
Ориентированный граф с тремя вершинами и четырьмя направленными ребрами (двойная стрелка представляет ребро в каждом направлении).
Ориентированный граф или орграф представляет собой граф , в котором ребра имеют ориентацию.
В одном ограниченном , но очень общем смысле этого термина, ориентированный граф является упорядоченной парой в составе:
, А набор из вершин (также называемые узлами или точки );
, А набор из ребер (также называемые ориентированных ребер , направленные ссылки , направленные линии , стрелка или дуги ) , которые упорядоченные пары вершин (то есть, ребро связанно с двумя различными вершинами).Во избежание двусмысленности этот тип объекта можно назвать именно ориентированным простым графом .
В краю направлено из к , вершины и называются концами ребра, хвост края и }глава края. Об этом говорит сайт https://intellect.icu . Говорят, что край соединяется и быть инцидентом на и дальше . Вершина может существовать в графе и не принадлежать ребру. Край 
называется перевернутый край из . Множественные ребра , недопустимые в соответствии с приведенным выше определением, - это два или более ребра с одинаковым хвостом и одинаковой головой.
В более общем смысле этого слова, допускающего наличие нескольких ребер, ориентированный граф - это упорядоченная тройка в составе:
, А набор из вершин (также называемые узлами или точки );, А набор из ребер (также называемых ориентированных ребер , направленных ссылок , направленных линий , стрелок или дуг );
, функция инцидентности, отображающая каждое ребро в упорядоченную пару вершин (то есть ребро связано с двумя различными вершинами).Во избежание двусмысленности этот тип объекта можно назвать именно ориентированным мультиграфом .
Цикл является ребром , который соединяет вершину саму с собой. Направленные графы, как определено в двух определениях выше, не могут иметь циклов, потому что цикл, соединяющий вершину самому себе является ребром (для ориентированного простого графа) или инцидентно (для ориентированного мультиграфа) 
которого нет в 
. Поэтому, чтобы разрешить циклы, определения должны быть расширены. Для ориентированных простых графов определение следует изменить на 
. Для направленных мультиграфов определение следует изменить на 
. Чтобы избежать двусмысленности, эти типы объектов можно назвать в точности ориентированным простым графом, разрешающим циклы, и ориентированным мультиграфом, разрешающим циклы (или колчаном ) соответственно.
Ребра ориентированного простого графа, допускающие петли является однородным отношением ~ на вершинах что называется отношение смежности из . Конкретно для каждого ребра , его конечные точки и называются смежными друг с другом, что обозначается ~ .
Существуют различные способы хранения графов, каждый из которых подходит под разные задачи и типы графов (разреженные, плотные, ориентированные, неориентированные и т.д.). Ниже — основные способы с кратким описанием, преимуществами и недостатками.
Описание:
Квадратная матрица n x n, где n — количество вершин.
Ячейка [i][j] содержит:
1 (или вес) — если есть ребро из i в j
0 — если ребра нет
Преимущества:
Быстрый доступ O(1) к информации о наличии ребра
Удобно для плотных графов
Недостатки:
Занимает O(n²) памяти — неэффективно для разреженных графов
Описание:
Для каждой вершины хранится список всех соседних вершин (в виде массива, списка или хэш-таблицы).
Пример:
A: B, C B: A C: A
Преимущества:
Компактное хранение: O(n + m) где m — число ребер
Удобно для разреженных графов
Недостатки:
Поиск наличия конкретного ребра занимает O(k), где k — степень вершины
Описание:
Просто список всех ребер как пар (или троек, если взвешенный граф):
(A, B), (A, C), (B, C) или (A, B, 3) — если вес 3
Преимущества:
Простой и универсальный формат
Удобен для перебора ребер
Недостатки:
Медленный поиск конкретных ребер
Неэффективен для некоторых алгоритмов
Описание:
Матрица n x m, где n — вершины, m — ребра.
Если вершина i инцидентна ребру j, то ячейка [i][j] = 1 (или -1, если направленный граф).
Преимущества:
Четко отражает связи вершина–ребро
Подходит для теоретических задач и матричных вычислений
Недостатки:
Занимает много памяти
Не так интуитивно понятна, как список смежности
Описание:
Для ориентированных графов: для каждой вершины хранятся входящие и/или исходящие вершины отдельно.
Удобно, когда важно различать направления.
Вершины: A, B, C Ребра: (A, B), (A, C)
Матрица смежности:
A B C A 0 1 1 B 1 0 0 C 1 0 0
Список смежности:
A: B, C B: A C: A
Список ребер:
(A, B), (A, C)
Граф можно задать как упорядованную пару множеств:
G=(V,E)где:
V — множество вершин (nodes)
E⊆V ×V — множество ребер (edges)
E⊆{{u,v}∣u,v∈V, u=v}
Ребра — неупорядованные пары
Пример:
V={A,B,C}E={{A,B},{A,C}}
}E⊆{(u,v)∣u,v∈V}
Ребра — упорядованные пары
Пример:
V={A,B,C}
E={(A,B),(A,C)}
Дополнительно задается функция весов:
}w:E→RПример:
V={A,B,C}
E={(A,B),(B,C)}
w(A,B)=3,
w(B,C)=5
Формально и однозначно
Удобно для доказательств и математических рассуждений
Основа для построения других представлений (матриц, списков и т.п.)
Вот как можно представить граф в виде структуры класса FSM (Finite State Machine) — конечного автомата — на языке программирования, например на Python, с учетом всех представлений (включая теорию множеств).
Состояния — вершины графа (V)
Переходы — ребра графа (E)
Переходы могут быть направленными (как в ориентированном графе)
Могут быть взвешенными (если добавить события, действия или веса)
Вот как можно реализовать граф в виде FSM (конечного автомата) на — JavaScript, в стиле классов ES6.
class FSM {
constructor() {
this.states = new Set(); // Множество вершин (состояний)
this.transitions = new Map(); // Отображение: fromState -> Map(toState -> event)
}
addState(state) {
this.states.add(state);
if (!this.transitions.has(state)) {
this.transitions.set(state, new Map());
}
}
addTransition(fromState, toState, event = null) {
this.addState(fromState);
this.addState(toState);
this.transitions.get(fromState).set(toState, event);
}
getStates() {
return Array.from(this.states);
}
getTransitions() {
const result = [];
for (const [from, edges] of this.transitions.entries()) {
for (const [to, event] of edges.entries()) {
result.push({ from, to, event });
}
}
return result;
}
print() {
console.log("States:", this.getStates());
console.log("Transitions:");
for (const { from, to, event } of this.getTransitions()) {
console.log(` ${from} → ${to} ${event ? `(event: ${event})` : ''}`);
}
}
}
const fsm = new FSM();
fsm.addTransition("A", "B", "go_to_B");
fsm.addTransition("A", "C", "go_to_C");
fsm.print();
Вывод в консоль:
States: [ 'A', 'B', 'C' ] Transitions: A → B (event: go_to_B) A → C (event: go_to_C)
// Множество состояний: const V = new Set(["A", "B", "C"]); // Множество переходов (ребер как упорядованные пары): const E = new Set([ ["A", "B"], ["A", "C"] ]); // Веса или события переходов: const w = new Map([ [["A", "B"], "go_to_B"], [["A", "C"], "go_to_C"] ]);
JavaScript не поддерживает множества пар напрямую, но концептуально это приближает к записи графа как:
G=(V,E),
w:E→События
| Задача | Рекомендуемый способ |
|---|---|
| Поиск соседей | Список смежности |
| Проверка наличия ребра | Матрица смежности |
| Частые операции с ребрами | Список ребер |
| Теоретический анализ | Матрица инцидентности |
Графы могут использоваться для моделирования многих типов отношений и процессов в физических, биологических, социальных и информационных системах. Многие практические задачи можно представить в виде графов. Подчеркивая их применение к системам реального мира, термин сеть иногда определяется как обозначение графа, в котором атрибуты (например, имена) связаны с вершинами и ребрами, а субъект, который выражает и понимает системы реального мира как сеть. называется сетевой наукой .
В информатике графы используются для представления сетей связи, организации данных, вычислительных устройств, потока вычислений, состоянийи их переходов и т. д. Например, ссылочная структура веб-сайта может быть представлена ориентированным графом, в котором вершины представляют веб-страницы. а направленные края представляют собой ссылки с одной страницы на другую. Аналогичный подход может быть применен к проблемам в социальных сетях , путешествиях, биологии, проектировании компьютерных микросхем, картировании прогрессирования нейродегенеративных заболеваний и многих других областях. Поэтому разработка алгоритмов для работы с графами представляет большой интерес для информатики. Трансформации графы часто формализуется и представляется системами перезаписи графов . Дополнением к системам преобразования графов, ориентированным на манипулирование графами в памяти на основе правил, являются графовые базы данных, ориентированные на безопасное для транзакций , постоянное хранение и выполнение запросов к структурированным данным графа .
Теоретико-графические методы в различных формах оказались особенно полезными в лингвистике , поскольку естественный язык часто хорошо поддается дискретной структуре. Традиционно синтаксис и композиционная семантика следуют древовидным структурам, выразительная сила которых заключается в принципе композиционности , моделируемой в виде иерархического графа. Более современные подходы, такие как грамматика структуры фраз, управляемой заголовком, моделируют синтаксис естественного языка с использованием типизированных структур признаков , которые представляют собой направленные ациклические графы . В лексической семантикеособенно применительно к компьютерам, моделирование значения слова легче, когда данное слово понимается в терминах связанных слов; Поэтому семантические сети важны в компьютерной лингвистике . Тем не менее, другие методы в фонологии (например, теория оптимальности , которая использует решетчатые графы ) и морфологии (например, морфология конечного состояния, использующая преобразователи конечного состояния ) распространены при анализе языка как графа. Действительно, полезность этой области математики для лингвистики принесла такие организации, как TextGraphs , а также различные проекты «Сети», такие как WordNet , VerbNet и другие.
продолжение следует...
Часть 1 Граф, Теория графов, история, классификация, описание, применение
Часть 2 - Граф, Теория графов, история, классификация, описание, применение
А как ты думаешь, при улучшении теория графов, будет лучше нам? Надеюсь, что теперь ты понял что такое теория графов, графы, граф, способы описания графов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.