Лекция
Сразу хочу сказать, что здесь никакой воды про декомпозиция графов, и только нужная информация. Для того чтобы лучше понимать что такое декомпозиция графов, пути в графах, кратчайшие пути , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
Из истории. Широко известны многие декомпозиции специального вида. Актуальность таких методов подтверждается, например, историей знаменитой сильной гипотезы Бержа (1962), которая продержалась 40 лет и была доказана в 2002 г. на основе декомпозиционных методов.
Декомпозиция графа – это покрытие его частями, удовлетворяющее некоторым специальным условиям. Условия могут быть совершенно разными и определяться задачами, на решение которых и ориентирована декомпозиция.
Различают классическую декомпозицию графов и алгебрачическую декомпозицию графов.
Рассмотрим алгебраическуюдекомпозицию графов. Алгебраичность новой теории декомпозиции заключается в том, что множество графов превращается в алгебраическую систему с действующей на ней полугруппой операторов. Умножение в полугруппе теоретико-категорное: операторы перемножаются как морфизмы. Операторами служат, грубо говоря, сами графы. В общей алгебре это старая испытанная идея, но в теории графов – явление новое. Результатом этих построений является декомпозиция произвольного графа на части, «похожая» на каноническое разложение натурального числа, поэтому и новая декомпозиция называется канонической
В теории графов декомпозиция на ветви неориентированного графа G — это иерархическая кластеризация ребер графа G, представленная некорневым бинарным деревом T с ребрами из G в качестве листьев. Удаление любого ребра из T делит ребра графа G на два подграфа, а шириной декомпозиции считается максимальное число общих вершин в любом подграфе, полученным таким образом. Ширина ветвления графа G — это минимальная ширина любой декомпозиции графа G на ветви.
Ширина ветвления тесно связана с древесной шириной — для всех графов они находятся в пределах постоянного множителя друг от друга и обе величины могут быть описаны запрещенными минорами. Как и для древесной ширины, многие задачи оптимизации на графах могут быть эффективно решены на графах с малой шириной ветвления. Однако, в отличие от древесной ширины, ширина ветвления планарного графа может быть вычислена точно за полиномиальное время. Декомпозиция на ветви и ширина ветвления могут быть обобщены с графов на матроиды.
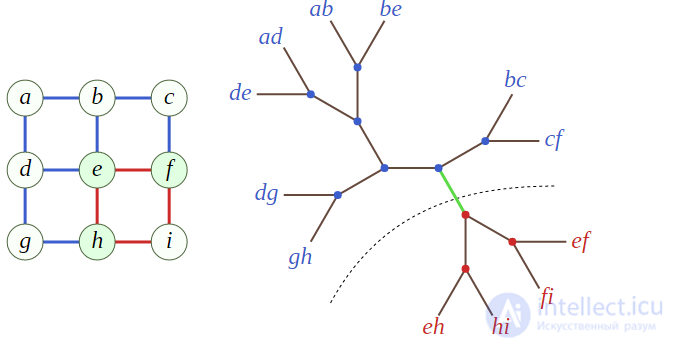
Декомпозиция на ветви решетки. Показано e-разделение. Разделение, декомпозиция, и сам граф имеют ширину три.
Путем (маршрутом,англ. path) в графе называется последовательность вида 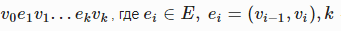 — длина (англ. length) пути.
— длина (англ. length) пути.

Путь в графе это конечная последовательность вершин, в которой каждые две вершины идущие подряд соединены ребром. Путь может быть ориентированным или неориентированным в зависимости от графа. На рис 1.а, путем является например последовательность [(1), (4), (5)] на рис 1.б, [(1), (3), (4), (5)].
Длина пути — количество ребер, входящих в последовательность, задающую этот путь.
Циклическим путем (англ. closed walk) в ориентированном графе называется путь, в котором v0=vk
Циклическим путем в неориентированном графе называется путь, в котором 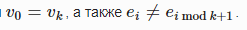
Цикл (англ. integral cycle) — это класс эквивалентности циклических путей на отношении эквивалентности таком, что два пути эквивалентны, если
 — это две последовательности ребер в циклическом пути.
— это две последовательности ребер в циклическом пути.
Простой (вершинно-простой) путь (англ. simple path) — путь, в котором каждая из вершин графа встречается не более одного раза.
Реберно-простой путь — путь, в котором каждое из ребер графа встречается не более одного раза.
Путь, для которого никакие ребра графа не соединяют две вершины пути, называется индуцированным путем.
Простая цепь, содержащая все вершины графа без повторений, известна как Гамильтонов путь.
Простой цикл, содержащий все вершины графа без повторений, известен как Гамильтонов цикл.
Цикл, получаемый добавлением ребра графа к остовному дереву исходного графа, известен как Фундаментальный цикл.
Два пути вершинно независимы, если они не имеют общих внутренних вершин. Аналогично два пути реберно независимы, если они не имеют общих внутренних ребер.
Длина пути — это число ребер, используемых в пути, при этом многократно используемые ребра считаются соответствующее число раз. Длина может равняться нулю, если путь состоит из одной только вершины.
Взвешенный граф ставит в соответствие каждому ребру некоторое значение (вес ребра). Весом пути во взвешенном графе называется сумма весов ребер пути. Иногда вместо слова вес употребляется цена или длина.
Зада́ча о кратча́йшем пути́ — задача поиска самого короткого пути (цепи) между двумя точками (вершинами) на графе, в которой минимизируется сумма весов ребер, составляющих путь.
Задача о кратчайшем пути является одной из важнейших классических задач теории графов. Сегодня известно множество алгоритмов для ее решения[⇨].
У данной задачи существуют и другие названия: задача о минимальном пути или, в устаревшем варианте, задача о дилижансе.
Значимость данной задачи определяется ее различными практическими применениями[⇨]. Например, в GPS-навигаторах осуществляется поиск кратчайшего пути между двумя перекрестками. В качестве вершин выступают перекрестки, а дороги являются ребрами, которые лежат между ними. Если сумма длин дорог между перекрестками минимальна, тогда найденный путь самый короткий.
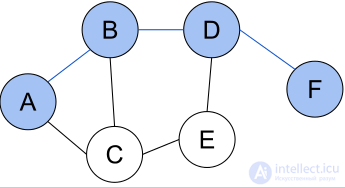
Кратчайший путь (A, B, D, F) между вершинами A и F в неориентированном графе без весов.
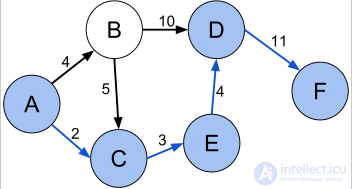
Кратчайший путь (A, C, E, D, F) между вершинами A и F во взвешенном ориентированном графе.
Общая теория:
У нас есть граф G=(V,E), где связь между вершинами v и w следующая: a(v,w) 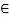 E. Если связь между вершинами отсутствует, то a(v,w)=
E. Если связь между вершинами отсутствует, то a(v,w)=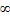 .
.
Если последняя вершина wo, w1, …, wn определяет путь в графе, то его длина равна суммарному весу входящих вершин:
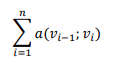
Наша задача – нахождение кратчайшего пути между вершинами S, t. M(S,t) – расстояние между S и t. Путь из S в t, который имеет минимальную длину – есть кратчайший путь, между вершинами S и t. d(S,t)=d(S,vk) + a(vk,t)
d(S,vk)=d(S,vk-1)+a(vk-1,vk)

Поиск кратчайшего пути в бесконтурном графе:
Бесконтурный орграф (Acyclic graph, DAG) — орграф, не содержащий контуров, но возможно, имеющий циклы (см. цикл в орграфе). В англоязычной литературе встречается в виде аббревиатуры DAG от Directed Acyclic Graph.
Отсюда другое название — Ациклический граф, ДЭГ.
пример безконтурного графа
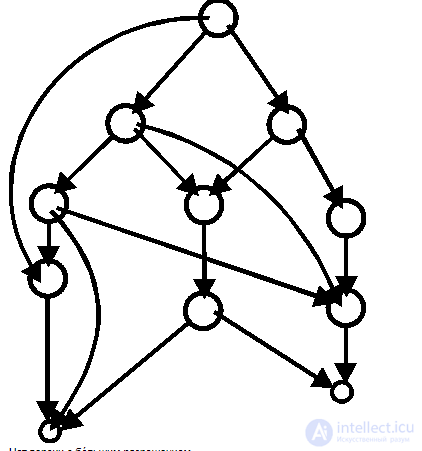
Поиск кратчайшего пути в бесконтурном графе имеет 2 части. Первая переименование вершин графа так, что первая вершина не имеет входящих вершин. Вторая часть сам поиск кратчайших путей.
Для начала зададим произвольный бесконтурный граф с произвольной нумерацией и весами.
И запишем его в виде матрице смежности, где ребра которые не входят в другие ребра будем отмечать максимально большим числом 32767.
Для перенумерации графа, так чтобы вершина №1 имела только исходящие ребра, используем алгоритм Topolsoft.
Алгоритм Topolsoft (G,N)

После чего получим следующую нумерацию графа.

Алгоритм поиска наикратчайших путей.
После можно найти кратчайшие расстояния от вершины №1 до каждой из вершин по алгоритму DSP.
Алгоритм DSP(G, N, d)
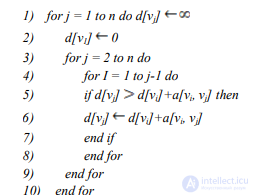
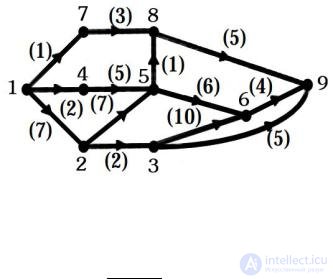
После выводим на экран результат. При этом вычислительная сложность считаем следующим образом:
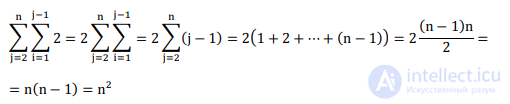
И она составит: O(n2)
Задача декомпозиции формулируется так:задан граф, для которого необходимо определить, является ли он произведением двух графов. В случае положительного ответа нужно найти графы - сомножители.
Семантика задачи. Описана система, функционирующая во времени. Необходимо определить, нельзя ли ее представить в виде системы из двух независимых блоков, как описано выше. В этом случае систему можно описать гораздо проще. Так, если система имеет 100 состояний, то при положительном решении она будет описываться как два блока, каждый из которых имеет только десять состояний.
В ранее было показано, что если граф представим произведением, то его матрица будет иметь вид правильной клеточной матрицы.
Рассмотрим еще раз пример, приведенный в предыдущем разделе в табл. 3.10.
Предположим, что в системе состояния пронумерованы следующим образом:
1=(1aa), 2=(1bb), 3=(3bb), 4=(2bb), 5=(3aa), 6=(2aa), то естьт.е. 3-ю
и 6-ю вершины поменяем местами. Тогда таблица примет видПолучим табл. 3.11.
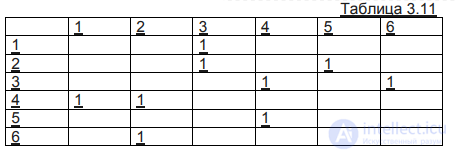
Эта таблица уже не будет правильной клеточной матрицей, хотя она описывает граф, совпадающий с исходным с точностью до имен вершин.
Значит, если матрица графа не является правильной клеточной матрицей, но может быть получена из нее путем переименования вершин, то такой граф будет представлять собой произведение графов.
Есть еще один простой критерий того, что граф не является произведением. Если Q=<C,T>, G=<A,R>, H=<B,S>, и Q=GxH, то имеет место условие:
|C|=|A|×|B|. Значит, если число вершин n графа есть простое число, то он не может быть представлен произведением графов.
Если n не простое и может быть выражено как n=kr , где k и r больше 1, то можно ставить задачу проверки этого графа на возможность представить его в виде произведения. Если граф содержит n вершин, то для проверки его необходимо в общем случае провести n! переименований. Уже для n=6 это число составит 720, для n=8 уже более 40000. Поэтому возникает необходимость сокращения объема вычислений.
Возможность сокращения основана на следующем утверждении. Если граф представлен в виде правильной клеточной матрицы, то при переименовании вершин, связанных с переименованием вершин в одном графе-сомножителе, матрица останется правильной клеточной матрицей. Точно так же, если матрица не является правильной клеточной, то перестановка имен, связанная с изменением имен в одном графе-сомножителе, ее правильной не сделает. Об этом говорит сайт https://intellect.icu . Это значит, что если n=k×r, то необходимый перебор вариантов можно сократить в k!×r! раз. Например, перебор для n=6 сократится до 60 (6=2×3, сокращение в 2!×3!=12 раз).
Алгоритм декомпозиции
Рассмотрим еще раз операцию произведения. Если вершина а в первом графе-сомножителе имеет степень захода Da, а вершина b во втором графе имеет степень захода Db, в результирующем графе вершина (a,b) будет иметь степень захода (DaDb). То же самое можно сказать и о степени исхода результирующего графа.
Алгоритм основан на том, что для каждой i –той вершины графа определяются все возможные разложения ее степеней захода si=ri×ti, т.е. предполагается, что если задача решается и этой вершине сопоставлена пара (х,у), то эти вершины имеют степени захода ri и ti соответственно. То же самое относится к степени исхода вершины i: ti=pi×qi.
Проведем разложения для всех степеней вершин. Построим два разбиения вершин: разбиение на к классов по l элементов p=(p1,p2,…,pк) и разбиение на l классов по кэлементов r=(r1, r2, …, rl), n=k×l, чтобы произведением этих разбиений было разбиение на одноэлементные множества.
В один класс p попадут вершины а и b, если для них в разложении raa=rbb и paa=pbb.
В один класс r попадут вершины а и b, если в разложениях taa=tb и qa=qb.
Если такие разбиения построить можно, то ему сопоставляется перестановка элементов по следующему правилу. Зафиксируем порядок блоков в разбиениях p и r. Сопоставим этому порядку перестановку: вначале старшинство определяется по разбиению p, затем внутри этих блоков - по разбиению r.
Рассмотрим метод на примере. Пусть граф описывается матрицей табл. 3/.12, разложения разложения s и t приведены в этой таблице. Значение степени, равное 0, представляется произведением 0 на произвольное число, обозначаемое как х. Первой задачей является задача выбора среди разложений тех, которые приведут к разбиениям вершин по степеням исхода и захода.
При выборе разложений будем учитывать следующее.
Для вершины 4 выбираем разбиение 2×2, так как вершиныу с сомножителем 4 в пару не найти. В разложения p вершины 4 и 5 должны быть в разных блоках, так как у них обе компоненты по s разные. То же самое по отношению t для вершин 3 и 4. Значит, 3 и 5 будут в одном блоке. Вершины 3 и 6 должны быть в одном блоке по t и в разных блоках по s, 1 и 5 – в разных блоках по t, чтобы по первой компоненте их можно было объединить в разложении r. Курсивом выделены разбиения. В итоге получаем разложение p={{1,4,6}, {2,3,5}}.

После этого однозначно получаем r={{1,5},{3,6},{2,4}}.
Зафиксируем порядок в этих разбиениях. Тем самым мы предполагаем, что если решение существует, то граф можно представить произведением двух графов, один из которых содержит 2 вершины (пусть, например, вершины а и b), второй содержит три вершины (пусть, например, 1, 2 и 3). Тогда вершинам первого блока разбиения p сопоставлены элементы декартова произведения с вершиной а в качестве первого слагаемого, для вершин второго блока первым слагаемым будет b.
Аналогично в соответствующем декартовом произведении вторым сомножителем для вершин первого блока разбиения r будет вершина 1, второго блока – вершина 2, третьего блока – вершина 3. Составим разбиениям p и r упорядочение <1,4,6,5,2,3>, которое «испортило» матрицу, исправим ее, используя обратное упорядочение
1 2 3 4 5 6
1 5 6 2 4 3.
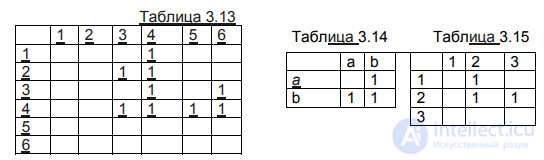
Применим эту перестановку к матрице, получим табл.3.13. Как видно из таблицы, она является правильной клеточной матрицей, что приводит к решению: граф представим произведением двух графов, матрицы смежности которых легко получаются из табл. 3.13 Матрицы графов-сомножителей представлены в табл. 3.14 и 3.15.
Пример заданий
Для заданного графа определить, разложим ли он в произведение двух графов. Если разложим, то найти графы – сомножители.

Отличительными особенностями графов, возникающих в современных приложениях, являются их большая размерность и разреженность. Ускорение работы любого из известных алгоритмов решения оптимизационных задач на графах может быть достигнуто за счет предобработки исходного графа. Технология предобработки реализуется, как правило, в виде двухфазной процедуры. На первой фазе производится предобработка графа путем его редуцирования или декомпозиции. Выбор вида предобработки определяется особенностями решаемой задачи и структурой графа. На второй фазе обычно применяется известный алгоритм решения задачи к преобразованному графу и формируется решение для исходного графа. При этом требуется, чтобы предобработка существенно снижала размерность задачи, обеспечивала корректность формирования решения задачи исходя из одного или нескольких решений, полученных для преобразованного графа, вычислительная сложность предобработки не превышала сложности решения рассматриваемой задачи на исходном графе.
Реализация декомпозиционного подхода, то есть процесса выделения частей исходного графа, во многом зависит от структурных особенностей этого графа, в том числе от ограничений на параметры, характеризующие его разреженность. Один из параметров разреженности графа - ограничение на его древовидную ширину [1, 2]. Для графов с ограниченной древовидной шириной используется разложение графа кликовыми минимальными сепараторами. Идея такого разложения была предложена Р. Тарьяном как средство реализации принципа «разделяй и властвуй» для решения NP-трудных задач на графах, базирующихся на отношениях смежности вершин графа. Полученные в результате разложения части графа были названы атомами. Тарьяном установлено, что разложение графа на атомы не разрушает клики этого графа, не порождает новые клики и в этом смысле сохраняет его структуру.
В данной работе предлагаются алгоритмы и программы, практически реализующие идею Тарьяна. Демонстрируется применение данного подхода к NP-трудной задаче о клике.
Основные понятия и обозначения
Введем основные понятия и обозначения из теории графов, необходимые для изложения результатов работы. Используем терминологию и обозначения, принятые в работе .
Пусть G = (V, E) - неориентированный конечный граф с множеством вершин V и множеством ребер E. Считается, что вершины v1 и v2 графа G смежные, если {v1, v2} Î E, и несмежные в противном случае. Ребро e инцидентно вершине v1, если e = {v1, v2} Î E, и не инцидентно иначе. Если e = {v1, v2} Î E, то вершины v1 и v2 называют концами ребра e. В этом случае говорят также, что ребро e соединяет вершины v1 и v2. Два ребра считаются кратными, если их концы совпадают. Ребро, соединяющее вершину саму
с собой, называется петлей. Простой граф – неориентированный конечный граф G = (V, E) без петель
и кратных ребер. Везде далее будут рассматриваться только простые графы, для которых½V½ ³ 2 и ½E½ ³ 1.
Множество всех вершин графа G, смежных с некоторой вершиной v Î V, образует в G окрестность (или открытую окрестность) вершины v, которая обозначается через N(v). Замкнутая окрестность вершины v обозначается N[v] и определяется равенством: N[v] = N(v) È {v}. Число deg v = | N(v) | называется степенью вершины v.
Граф G¢ = (V¢, E¢) называется подграфом графа G = (V, E) при условии, что V¢ Í V, E¢ Í E. Подграф G¢ = (V¢, E¢) является остовным, когда V¢ = V. Если множество вершин подграфа G¢ есть V¢, а множество его ребер совпадает с множеством всех ребер графа G, оба конца которых принадлежат V¢, то G¢ называется подграфом, индуцированным множеством V¢ Í V, и обозначается G(V¢). Всякий максимальный по включению связный подграф графа G образует его компоненту связности. Множество вершин некоторой компоненты графа G называется областью связности этого графа.
Множество вершин V¢ называется кликой графа G, если в графе G(V¢) всякие две вершины смежные, и максимальной кликой, если она не содержится в клике с большим количеством вершин. Размер наибольшей (по числу вершин) клики графа G обозначается j(G) и называется плотностью графа G. Граф G = (V, E), являющийся кликой, называется полным графом и обозначается через Kn, где n = ½V½. Для него j(Kn) = ½V½, а в общем случае для G = (V, E) всегда 1 £ j(G) £ ½V½.
Говорят, что множество вершин S Ì V разделяет несмежные вершины u и v графа G = (V, E), если
в графе G - S = G(V \ S) вершины u и v принадлежат различным компонентам связности. Множество S при этом называется (u, v)-сепаратором и минимальным (u, v)-сепаратором, если S есть (u, v)-сепаратор и в нем нет собственного подмножества, являющегося (u, v)-сепаратором. Сепаратор S считают минимальным, если в графе G существует такая пара вершин u и v, что S - минимальный (u, v)-сепаратор. Наименьший по мощности сепаратор графа G - наименьший сепаратор. Одновершинный сепаратор называется точкой сочленения графа. Кликовый минимальный сепаратор – это минимальный сепаратор, являющийся кликой.
Граф G называется хордальным, если ни один из его индуцированных подграфов не является простым циклом длины l ³ 4. Любой граф можно превратить в хордальный, добавив в него некоторое множество ребер. Триангуляцией графа G = (V, E) называется хордальный граф H = (V, E¢), E Í E¢, который содержит G в качестве остовного подграфа. Триангуляция H - минимальная триангуляция графа G, если для G не существует другой триангуляции, которая является собственным подграфом графа H. Наименьшей считается триангуляция с наименьшим числом ребер.
Древовидная ширина (treewidth) – числовой параметр, характеризующий меру древовидности графа, то есть близости его к дереву. Древовидная ширина вычисляется через дерево декомпозиции. Под деревом декомпозиции графа G = (V, E) понимают пару (V, T), задающую определенное разбиение вершин и ребер графа G, где V = {Vi : i Î I} – семейство непустых подмножеств множества V, называемых «мешками», T = (I, W) – дерево, узлам которого сопоставлены эти «мешки». Данное разбиение удовлетворяет следующим свойствам [1, 2]:
Ширина дерева декомпозиции (M, T) – наибольшая вместимость его «мешка», уменьшенная на единицу: max{|Xi | − 1 : i Î I}. Древовидная ширина графа G определяется как наименьшая ширина всех допустимых его деревьев декомпозиции и обозначается tw(G).
Характеризация разреженных и хордальных графов
Известно несколько формальных определений разреженного графа. Связный граф G = (V, E), n = |V | ³ 2, |E | ³ 1, называют (реберно) разреженным, если число его ребер удовлетворяет условию
|E| £ anb, (1)
где a > 0, 1 £ b < 2 - положительные вещественные константы. Считают, чем меньше значение b, тем более разреженным является граф G. Для сравнения: в каждом дереве число ребер равно n – 1, то есть b = 1, что отвечает нижней границе значения b, а для любого полного n-вершинного графа всегда |E| = n(n – 1) /2, то есть b = 2, что соответствует верхней границе значения b.
Существует другое определение разреженного графа G, которое выражается через древовидную ширину tw(G) этого графа. Для tw(G) верны границы: 1 £ tw(G) £ n – 1. Так, всякое n-вершинное дерево (n ³ 2) имеет единичную древовидную ширину, что отвечает нижней границе для tw(G), а полному
n-вершинному графу свойственна древовидная ширина, равная n – 1, что соответствует верхней границе для tw(G). Пусть k есть некоторая заданная положительная целая константа. Если tw(G) £ k, то говорят, что граф G = (V, E) обладает ограниченной (значением k) древовидной шириной. Считается, чем меньше значение k, тем более разреженным является граф G. Известно , если tw(G) £ k, то для числа ребер графа G = (V, E) справедливо неравенство
|E| £ kn – k(k + 1) /2. (2)
При k = 1 и k = n – 1 соотношение (2) приводит к неравенствам (1), соответствующим деревьям и полным графам. Следовательно, ограничение tw(G) £ k не противоречит (1) и задает естественную меру разреженности графа G. Учитывая, что всегда j(G) – 1 £ tw(G), можно говорить о том, что значение tw(G) ограничивает не только число ребер графа, но и размеры его клик. В дальнейшем разреженность графа G понимается в смысле ограничения tw(G) £ k.
Процесс разложения графа на атомы базируется на свойствах хордальных графов . Сформулируем наиболее важные из них в виде лемм 1–4.
Лемма 1. Граф G = (V, E) является хордальным тогда и только тогда, когда его любой минимальный сепаратор образует в G-клику.
Лемма 2. Связный граф G = (V, E) хордальный тогда и только тогда, когда для него существует дерево клик, определяемое так: множество узлов дерева - множество {Ci : i Î J} всех максимальных клик графа G; два узла Ci, Cj соединены ребром, если соответствующие им клики графа G имеют непустое пересечение, то есть Ci Ç Cj ¹ Æ; для любой вершины v Î V графа G множество максимальных клик, содержащих эту вершину, индуцирует связный подграф, являющийся поддеревом дерева клик.
Поскольку всякий связный хордальный граф G = (V, E) имеет не более n - 1 максимальных клик, то, согласно лемме 2, его дерево клик содержит не более n - 1 узлов, где n = |V |.
Лемма 3. Связный хордальный граф G = (V, E) может иметь несколько различных деревьев клик, но каждое из них – остовное дерево наибольшего веса графа пересечений всех максимальных клик исходного графа, где вес ребра - число вершин, образующих пересечение надлежащих максимальных клик графа G.
Лемма 4. Пусть T – некоторое дерево клик связного хордального графа G. Для произвольного ребра дерева клик T, связывающего узлы Ci и Cj, пересечение Ci Ç Cj образует минимальный сепаратор графа G. Верно и обратное утверждение: если S – минимальный сепаратор графа G, то в T всегда найдется ребро, соединяющее узлы Ci и Cj, такое, что Ci Ç Cj = S.
Согласно леммам 2 и 4, в хордальном графе G = (V, E) минимальных сепараторов не более n - 2. По лемме 1 все эти сепараторы кликовые.
Формулировка задачи разложения графа на атомы
Задачу разложения графа на атомы (Decomposition of Graph into Atoms Problem, DGAP) можно сформулировать следующим образом:
Decomposition of Graph into Atoms Problem.
Заданы: связный граф G = (V, E), для которого ½V½ ³ 2, ½E½ ³ 1, tw(G) ≤ k, то есть древовидная ширина ограничена некоторой малой по значению константой k > 0, а также множество всех кликовых минимальных сепараторов D(G) этого графа.
Требуется: найти для G множество атомов W(G) = {G1, G2, ..., Gp}, где каждый атом Gi, i = 1, …, p, определяется как максимальный связный подграф графа G, не имеющий кликовых минимальных сепараторов графа G.
Множество W(G) принято называть атомарным представлением (или разложением на атомы) графа G.
Доказано [3, 5], что задача DGAP полиномиально разрешима и имеет единственное решение. Последнее означает, что множество атомов W(G) уникально для G, если разложение осуществлять на основе D(G) - множества всех кликовых минимальных сепараторов графа G. Если в D(G) имеются минимальные сепараторы, не являющиеся кликами в G, то W(G) может зависеть как от состава D(G), так и от порядка просмотра сепараторов в процессе разложения. Следует заметить, что число минимальных сепараторов графа, как правило, больше числа его кликовых минимальных сепараторов, и только для хордовых графов имеет место равенство. В общем случае граф G = (V, E) может иметь экспоненциальное число минимальных сепараторов относительно n = |V|, тогда как в хордовом графе их всегда не более n - 2. Заметим, что кликовые минимальные сепараторы могут пересекаться как множества вершин. Возможна вложенность кликовых минимальных сепараторов один в другой, поскольку каждый из них может быть минимальным относительно различных пар вершин графа. Примечательно, что не каждый граф обладает сепараторами, в том числе и кликовыми минимальными сепараторами: например, сепараторов нет в полном графе.
Следует отметить, что атомарное представление W(G) графа G = (V, E) является обобщением разложения его на блоки: когда множество кликовых минимальных сепараторов D(G) состоит лишь из точек сочленения графа G, то каждый атом из W(G) представляет собой блок этого графа. Напомним, что блок графа – максимальный относительно включения связный подграф графа G, не имеющий точек сочленения.
Способы вычисления кликовых минимальных сепараторов
Для определения уникального набора атомов W(G) заданного графа G = (V, E) надо предварительно найти множество D(G) всех кликовых минимальных сепараторов графа G. Такой набор сепараторов легко вычисляется для хордального графа с использованием лемм 1–4. Однако в общем случае существуют два способа нахождения D(G):
– найти все минимальные сепараторы, а затем среди них выделить те, которые образуют клики в G;
– извлечь кликовые минимальные сепараторы из минимальной триангуляции H графа G.
Рассмотрим вначале первый способ. Известно , что множество S Í V является минимальным сепаратором графа G = (V, E), если и только если существуют две различные области связности D1 и D2 графа G - S, такие, что
N (D1) = N (D2) = S, (3)
N (Di) = (È v Î Di N (v)) \ Di, i = 1, 2.
Напомним, что граф G - S получается из G удалением всех вершин из S Í V. Необходимое и достаточное условие (3) позволяет находить в графе G все минимальные сепараторы через близкие сепараторы. Минимальный (u, v)-сепаратор S, для которого S Í N(v), называется минимальным сепаратором, близким к вершине v. Для произвольной вершины v Î V графа G = (V, E) можно вычислить близкие к ней минимальные сепараторы следующим образом:
– определить множество вершин N [v];
– построить граф G - N [v] и выявить в нем все области связности;
– установить для всякой выявленной области связности D графа G - N [v] множество вершин N (D), образующих окрестность для D в графе G. Каждое такое множество определяет в G минимальный сепаратор, близкий к вершине v.
Исходя из определения минимальных сепараторов, можно доказать следующие свойства отношения их близости с вершинами графа. Если вершина v Î V смежна со всеми другими вершинами графа G = (V, E), то в G не существует минимального сепаратора, близкого к v. В этом случае N[v] = V и граф G - N[v] пустой. Во всех других случаях могут существовать несколько минимальных сепараторов, близких к v. Возможны случаи, когда один и тот же минимальный сепаратор близок к различным несмежным вершинам графа. При этом если u и v не являются смежными вершинами, то существует ровно один минимальный (u, v)-сепаратор, близкий к v. Кроме того, для всякого минимального сепаратора графа G = (V, E) всегда найдется хотя бы одна вершина v Î V, к которой он близок. Эти свойства
минимальных сепараторов указывают стратегию их перебора: начиная с некоторого множества минимальных сепараторов можно это множество последовательно пополнять путем выявления минимальных сепараторов, близких к вершинам, входящим в ранее обнаруженные минимальные сепараторы. Подробно алгоритм генерации всех минимальных сепараторов графа представлен в работе . Ясно: если граф имеет экспоненциальное число сепараторов, то данный способ вычисления D(G) может быть чрезмерно затратным по времени для графов большой размерности.
Второй способ - извлечение всех кликовых минимальных сепараторов из минимальной триангуляции H графа G - единственный на сегодняшний день эффективный (полиномиальный по времени) способ построения D(G) для графа G. Заметим, что задача нахождения наименьшей триангуляции является NP-трудной . Между тем для произвольного графа G всегда можно построить за полиномиальное время некоторую минимальную (не обязательно наименьшую) триангуляцию H, при этом tw(G) £ tw(H) [1, 2]. Знание хотя бы одной минимальной триангуляции H для исходного графа G позволяет найти для G набор всех его кликовых минимальных сепараторов. Об этом свидетельствует следующее утверждение.
Утверждение [3, 5]. Пусть заданы граф G = (V, E) и некоторая его минимальная триангуляция H = (V, E′), E Í E′. Все минимальные сепараторы графа H являются минимальными сепараторами графа G.
Из данного утверждения следует, что кликовые минимальные сепараторы графа G можно определять путем анализа минимальных сепараторов хордального графа H и выделения среди них тех, которые образуют клики в G.
Алгоритм разложения графа на атомы и свойства атомов
Алгоритм разложения графа на атомы (далее алгоритм MakeAtoms), включая вычисление множества D(G) всех кликовых минимальных сепараторов графа G, сводится к выполнению следующей последовательности шагов.
Шаг 1. Нахождение для исходного графа G = (V, E) минимальной триангуляции H = (V, E¢), E Í E¢.
Шаг 2. Поиск всех максимальных клик в триангуляции H.
Шаг 3. Построение дерева клик для триангуляции H (с использованием лемм 2 и 3).
Шаг 4. Установление множества минимальных сепараторов D(H) для триангуляции H (по леммам 1 и 4). Вычисление для графа G множества кликовых минимальных сепараторов D(G) путем выделения из D(H) тех сепараторов, которые образуют клики в G (согласно утверждению).
Шаг 5. Непосредственное формирование множества атомов W(G) на основе D(G).
Шаги 1 и 2 алгоритма MakeAtoms реализуются с помощью известного алгоритма MCS-M, который находит для G минимальную триангуляцию H и все максимальные клики в H, затрачивая на это время O(n3) . На шаге 3 осуществляется построение дерева клик для связного хордального графа H, исходя из графа пересечения всех его максимальных клик, с применением классического алгоритма построения оптимального остова за время O(n2) . Шаги 3, 4 основаны на свойствах хордальных графов и утверждении. Согласно свойствам хордальных графов, минимальные сепараторы для H находятся через точки сочленения дерева клик и их число не превышает n - 2. Кроме того, каждый минимальный сепаратор минимальной триангуляции H является минимальным сепаратором для входного графа G. Значит, D(G) Í D(H). Поскольку граф H хордальный, любой сепаратор из D(H) образует клику в H, но необязательно клику в G. Между тем всякий кликовый минимальный сепаратор графа G всегда входит в D(H) независимо от выбранной на шаге 1 минимальной триангуляции H. В целом для нахождения D(G) требуется время O(n3). На шаге 5 выполняется непосредственное формирование множества W(G). Процесс выполнения этого шага сводится к многократному разделению графа G на части одним из кликовых минимальных сепараторов S Î D(G), выделению компонент связности графа G - S и копированию S в эти компоненты. Этот процесс продолжается до тех пор, пока в полученных частях не окажется кликовых минимальных сепараторов из D(G). Время выполнения шага 5 составляет O(n3). Значит, исполнение алгоритма MakeAtoms требует O(n3) времени.
Для приложений существенны следующие особенности атомов, формируемых алгоритмом MakeAtoms:
– всякий атом из W(G) является порожденным подграфом графа G;
– количество атомов в W(G) не превосходит числа вершин графа G;
– если G является хордальным графом, то каждый атом из W(G) образует клику в G;
– множество W(G) сохраняет все клики графа G, то есть всякая клика графа G становится кликой одного из его атомов. Верно и обратное: все клики атомов являются кликами графа G, новых клик при разложении не возникает;
– атомы перекрываются, если они содержат один и тот же кликовый минимальный сепаратор, но не всякое непустое пересечение областей связности двух различных атомов W(G) является сепаратором;
– на основе множеств W(G) и D(G) возможно полное восстановление графа G путем «склеивания» атомов с помощью соответствующих кликовых минимальных сепараторов.
Пару множеств W(G) и D(G) можно рассматривать как форму представления графа большой размерности. Такое представление может быть предварительно создано за полиномиальное время и храниться во внешней памяти компьютера, а необходимые для обработки атомы последовательно загружаться в оперативную память. Основной недостаток атомарного представления графа: не все графы имеют кликовые минимальные сепараторы. Между тем, если граф G отличен от полного графа, то в нем всегда имеются минимальные сепараторы. Если при разложении воспользоваться ими, уникальность W(G) не
гарантируется, однако при tw(G) ≤ k размеры получаемых частей графа составят O(k). Будут сохранены также все клики входного графа.
Применение декомпозиционного подхода
Изложенный выше декомпозиционный подход применим для решения задач на графах, базирующихся на отношениях смежности вершин графа. Он может служить основой разработки двухфазных алгоритмов, на первой фазе которых производится предобработка входного графа путем его разложения на атомы. Как показали эксперименты, такая предобработка дает ощутимое ускорение классических алгоритмов решения NP-трудных и полиномиально разрешимых оптимизационных задач на больших разреженных графах.
Двухфазные алгоритмы были реализованы в виде программ для NP-трудной задачи о клике (Maximum-Clique-Problem, MCP), которая формулируется следующим образом :
Maximum-Clique-Problem.
Заданы: граф G = (V, E) и положительное целое число l ≤ n = |V|.
Вопрос. Верно ли, что G содержит клику размера не менее l?
Для точного решения MCP использовался алгоритм Уилфа . Данный алгоритм является рекурсивным и находит точное решение MCP за время O(poly(n) ∙ 1,39n), где poly(n) – некоторый полином от n. При двухфазной процедуре решения MCP первая фаза (алгоритм MakeAtoms - разложение графа на атомы) выполняется за время O(n3), а вторая фаза (алгоритм Уилфа для каждого атома и связывание решений) - за время O(n × poly(k) × 1,39k). Таким образом, время работы двухфазного алгоритма линейно зависит от n = |V| и экспоненциально от значения k, tw(G) ≤ k. Таким образом, чем более разреженным является граф G, тем больший эффект достигается от его предобработки при нахождении точного решения MCP с помощью алгоритма Уилфа.
Для решения задачи о клике также существует большое количество приближенных алгоритмов решения, некоторые из которых построены на жадной стратегии. Один из таких алгоритмов приведен рисунке 1. Время работы алгоритма GREEDY составляет O(n2). Применение данного алгоритма при двухфазном подходе к решению задачи MCP для разреженных графов дает оценку времени работы O(n ∙ k2).

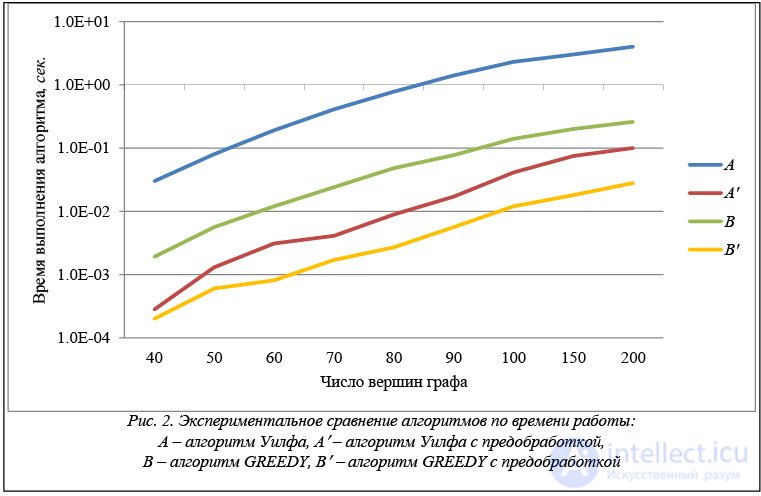
Вычислительные эксперименты, проведенные на случайных графах, подтвердили указанные выше теоретические оценки времени работы двухфазных алгоритмов и показали, что они работают значительно быстрее, чем соответствующие однофазные алгоритмы, и порядок ускорения существенно зависит от размерности и разреженности входного графа (рис. 2).
На сегодняшний день, когда объемы исследуемых данных достигают огромных размеров, востребованы алгоритмы и программы, способные обрабатывать эти данные за реальное время. В статье рассмотрен декомпозиционный подход, приводящий к ускорению работы классических алгоритмов решения
оптимизационных задач на разреженных графах большой размерности. Подход основан на разложении исходного графа на атомы кликовыми минимальными сепараторами. Атомарное представление графа может быть предварительно создано за полиномиальное время и храниться во внешней памяти компьютера, а необходимые для обработки атомы последовательно загружаться в оперативную память. В статье представлены алгоритмы и программы, реализующие построение такого представления. Перспективны дальнейшие исследования по совершенствованию рассмотренного декомпозиционного подхода, направленные на учет возможных изменений в течение времени состава вершин и ребер исходного графа, и по его применению к задачам маршрутизации в коммуникационных сетях.
А как ты думаешь, при улучшении декомпозиция графов, будет лучше нам? Надеюсь, что теперь ты понял что такое декомпозиция графов, пути в графах, кратчайшие пути и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.