Алгоритм Косарайю - поиск областей сильной связности в ориентированном графе.

Привет, Вы узнаете о том , что такое алгоритм косарайю, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое алгоритм косарайю , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

Алгоритм Косараджу(Косарайю) (в честь американского ученого индийского происхождения Самбасивы Рао Косараджу — алгоритм поиска областей сильной связности в ориентированном графе. Чтобы найти области сильной связности, сначала выполняется поиск в глубину (DFS) на обращении исходного графа (то есть против дуг), вычисляя порядок выхода из вершин. Затем мы используем обращение этого порядка, чтобы выполнить поиск в глубину на исходном графе (в очередной раз берем вершину с максимальным номером, полученным при обратном проходе). Деревья в лесе DFS, которые выбираются в результате, представляют собой сильные компоненты.

Ориентированный ациклический граф — это ориентированный граф, не содержащий направленных циклов.

Поиск компонент сильной связности стал возможен благодаря поиску в глубину на ориентированном графе. Описываемый здесь алгоритм был предложен независимо Косарайю в 1979 году.

Чтобы найти области сильной связности, сначала выполняется поиск в глубину на обращении исходного графа, вычисляя порядок выхода из вершин. Затем мы используем обращение этого порядка, чтобы выполнить поиск в глубину на исходном графе (в очередной раз берем вершину с максимальным номером, полученным при обратном проходе). Деревья в лесе DFS, которые выбираются в результате, представляют собой сильные компоненты.

Этот алгоритм, работает на двух сериях поисков в глубину(допустим обход в ширину), и потому выполняется за время O(n + m)

алгоритм косарайю

1. Инвертируем дуги исходного ориентированного графа.
2. Запускаем поиск в глубину на этом обращенном графе, запоминая, в каком порядке выходили из вершин.
3. Запускаем поиск в глубину на исходном графе, в очередной раз выбирая не посещенную вершину с максимальным номером в векторе, полученном в п.2.
4. Полученные из п.3 деревья и являются сильно связными компонентами.

Свойство

Метод Косараджу обеспечивает поиск сильных компонент связности графа за линейное время и память.

Доказательство: Этот метод состоит из двух процедур поиска в глубину, подвергнутых незначительным изменениям, в результате время его выполнения пропорционально V² в случае насыщенных графов и V + E в случае разреженных графов (если графы представлены в виде списков смежных вершин).

Лема

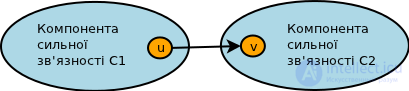
Рассмотрим два смежных компонента сильной связности в G (изображение справа). Об этом говорит сайт https://intellect.icu . Пусть f(v) – порядок завершения для вершины v в DFS-цикле. Тогда:

Доказательство используется фактом, что мета-граф (уплотненный граф) такой, в котором все компоненты сильной связности стянуты к одной вершине являются ациклическими .

Следствие: наибольшее значение f будет иметь в компоненте-источнике ( англ. source SCC ), то есть вершина будет лежать на верхушке стека.

Сложность

Если на входе граф описан с помощью списка смежности , алгоритм выполняет два полных обхода графа, следовательно выполняется за Θ(V+E) (линейное) время, оптимальное, так как совпадает с нижним пределом (каждый алгоритм должен обойти все вершины и ребра). Это концептуально самый простой эффективный алгоритм, но не столь быстрый как алгоритм Тарджана и алгоритм компонент сильной связности по путям , выполняющим лишь один обход графа.

Если граф представлен через матрицу смежности , алгоритм требует время Ο(V ² ) .

Пример и реализация

Ниже приведен пример работы алгоритма Косараджу (Косарайю).

Чтобы вычислить сильные компоненты ориентированного графа, расположенного снизу слева, мы сначала выполняем поиск в глубину на его обращении (вверху слева), вычисляя вектор обратного порядка обхода (Order). Этот порядок эквивалентен обратному порядку обхода леса DFS. Используя обращение этого порядка мы производим обход в глубину на исходном графе. То есть начинаем с вершины 3. Деревья в лесе DFS, которые выбираются в результате этого процесса, представляют собой сильные компоненты. Содержимое вектора id: номер компоненты, цифры слева — номер вершины.

Вау!! 😲 Ты еще не читал? Это зря!

• поиск в глубину
• поиск в ширину
• компонент сильной связности
• ориентированный граф
• транспонируемый граф

Исследование, описанное в статье про алгоритм косарайю, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое алгоритм косарайю и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.