Лекция
Привет, Вы узнаете о том , что такое визуализация графов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое визуализация графов, силовые алгоритмы визуализации графов , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
Визуализация или отображение графов, как ответвление теории графов, относящееся к топологии и геометрии — двумерное представление графа. В основном, это графическое представление укладки графа на плоскость (как правило, допускается пересечение ребер), направленное, обычно, на удобное отображение некоторых свойств графа, или моделируемого объекта.
Проблема визуализации графов встает, например, при отображении больших интегральных схем, анализе социальных сетей, в таких областях как картография и биоинформатика.
Графы, как правило, отображаются графически при помощи точек для представления вершин и отрезков, или ломаных, для отображения ребер между связанными вершинами. Ориентация ребра (в орграфе) отображается при помощи стрелки. При этом отображение графа не следует путать с самим графом (абстрактной, не геометрической структурой). Для каждого графа существует множество различных способов его отображения. Абстрактно, все они сводятся к способам отображения вершин и ребер. Более конкретно, важно расположение этих вершин и ребер, удобство восприятия, использования, стоимость создания и эстетические критерии.
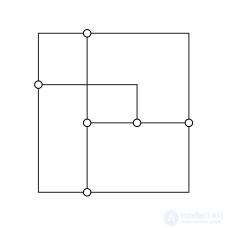
Ортогональное отображение графа
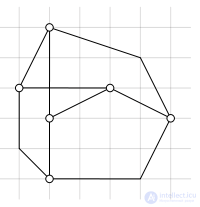
Сеточное отображение графа
В связи с большим разнообразием видов графов, существует множество различных способов отображения графов.
Например, для графов с небольшим числом вершин и сопоставимым с ним числом ребер, самым удобным может быть прямолинейное представление. Примером такой системы может служить дорожная система города. Но для графа социальной сети прямолинейного отображения, из-за большого числа дуг, будет явно недостаточно.
Можно выделить следующие способы отображения :
Эстетические критерии определяют параметры отображения. Наиболее распространенные среди них:
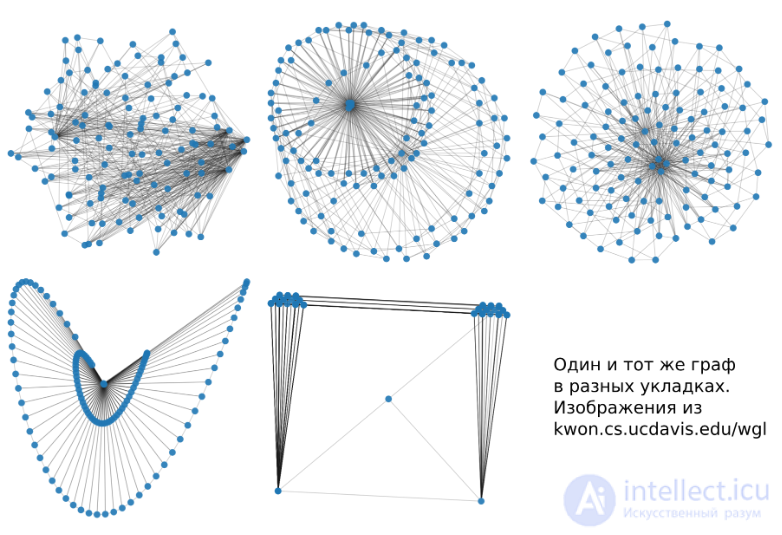
Укладка — это способ сопоставить каждой вершине графа координаты. Обычно речь идет о координатах на плоскости, хотя вообще говоря это не обязательно должна быть плоскость. Просто использовать больше чем 2 измерения почти никогда не нужно.
Наибоее важным являются эти три вида укладок, хотя классификаций и типов можно придумать много. Однако, знания этих типов достаточно, чтобы ориентироваться в предмете.
Эти методы используют симуляцию физических сил. Вершины представляются как заряженные частицы, которые отталкивают друг друга, а ребра — как упругие струны, которые стягивают смежные вершины. Потом моделируется движение вершин в такой системе, пока не установится устойчивое состояние. В других подходах пытаются описать потенциальную энергию такой системы и найти положение вершин, которое будет соответствовать минимуму.
Плюсы этого семейства алгоритмов в качестве картинки. Обычно действительно получается хорошая укладка, которая отражает топологию графа. Об этом говорит сайт https://intellect.icu . Минусы в числе параметров, которые нужно настраивать. Ну и, конечно, вычислительная сложность. Для каждой вершины нужно рассчитать силы, действующие со стороны всех других вершин.
Важные алгоритмы семейства — Force Atlas, Fruchterman-Reingold, Kamada Kawaii и OpenOrd. Последний алгоритм — использует хитрые оптимизации, например обрубает длинные ребра для ускорения вычислений, и в качестве побочного эффекта получаются более плотные кластера близких вершин.
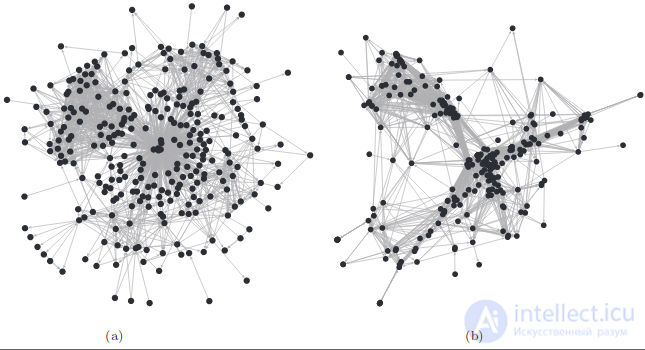
Граф можно задавать матрицей смежности, то есть квадратной матрицей NxN, где N — число вершин. Это можно интерпретировать как N объектов в пространстве размерности N. Такое представление позволяет использовать универсальные методы снижения размерности, вроде tSNE, UMAP, PCA и так далее. Другой подход основывается на том, чтобы рассчитать теоретические расстояния между вершинами, основываясь на весах ребер и знании локальной топологии, а затем попытаться сохранить соотношения между этими расстояниями при переходе в пространства меньшей размерности.
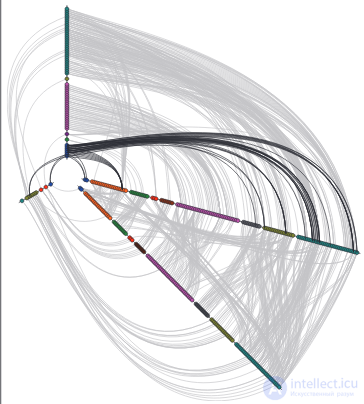
Обычно данные приходят из реального мира, где у нас есть не только информация о смежности вершин. Вершины являются какими-то реальными объектами со своими свойствами. Вспоминая об этом, мы можем использовать свойства вершин для отображения их на плоскости. Для этого можно использовать любые подходы обычно применяемые для табличных данных. Это уже упомянутые выше методы снижения размерности PCA, UMAP, tSNE, Autoencoders. Либо можно рисовать простой scatter plot (диаграмма рассеяния) для пар признаков и рисовать ребра уже поверх полученного представления. Отдельно можно упомянуть Hive Plot — интересный метод когда значениям признака соответствуют разные оси направленные из центра, на которых располагают вершины, а ребра рисуют дугами между ними.
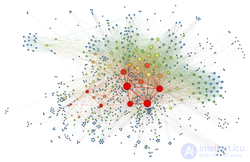
Визуализация социальной сети с помощью силового алгоритма визуализации графа
Визуализация связей страниц в Вики с помощью силового алгоритма визуализации размещения.
Силовые алгоритмы визуализации графов — класс алгоритмов визуализации графов в эстетически приятном виде. Их цель — распроложить узлы графа в двумерном или трехмерном пространстве так, что все ребра имели бы более-менее одинаковую длину, и свести к минимуму число пересечений ребер путем назначения сил для множества ребер и узлов основываясь на их относительных положениях, а затем путем использования этих сил либо для моделирования движения ребер и узлов, либо для минимизации их энергии.
В то время, как визуализация графов может оказаться трудной задачей, силовые алгоритмы, будучи физическими моделями, обычно не требуют специальных знаний в теории графов, таких как планарность графа.
Силовые алгоритмы визуализации графов назначают силы на множестве ребер и узлов графа. Обычно используются подобные пружинным силы притяжения на основе закона Гука для назначения сил парам концов ребра графа. В то же время используются силы отталкивания, подобные отталкиванию электрически заряженных частиц на основе закона Кулона, чтобы разделить все пары узлов. Для получения равновесного состоянии этой системы сил ребра стремятся получить однородные длины (ввиду действия пружин), а узлы, не связанные ребром, стремятся расположиться поодаль друг от друга (ввиду действия сил отталкивания). Силы притяжения (ребра) и силы отталкивания (узлы) могут быть определены с помощью функций, которые не основаны на физическом поведении пружин и частиц. Например, некоторые силовые системы используют пружины, силы которых меняются логарифмически, а не линейно.
Альтернативная модель рассматривает подобные пружинным силы для каждой пары узлов e (i,j) , где идеальная длина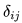 
каждой пружины пропорциональна расстоянию в графе между узлами i и j, а силы отталкивания не используются. Минимизация разницы (обычно, квадрата разницы) между евклидовым и идеальным расстоянием между узлами эквивалентна метрической задаче многомерного шкалирования.
Силовой граф может использовать силы, отличные от механических пружин и сил отталкивания зарядов. Сила, аналогичная гравитации может быть использована для притяжения вершин в сторону фиксированной точки пространства рисования графа. Это может быть использовано для сведения различных компонент связности несвязного графа в одно целое , в противном случае эти части разлетелись бы друг от друга под действием сил отталкивания. Также это позволяет получить узлы с улучшенной центральной позицией в рисунке. Это также может повлиять на расстояние между вершинами в одной компоненте связности. Аналоги магнитных полей могут быть использованы для ориентированных графов. Силы отталкивания можно расположить как на ребрах, так и на узлах с целью избежать наложения или почти наложения в конечном рисунке. В рисунках с кривыми ребрами, такими как дуги окружностей или сплайны, силы могут быть также расположены в контрольных точках этих кривых, например, чтобы улучшить угловое разрешение.
Как только силы на узлах и ребрах определены, поведение всего графа под действием этих сил может быть итеративно промоделировано, как если бы это была физическая система. В такой ситуации силы, действующие на узлы, пытаются стянуть их ближе или оттолкнуть их друг от друга подальше. Это продолжается, пока система не придет в состояние механического равновесия, то есть положение узлов не меняется от итерации у итерации. Положения узлов в этом состоянии равновесия используется для генерации рисунка графа.
Для сил, определенных из пружин, идеальная длина которых пропорциональна расстоянию в графе, мажорирование стресса дает очень хорошее поведение (то есть монотонную сходимость) и математически элегантный путь минимизации этой разницы и, следовательно, к хорошему размещению вершин графа.
Можно также использовать механизмы, которые ищут минимум энергии более прямо, а не по физической модели . Такие механизмы, являющиеся примерами общих методов глобальной оптимизации, включают имитацию отжига и генетические алгоритмы .
Следующие свойства являются наиболее важными преимуществами силовых алгоритмов:
Результаты хорошего качества
По меньшей мере для графов среднего размера (до 50-500 вершин), полученные результаты обычно имеют очень хорошие рисунки графов по следующим критериям: однородность длин ребер, равномерное распределение вершин и симметрия. Последний критерий наиболее важен и трудно достижим в других типах алгоритмов.
Гибкость
Силовые алгоритмы могут быть легко приспособлены и расширены для дополнительных эстетических критериев. Это делает алгоритмы более универсальными классами алгоритмов визуализации графов. Примерами существующих расширений являются алгоритмы для ориентированных графов, визуализация трехмерных графов, кластерная визуализация графов, визуализация графов с ограничениями и динамическая визуализация графов.
Интуитивность
Поскольку алгоритмы основаны на физических аналогах привычных объектов, наподобие пружин, поведение алгоритмов относительно просто предсказать и понять. Этого нет в других типах алгоритмов визуализации графов.
Простота
Типичные силовые алгоритмы просты и могут быть реализованы в несколько строк кода. Другие классы алгоритмов визуализации, такие как алгоритмы на основе ортогональных размещений, обычно требует куда больше работы.
Интерактивность
Еще одним преимуществом этого класса алгоритмов является аспект интерактивности. При рисовании промежуточных этапов графа пользователь может проследить как меняется граф, прослеживая эволюцию от беспорядочного месива в хорошо выглядящую конфигурацию. В некоторых средствах интерактивного рисования графа пользователь может отбросить один или несколько узлов из состояния равновесия и наблюдать миграцию узлов в новое состояние равновесия. Это дает алгоритмам преимущество для динамических и онлайновых систем визуализации графов.
Строгая теоретическая поддержка
В то время как простые силовые алгоритмы часто появляются в литературе и на практике (поскольку они относительно просты и понятны), начинает возрастать число более обоснованных подходов. Статистики решали подобные задачи в многомерном шкалировании (англ. multidimensional scaling, MDS) с 1930-х годов, а физики также имеют длинную историю работы со связанными задачами моделирования движения n тел[en], так что существуют вполне вызревшие подходы. Как пример, подход мажорирования стресса к метрическим MDS может быть применен для визуализации графа и в этом случае можно доказать монотонную сходимость. Монотонная сходимость, свойство , что алгоритм будет на каждой итерации уменьшать напряжение или цену размещения вершин, важно, поскольку это гарантирует, что размещение, в конечном счете, достигнет локального минимума и алгоритм остановится. Глушение колебаний приводит к остановке алгоритма, но не гарантирует, что будет достигнут истинный локальный минимум.
Главные недостатки силовых алгоритмов:
Большое время работы
Типичные силовые алгоритмы в общем случае, как считается, имеют время работы, эквивалентные O(n3), где n — число узлов входного графа. Это потому, что число итераций оценивается в O(n), а на каждой итерации необходимо просмотреть все пары узлов и вычислить взаимные силы отталкивания. Это похоже на задачу N-тел в физике. Однако, поскольку силы отталкивания локальны по природе, граф может быть разбит так, что будут рассматриваться только соседние вершины. Основные техники, использованные алгоритмами для определения размещения узлов больших графов, включают вложения высокой размерности , многоуровневые представления и другие методы, связанные с моделированием задачи n тел . Например, основанный на моделировании Барнса-Хата метод FADE может улучшить время работы до n*log(n) на итерацию. В качестве грубой оценки , за несколько секунд можно ожидать рисования максимум 1000 узлов в стандартной технике n2 на итерацию и 100000 с техникой n*log(n) на итерацию . Силовые алгоритмы , когда они комбинируются с многоуровневым подходом, могут рисовать графы с миллионами узлов .
Плохие локальные минимумы
Легко видеть, что силовой алгоритм дает граф с минимальной энергией, в частности, это может быть лишь локальный минимум. Найденный локальный минимум может быть, во многих случаях существенно хуже глобального минимума, что приводит к представлению плохого качества. Для многих алгоритмов, особенно для тех, которые позволяют только движение градиентного спуска, на конечный результат может сильно влиять начальное положение, которое в большинстве случаев генерируется случайно. Проблема плохого локального минимума становится особенно важной при росте числа вершин графа. Комбинирвание различных алгоритмов помогает решить эту проблему . Например, можно использовать алгоритм Камады — Каваи для быстрой генерации приемлемого начального размещения, а затем алгоритм Фрухтермана — Рейнгольда для улучшения положения соседних узлов. Другая техника получения глобального минимума — использование многоуровнего подхода .
Силовые методы визуализации графов восходят к работе Татта в которой он показал, что полиэдральные графы могут быть нарисованы на плоскости с выпуклыми гранями путем фиксации вершин внешней грани планарного вложения графа в выпуклом положении, расположения подобных пружинам притягивающих сил на каждом ребре и позволения системе прийти в равновесное состояние . Ввиду простой природы сил в этом случае система не может застрять в локальном минимуме, а сходится к единственной глобальной оптимальной конфигурации. Ввиду этой статьи вложения планарных графов с выпуклыми гранями иногда назывют вложениями Татта.
Комбинацию сил притяжения смежных вершин графа и сил отталкивания для всех вершин первым использовал Идс . Еще одну пионерскую работу по этому типу силового размещения опубликовали Фрухтерман и Рейнгольд. Идея использования лишь сил пружин между всеми парами вершин с идеальными длинами пружин, равными расстоянию по графу, принадлежит Камаде и Каваи
Существуют библиотеки для визуализации графов на JS, Java, PHP, SQL
Non-SQL для работы с графами в том числе с визуализацией
вот пример такой БД
http://console.neo4j.org/
https:// neo4j .com/
Визуализация гибкого force-directed графа осуществляется с использованием метода численного интегрирования Верле библиотека JS https://github.com/d3/d3
библиотека https://www.graphviz.org/
и другие
Исследование, описанное в статье про визуализация графов, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое визуализация графов, силовые алгоритмы визуализации графов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.