Лекция
Привет, сегодня поговорим про числовые характеристики графов, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое числовые характеристики графов, хроматическое число графов, хроматическое число, реберная раскраска, хроматический многочлен , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
хроматическое число графа G — минимальное число цветов, в которые можно раскрасить вершины графа G так, чтобы концы любого ребра имели разные цвета. Обозначается χ(G).
Хроматическое число графа — минимальное число  , такое что множество
, такое что множество  вершин графа можно разбить на
вершин графа можно разбить на  непересекающихся классов
непересекающихся классов 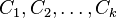 :
:

таких, что вершины в каждом классе независимы, то есть любое ребро графа не соединяет вершины одного и того же класса.
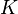 . То есть его вершины можно раскрасить
. То есть его вершины можно раскрасить 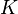 разными цветами так, что у любого ребра концы будут разного цвета.
разными цветами так, что у любого ребра концы будут разного цвета.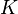 . То есть вершины графа можно раскрасить
. То есть вершины графа можно раскрасить 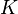 цветами так, что у любого ребра концы будут разного цвета, но так раскрасить
цветами так, что у любого ребра концы будут разного цвета, но так раскрасить 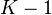 цветами — уже нельзя.
цветами — уже нельзя.
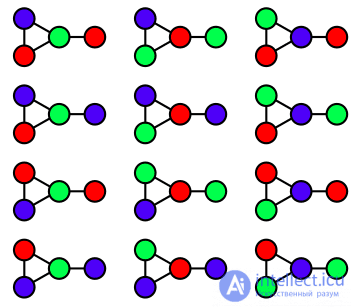
Этот граф может быть раскрашен 3 цветами 12 способами.
Когда говорят о раскраске графов, почти всегда подразумевают под этим раскраску их вершин, то есть присвоение цветовых меток вершинам графа так, чтобы любые две вершины, имеющие общее ребро, имели разные цвета. Так как графы, в которых есть петли, не могут быть раскрашены таким образом, они не являются предметом обсуждения.
Терминология, в которой метки называются цветами, происходит от раскраски политических карт. Такие метки как красный или синий используются, только когда число цветов мало, обычно же подразумевается, что метки являются целыми числами .
Раскраска с использованием цветов называется
-раскраской. Наименьшее число цветов, необходимое для раскраски графа
, называется его хроматическим числом и часто записывается как
. Иногда используется
, с тех пор как
обозначает Эйлерову характеристику. Подмножество вершин, выделенных одним цветом, называется цветовым классом, каждый такой класс формирует независимый набор. Таким образом,
-раскраска — это то же самое, что и разделение вершин на {\displaystyle k}
независимых наборов[1].

Корректная раскраска вершин графа Петерсена наименьшим набором цветов — тремя.
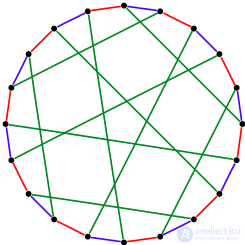
реберная раскраска кубического графа Дезарга.
Хроматический класс графа G — минимальное число цветов, в которые можно раскрасить ребра графа G так, чтобы смежные ребра имели разные цвета. Об этом говорит сайт https://intellect.icu . Обозначается χ'(G). Проблема реберной раскраски произвольного плоского кубического графа без мостов тремя цветами эквивалентна знаменитой Проблеме четырех красок. Реберная раскраска определяет 1-факторизацию графа.
Если рассмотреть количество различных раскрасок помеченного графа как функцию от доступного числа цветов t, то оказывается, что эта функция всегда будет полиномом от t. Этот факт был обнаруженБиркгофом и Льюисом [1] при попытке доказать гипотезу четырех красок.
Треугольник  |
 |
Полный граф  |
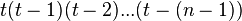 |
Дерево с 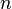 вершинами вершинами |
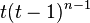 |
Цикл  |
 |
| Граф Петерсена |  |
Для графа-вершины хроматический многочлен равен 
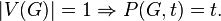
Хроматический многочлен графа равен произведению хроматических многочленов его компонент

Также существует рекуррентное соотношение
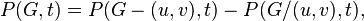
где 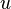 и
и  — смежные вершины,
— смежные вершины, 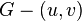 — граф, получающийся из графа
— граф, получающийся из графа 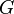 путем удаления ребра
путем удаления ребра 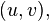 а
а 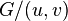 — граф, получающийся из графа
— граф, получающийся из графа 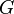 путем стягивания ребра
путем стягивания ребра 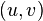 в точку.
в точку.
Можно использовать эквивалентную формулу

где 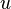 и
и  — несмежные вершины, а
— несмежные вершины, а 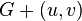 — граф, получающийся из графа
— граф, получающийся из графа 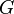 путем добавления ребра
путем добавления ребра 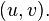
Для всех целых положительных 
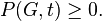
Хроматическое число 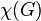 — наименьшее целое положительное
— наименьшее целое положительное  , для которого
, для которого
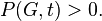
Также хроматическое число можно рассматривать для других объектов, например, для метрических пространств. Так, хроматическим числом плоскости называется минимальное число цветов χ, для которого существует такая раскраска всех точек плоскости в один из цветов, что никакие две точки одного цвета не находятся на расстоянии ровно 1 друг от друга. Аналогично для любой размерности пространства. Элементарно доказывается, что для плоскости  , однако продвинуться дальше до сих пор не удается. Эта задача называется проблемой Нелсона — Эрдеша — Хадвигера.
, однако продвинуться дальше до сих пор не удается. Эта задача называется проблемой Нелсона — Эрдеша — Хадвигера.
Множество глубоких задач теории графов легко формулируются в терминах раскраски. Самая знаменитая из таких задач, проблема четырех красок, в настоящее время решена, однако появляются новые, например, обобщение проблемы четырех красок, гипотеза Хадвигера.
Раскраска вершин моделирует многие проблемы планирования. В своей простейшей постановке заданный набор работ должен быть распределен по временным отрезкам, каждая такая работа занимает один отрезок. Они могут быть выполнены в любом порядке, но две работы могут конфликтовать в том смысле, что не могут быть выполнены одновременно, так как, например, используют общие ресурсы. Соответствующий граф содержит вершину для каждой из работ и ребро для каждой конфликтующий пары. Хроматическое число построенного графа — это минимальное время выполнения всех работ без конфликтов.
Детали проблемы планирования определяют структуру графа. Например, когда идет распределение самолетов по рейсам, результирующий граф конфликтов является интервальным графом, так что проблема раскраски может быть решена эффективно. При распределении радиочастот получается граф единичных кругов конфликтов, и для такой задачи существует 3-аппроксимационный алгоритм.
Компилятор — это компьютерная программа, которая переводит один компьютерный язык в другой. Для улучшения времени выполнения результирующего кода одной из техник компиляторной оптимизации, является распределение регистров, в которой наиболее часто используемые переменные компилируемой программы хранятся в быстродействующих регистрах процессора. В идеальном случае переменные хранятся в регистрах так, что они все находятся в регистрах во время их использования.
Стандартный подход к этой задаче состоит в сведении ее к задаче раскраски графов[8]. Компилятор строит интерференционный граф, где вершины соответствуют переменным, а грань соединяет две из них, если они нужны в один и тот же момент времени. Если этот граф k-хроматический, то переменные могут храниться в k регистрах.
Технология цифровых водяных знаков (англ. digital watermarking) позволяет вместе с данными (будь то медиафайлы, исполняемые файлы и прочие) передать некое скрытое сообщение («водяной знак», Watermark). Такое скрытое сообщение может быть применено в защите авторских прав для идентификации владельца данных.
Это важно, например, для установления источника их распространения нелегальным образом. Или же для подтверждения прав на данные, например — программное обеспечение систем на кристалле (system-on-chip).
Сообщение можно закодировать в том числе и в способе распределения регистров. Одну из таких техник предложили Qu и Potkonjak[37] (поэтому ее иногда называют QP-алгоритмом).
Состоит она вот в чем: пусть — граф несовместимости (интерференционный граф) распределения регистров процессора, о котором говорилось выше. Его раскраска используется в программе — причем, используется так, что допустимо поменять содержимое графа с небольшим увеличением его хроматического числа. Оказывается возможно закодировать послание в программном продукте с помощью раскраски графа
, то есть распределения регистров.
Извлечь это сообщение можно путем сравнением распределения регистров с исходной раскраской;[38] существуют и способы удостовериться в том, было ли некое сообщение закодировано в программе без использования исходного.
В дальнейшем разные авторы развивали и уточняли идеи Qu и Potkonjak[39].[38][40]
Задача раскраски графов была поставлена во многих других областях применения, включая сопоставление с образцом.
Решение головоломки судоку можно рассматривать как завершение раскраски 9 цветами заданного графа из 81 вершины.
На этом все! Теперь вы знаете все про числовые характеристики графов, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое числовые характеристики графов, хроматическое число графов, хроматическое число, реберная раскраска, хроматический многочлен и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Из статьи мы узнали кратко, но содержательно про числовые характеристики графов
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.