Число внутренней устойчивости графа кратко

Привет, сегодня поговорим про число внутренней устойчивости графа, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое число внутренней устойчивости графа , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

Число внутренней устойчивости (= число независимости, = число неплотности) графа 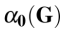– это максимальное количество вершин в графе, не смежных между собой.

Множество SМX называется внутренне устойчивым в графе (Х,Г), если никакие две его вершины не смежны. Число a(G) = 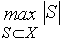называется числом внутренней устойчивости.

Рис.10

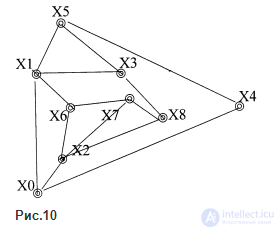
Например, для симметричного графа на рис.10 можно построить несколько максимальных внутренне устойчивых множеств (например, {X₀X₅X₆X₈}) и a(G) = 4.

Примерами его поиска служат задача непоражающего размещения 8 ферзей на шахматной доске (симметричный граф с 64 вершинами; 92 решения - 76 были найдены Гауссом) (рис.11) задача о 15 девушках, которых можно водить на прогулку тройками, в которые каждая пара попадает не более одного раза, - a(G) = 35 при C³₁₅ = 455 тройках

Можно показать, что a(G) Ч g(G)і|Х|; a(GґH) і a(G)Ч a(H).

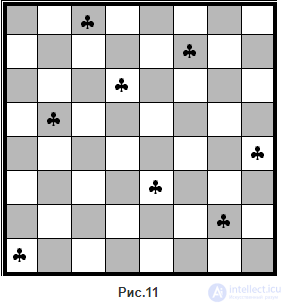Рис.11	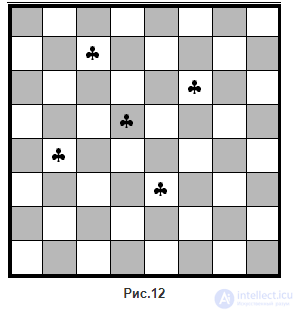Рис.12

Аппарат внутренней устойчивости, в частности, используется при решении задачи помехозащищенной передачи сигналов (задача Шеннона об информационной емкости множества сигналов ).

См. Об этом говорит сайт https://intellect.icu . также

• Устойчивость графа
• Внешняя устойчивость орграфа
• граф ма тика ,
• теория графов , графы , граф ,
• число внешней устойчивости графа , множество внешней устойчивости ,
• экстремальное число графа

Надеюсь, эта статья про число внутренней устойчивости графа, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое число внутренней устойчивости графа и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.