Привет, сегодня поговорим про перестановки, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое перестановки, сочетания, размещения, перестановки с повторениями , перестановки без повторений, соединения в комбинаторике , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

Таблица Отличие и признаки сочетаний, размещений и перестановок

Признаки
	перестановки	сочетания	размещения
Порядок следования элементов	+	–	+
Состав элементов	–	+	+

Сводка формул для всех видов соединений в комбинаторике

Перестановка виды в комбинаторике

6 перестановок 3-х шаров

В комбинаторике перестановка — это упорядоченный набор чисел 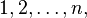обычно трактуемый как биекция на множестве , которая числу i ставит в соответствие i-й элемент из набора. Число n при этом называется порядком перестановки. Как синоним слову "перестановка" в этом смысле некоторые авторы используют слово расстановка.

В теории групп под перестановкой произвольного множества подразумевается биекция этого множества на себя. Как синоним слову "перестановка" в этом смысле некоторые авторы используют слово подстановка. (Другие авторы подстановкой называют наглядный способ записи перестановки.)

Свойства перестановок

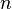• Число всех перестановок порядка равно числу размещений из n по n, то есть факториалу:[

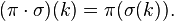• Композиция определяет операцию произведения на перестановках одного порядка: Относительно этой операции множество перестановок порядка n образует группу, которую называют симметрической и обычно обозначают .
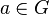• Любая группа является подгруппой группы перестановок множества элементов этой группы (теорема Кэли). При этом каждый элемент сопоставляется с перестановкой 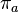, задаваемой тождеством где g — произвольный элемент группы G, а — групповая операция.

Связанные определения

• Носитель перестановки — это подмножество множества 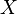, определяемое как
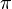• Неподвижной точкой перестановки является всякая неподвижная точка отображения , то есть элемент множества 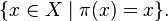Множество всех неподвижных точек перестановки 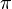является дополнением ее носителя в .
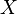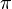• Инверсией в перестановке порядка n называется всякая пара индексов 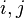такая, что 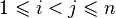и 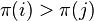. Четность числа инверсий в перестановке определяет четность перестановки.

Специальные типы перестановок

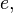• Тождественная перестановка — перестановка которая каждый элемент отображает в себя:
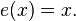
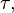• Инволюция — перестановка которая является обратной самой себе, то есть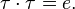
• Беспорядок — перестановка без неподвижных точек.
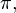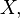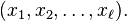• Циклом длины называется такая подстановка которая тождественна на всем множестве кроме подмножества и Обозначается . Число перестановок, содержащих k циклов, - есть числа Стирлинга первого рода
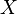• Транспозиция — перестановка элементов множества , которая меняет местами два элемента. Транспозиция является циклом длины 2.

Подстановка

Перестановка 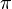множества 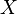может быть записана в виде подстановки, например:

где 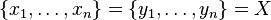и

Произведения циклов и знак перестановки[править ]

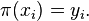
Любая перестановка 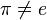может быть разложена в произведение (композицию) непересекающихся циклов длины 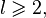причем единственным образом с точностью до порядка следования циклов в произведении. Например:

Любой цикл может быть разложен в произведение (не обязательно непересекающихся) транспозиций. Для произвольного цикла длины 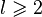разложение можно написать так: Циклы длины 1 действуют как тождественная перестановка и тоже могут быть легко разложены, так как квадрат любой транспозиции есть тождественная перестановка: 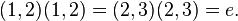Такое разложение циклов на произведение транспозиций не будет единственным: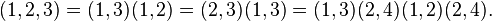

Таким образом любая перестановка может быть разложена в произведение транспозиций. Об этом говорит сайт https://intellect.icu . Хотя это разложение и не будет единственным, но четность числа транспозиций, входящих в разложение, сохраняется. 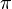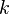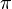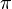Пусть перестановка разложена в произведение транспозиций, тогда знаком перестановки (иначе:четностью перестановки или сигнатурой перестановки) называют число при этом называют четной перестановкой, если 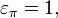инечетной перестановкой, если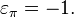

Знак перестановки 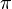также может быть определен через число инверсий 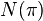в этой перестановке: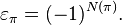

Замечание. Имеется два соглашения по умножению перестановок и циклов:

1) .

Например: .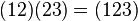

2) .

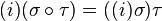Например: .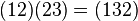

Перестановки с повторением в комбинаторике

Рассмотрим n элементов m различных типов, причем в каждом типе все элементы одинаковы. Тогда перестановки из всех этих элементов с точностью до порядка следования однотипных элементов называются перестановками с повторением. Если ki — количество элементов i-го типа, то 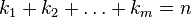и количество всевозможных перестановок с повторениями равно мультиномиальному коэффициенту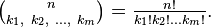

Случайная перестановка

Обобщенная схема размещения

Случайной перестановкой называется случайный вектор 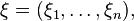все элементы которого принимают натуральные значения от 1 до 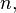и при этом вероятность совпадения любых двух элементов равна 0.

Независимой случайной перестановкой называется такая случайная перестановка , для которой

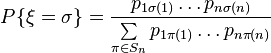
для некоторых 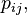таких что

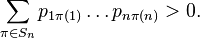
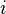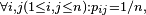Если при этом не зависят от , то перестановку называют одинаково распределенной. Если же нет зависимости от , то есть то называют однородной.

Размещение в комбинаторике. Виды

В комбинаторике размещением (из n по k) называется упорядоченный набор из k различных элементов из некоторого множества различных n элементов.

Пример 1: 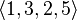— это 4-элементное размещение из 6-элементного множества .

Пример 2: некоторые размещения элементов множества по 2: … … …

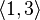
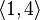
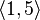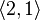
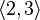
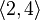В отличие от сочетаний, размещения учитывают порядок следования предметов. Так, например, наборы и являются различными, хотя состоят из одних и тех же элементов 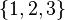(то есть совпадают как сочетания).

Пример

• В фирме работают 8 человек одинаковой квалификации, среди них Иванов, Петров, Сидоров. Сколькими способами можно случайно выбрать
трех из восьми?

Решение

• Всего вариантов - выбрать три из восьми без повторения, т.к. один и тот же не может выполнять две работы

Количество размещений

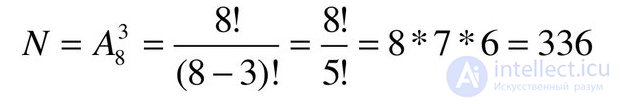
Количество размещений из n по k, обозначаемое 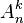, равно убывающему факториалу:

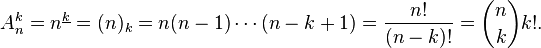
Последнее выражение имеет естественную комбинаторную интерпретацию: каждое размещение из n по k однозначно соответствует некоторому сочетанию из nпо k и некоторой перестановке элементов этого сочетания; число сочетаний из n по k равно биномиальному коэффициенту 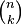, в то время как перестановок наk элементах ровно k! штук.

При k=n количество размещений равно количеству перестановок порядка n:

Размещение с повторениями

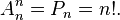
Размещение с повторениями или выборка с возвращением — это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз.

Пример задач

Замок камеры хранения имеет четыре диска, каждый из которых разделен на 10 секторов; насекторах каждого из дисков написаны цифры 0, 1, …, 9.
• Какова вероятность открыть закрытую камеру для человека:
1. забывшего все, что он набрал на дисках, закрывая камеру;
2. помнящего только цифру, набранную на первом диске;
3. помнящего только, что ни на втором, ни на третьем, ни на четвертом, диске не набирал цифру 6?

. Решение

3) Всего вариантов N=10*9*9*9

Количество размещений с повторениями

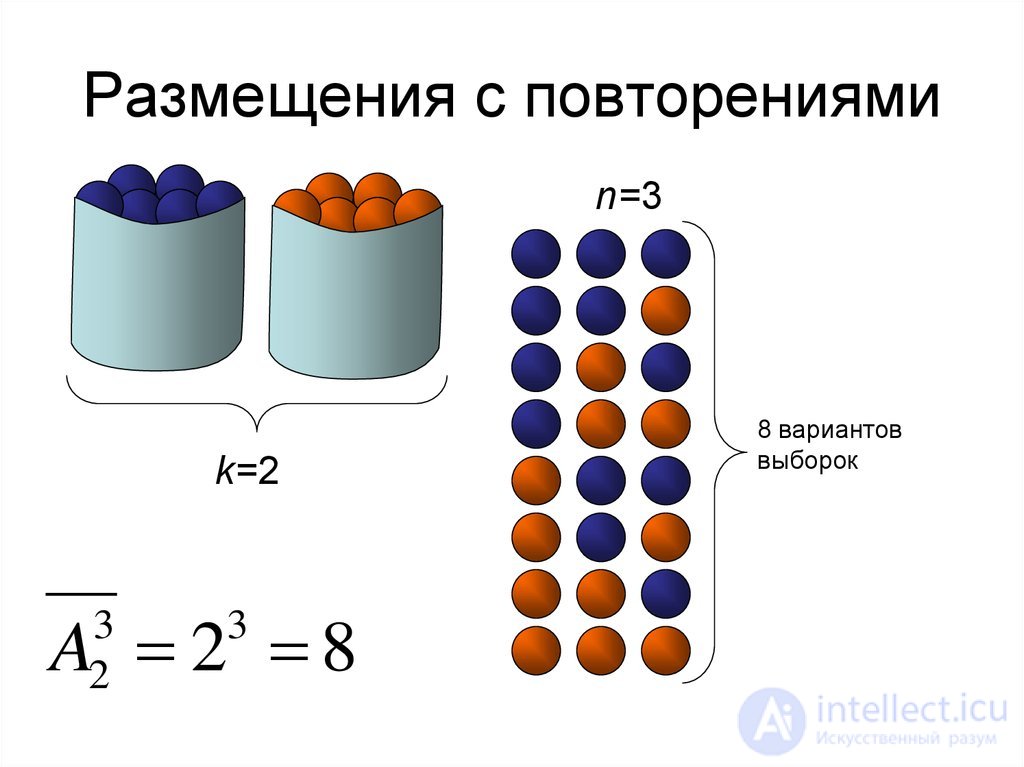
По правилу умножения количество размещений с повторениями из n по k, обозначаемое 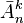, равно:

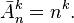
Например, количество вариантов 3-значного кода, в котором каждый знак является цифрой от 0 до 9 и может повторяться, равно:

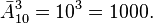
Еще один пример: размещений с повторениями из 4 элементов a, b, c, d по 2 равно 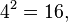эти размещения следующие:

Сочетание в комбинаторике. Виды

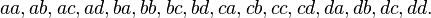
В комбинаторике сочетанием из 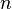по 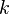называется набор 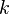элементов, выбранных из данного множества, содержащего 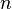различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.

Так, например, наборы (3-элементные сочетания, подмножества, 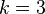) {2, 1, 3} и {3, 2, 1} 6-элементного множества {1, 2, 3, 4, 5, 6} (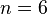) являются одинаковыми (в то время как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.

В общем случае число, показывающее, сколькими способами можно выбрать 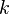элементов из множества, содержащего 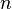различных элементов, стоит на пересечении 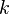-й диагонали и 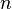-й строки треугольника Паскаля.

Пример

В чемпионате по шахматам участвовало 40 спортсменов. Каждый с каждым сыграл по одной партии. Сколько всего партий было сыграно?

Число сочетаний

Биномиальный коэффициент

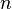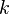Число сочетаний из по равно биномиальному коэффициенту

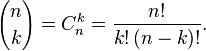
При фиксированном 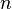производящей функцией последовательности чисел сочетаний , , 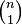, … является:

Двумерной производящей функцией чисел сочетаний является

Сочетания с повторениями

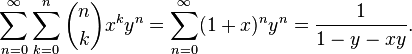
Сочетанием с повторениями называются наборы, в которых каждый элемент может участвовать несколько раз.

Число сочетаний с повторениями из 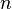по 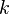равно биномиальному коэффициенту

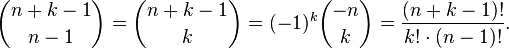
Доказательство

Пусть имеется 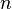типов объектов, причем объекты одного типа неотличимы. Пусть имеется неограниченное (или достаточно большое, во всяком случае, не меньше 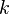) количество объектов каждого типа. Из этого ассортимента выберем 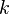объектов; в выборке могут встречаться объекты одного типа, порядок выбора не имеет значения. Обозначим через количество выбранных объектов -го типа, 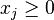, 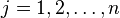. Тогда . Но число решений этого уравнения легко подсчитывается с помощью «шаров и перегородок»: каждое решение соответствует расстановке в ряд 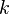шаров и 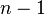перегородок так, чтобы между 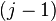-й и -й перегородками находилось ровно шаров. Но таких расстановок в точности 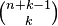, что и требовалось доказать.

При фиксированном 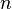производящей функцией чисел сочетаний с повторениями из 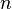по 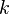является:

Двумерной производящей функцией чисел сочетаний с повторениями является:

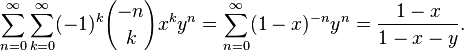
Пример Имеется 2 типа цветов, количество цветов не ограничено. Сколько различных букетов можно составить из 3-х цветов?
• 111
• 222
• 122
• 211
• Всего 4 различных букета

Пример Имеется 5 типов цветов, количество цветов не ограничено. Сколько различных букетов можно составить из 3-х цветов?

Решение

• Сочетание с повторением:
(5+3-1)!/(3!*(5-1) !)=35

Какое отличие сочетания с повторениями от размещения с повторениями?

Сочетания с повторениями и размещения с повторениями — это два разных математических понятия, и их отличие заключается в том, как элементы выбираются и упорядочиваются при формировании комбинаций.

1. Сочетания с повторениями:

   • В сочетаниях с повторениями элементы выбираются из некоторого набора так, что один и тот же элемент может быть выбран несколько раз. Важно знать только, какие элементы были выбраны и сколько раз, но не в каком порядке они были выбраны.
   • Формула для сочетаний с повторениями C(n + r - 1, r), где n - количество элементов в наборе, r - количество элементов, выбираемых с повторениями.

   Пример: Выбор комбинации блюд в меню ресторана, где вы можете выбирать одно и то то же блюдо несколько раз.

2. Размещения с повторениями:

   • В размещениях с повторениями элементы также выбираются из некоторого набора, но порядок выбора имеет значение. То есть, один и тот же элемент может встречаться несколько раз, но его позиция в комбинации имеет значение.
   • Формула для размещений с повторениями A(n, r) = n^r, где n - количество элементов в наборе, r - количество элементов, выбираемых с повторениями.

   Пример: Создание паролей для учетных записей, где символы (буквы, цифры и символы) могут повторяться, и порядок символов важен.

Важное отличие между сочетаниями с повторениями и размещениями с повторениями заключается в том, как учитывается порядок выбранных элементов. В сочетаниях с повторениями порядок не имеет значения, а в размещениях с повторениями порядок имеет значение.

Примеры из жизни- Перестановок, размещений, сочетаний без повторений и с повторениями

1. перестановки без повторений :

   Пример: Вы хотите узнать, сколько различных способов можно расставить 5 книг на полке. В данном случае, порядок, в котором книги стоят на полке, имеет значение, и вы не можете использовать одну и ту же книгу несколько раз. Переставить 5 книг на полке можно 5! (5 факториал) различными способами.

2. Размещения без повторений:

   Пример: Вам нужно выбрать 2 сотрудника для представления вашей компании на выставке. Важно, кто будет выступать первым, а кто вторым. В этом случае, порядок имеет значение, и вы не можете выбрать одного и того же сотрудника дважды. Количество размещений будет равно 2P2 = 2 способа (первый сотрудник идет первым, второй - вторым, и наоборот).

3. Сочетания без повторений:

   Пример: Вам нужно выбрать команду из 3 игроков для участия в баскетбольном турнире. Порядок, в котором игроки были выбраны, не имеет значения, и вы не можете выбрать одного и того же игрока несколько раз. В этом случае количество сочетаний будет равно C(3, 3) = 1 способ (потому что вы выбираете всю команду).

4. Сочетания с повторениями:

   Пример: Вы организуете вечеринку и выбираете напитки для предложения гостям. У вас есть 3 вида напитков: кола, сок и вода. Вы хотите выбрать 2 напитка. В этом случае, порядок не имеет значения, и вы можете выбрать один и тот же вид напитка несколько раз. Количество сочетаний с повторениями будет равно C(3 + 2 - 1, 2) = C(4, 2) = 6 способов (кола и сок, кола и вода, сок и вода, и так далее).

5. перестановки с повторениями : Пример: У вас есть слово "ААББ". Сколько существует различных способов переставить буквы в этом слове? Поскольку есть повторяющиеся буквы, вы не можете рассматривать каждую букву как уникальную. Количество перестановок равно 4! / (2! * 2!) = 6 способов. Это потому, что "А" повторяется дважды и "Б" также повторяется дважды. Пример: Вы готовите салат из 3 помидоров, 2 огурцов и 1 моркови. Сколько различных способов можно пересортировать эти овощи на тарелке? Поскольку у вас есть повторяющиеся овощи, количество перестановок равно 6! / (3! * 2!) = 60 способов.

6. Размещения с повторениями: Пример: Вам нужно выбрать команду из 4 игроков для игры в футбол. Однако, вы хотите, чтобы каждый игрок имел определенную роль: вратарь, защитник, полузащитник и нападающий. Сколько различных способов выбора игроков и их ролей? В этом случае, размещения с повторениями подходят, и ответ будет равен 4^4 = 256 способов, так как для каждой из 4 ролей есть 4 игрока для выбора. Пример: Вы создаете пароль из 4 символов, и каждый символ может быть заглавной латинской буквой (A-Z) или цифрой (0-9). Сколько различных паролей можно создать? Здесь также используются размещения с повторениями, и ответ равен 36^4 = 1,679,616 различных паролей (потому что есть 36 возможных символов для каждой из 4 позиций).

если знаешь еще реальные примеры из повседнейной жизни пиши в комментах

Открыть на весь экран

Вау!! 😲 Ты еще не читал? Это зря!

• перестановки , сочетания , размещения , бином ньютона ,
• сводка формул для всех видов соединений , комбинаторика , перестановки , размещения с повторениями ,

На этом все! Теперь вы знаете все про перестановки, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое перестановки, сочетания, размещения, перестановки с повторениями , перестановки без повторений, соединения в комбинаторике и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.