Гиперграф

Привет, сегодня поговорим про гиперграф, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое гиперграф , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

Пример гиперграф а: ,   .

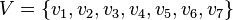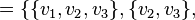
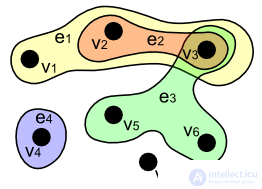
Гипергра́ф — обобщение графа, в котором каждым ребром могут соединяться не только две вершины, но и любые подмножества вершин.

С математической точки зрения, гиперграф представляет собой пару , где 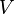 — непустое множество объектов некоторой природы, называемых вершинами гиперграфа, а  — семейство непустых (необязательно различных) подмножеств множества 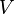, называемых ребрами гиперграфа.

Гиперграфы применяются, в частности, при моделировании электрических цепей.

Трансверсалью гиперграфа является множество , содержащее непустое пересечение с каждым ребром. Об этом говорит сайт https://intellect.icu . Такая трансверсаль будет минимальной, если никакое ее подмножество само не является трансверсалью гиперграфа.

Литература[править ]

• В. А. Емеличев, О. И. Мельников, В. И. Сарванов, Р. И. Тышкевич Глава XI: Гиперграфы // Лекции по теории графов. —М.: Наука, 1990. — С. 298—315. — 384 с. — ISBN 5-02-013992-0.
• И. А. Головинский Методы анализа топологии коммутационных схем электрических сетей // Электричество. — 2005. — № № 3. — С. 10—18.
• В. А. Евстигнеев, В. Н. Касьянов Толковый словарь по теории графов. — Новосибирск: Наука, 1999.
• А. А. Зыков Гиперграфы // Успехи математических наук. — 1974. — № 6 (180).
• Курейчик В.М., Глушань В.М., Щербаков Л.И. Комбинаторные аппаратные модели и алгоритмы в САПР. М.: Радио и связь, 1990. 216 с.

На этом все! Теперь вы знаете все про гиперграф, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое гиперграф и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.