Лекция
Привет, Вы узнаете о том , что такое стягивание ребра, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое стягивание ребра, отождествление вершин , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
В теории графов стягивание ребра — это операция, которая удаляет ребро из графа, а до этого связанные ребром вершины сливаются в одну вершину. Стягивание ребра является фундаментальной операцией в теории о минорах графов. отождествление вершин — другая форма этой операции с более слабыми ограничениями.
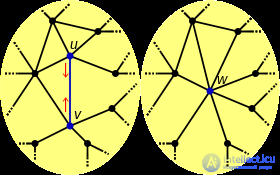
Операция стягивания ребра производится над конкретным ребром e. Ребро e удаляется, а две его инцидентные вершины, u и v, сливаются в новую вершину w, где ребра, инцидентные w, соответствуют ребрам, инцидентным либо u, либо v. Более обще, операция может быть проведена на множестве ребер путем стягивания ребер из множества (в любом порядке) .
Как определено ниже, операция стягивания ребра может дать граф с кратными ребрами даже если исходный граф был простым графом . Однако некоторые авторы не разрешают создание кратных ребер, так что стягивание ребер на простом графе всегда дают простые графы.
Пусть G=(V,E) — граф (или ориентированный граф), содержащий ребро e=(u,v) с u≠v. Об этом говорит сайт https://intellect.icu . Пусть f — функция, которая отображает любую вершину в V в себя, а в противном случае — в вершину w. Стягивание e приводит к новому графу G′=(V′,E′), где V′=(V)∪{w}, E′=E, и для любой вершины x∈V, вершина x′=f(x)∈V′ инцидентна ребру e′∈E′ тогда и только тогда, когда соответствующее ребро e∈E инцидентно x в G.
Отождествление вершин (иногда называется стягиванием вершин) не используется ограничение, что стягивание должно проводиться с вершинами, инцидентными одному ребру (таким образом, стягивание ребра является частным случаем отождествления вершин). Эта операция может быть проведена с любой парой (или подмножеством) вершин в графе. Ребра между двумя стягиваемыми вершинами иногда удаляются. Если v и v' — вершины различных компонент графа G, то мы можем создать новый граф G' путем отождествления v и v' в G в новую вершину v в G' .
Расщепление вершин означает замену одной вершины на две, и эти две новые вершины смежны вершинам, которым была смежна исходная вершина. Операция является обратной отождествлению вершин.
Стягивание пути производится с множеством ребер в пути, которые стягиваются, образуя одно ребро между конечными вершинами пути. Ребра, инцидентные вершинам вдоль пути, либо исключаются, либо случайным образом (или по некой системе) соединяются с одной из конечных точек.
Если даны два непересекающихся графа G1 and G2, где G1 содержит вершины u1 и v1, а G2 содержит вершины u2 и v2. Предположим, что мы получили граф G путем отождествления вершин u1 графа G1 и u2 графа G2, получая вершину u в G, и отождествления вершин v1 графа G1 и v2 графа G2, получая вершину v в G. В скручивании G' графа G относительно пары вершин {u, v}, мы отождествляем вместо указанных выше вершины u1 с v2 и v1 с u2 .
Как стягивание ребра, так и стягивание вершин имеют важное значение для доказательства по математической индукции по числу вершин или ребер графа, где можно предположить, что свойство выполняется для всех меньших графов и это может быть использовано для доказательства свойств больших графов.
Стягивание ребра используется в рекурсивной формуле числа стягивающих деревьев случайного связного графа и в рекуррентной формуле для хроматического полинома простого графа .
Стягивание также полезно в структурах, где мы желаем упростить граф путем отождествления вершин, которые представляют существенно эквивалентные объекты. Наиболее известным примером является сведение общего ориентированного графа к ориентированному ациклическому графу стягиванием всех вершин в каждой компоненте сильной связности. Если отношение, описываемое графом является транзитивным, никакая информация не теряется, если пометить каждую вершину множеством меток вершин, которые были стянуты в данную вершину.
Другой пример — слияние, проводимое в раскраске графа при глобальном распределении регистров, где вершины сливаются (где можно) для исключения операций перемещения данных между различными переменными.
Стягивание ребра используется в пакетах трехмерного моделирования (либо вручную, либо с помощью моделирующих программ) для последовательного сокращения числа вершин с целью создания моделей в виде многоугольников с малым числом сторон.
Исследование, описанное в статье про стягивание ребра, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое стягивание ребра, отождествление вершин и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Из статьи мы узнали кратко, но содержательно про стягивание ребра
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.