Теория конечных и бесконечных множеств

Сразу хочу сказать, что здесь никакой воды про конечные множества, и только нужная информация. Для того чтобы лучше понимать что такое конечные множества, бесконечные множества , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

Определение. Множество называется конечным, если оно содержит конечное число элементов и бесконечным, если оно содержит неограниченное число элементов.

Пример. Множество A={1,2,3,4,5,6,7,8,9,0} цифр в десятичной системе счисления конечно, а множество точек окружности бесконечно.

Для сравнения множеств между собой вводят понятие мощности множества. Для конечных множеств понятие мощности соответствует числу элементов множества. Бес конечные множества можно сравнивать по мощности путем установления взаимнооднозначного соответствия между элементами одного и другого множества.

Два множества M и N, называются эквивалентными по мощности (обозначение M ~ N), если между их элементами можно установить биекцию.

Множество называется счетным, если оно эквивалентно множеству натуральных чисел.

Конечное множество

Конечное множество — множество, количество элементов которого конечно, то есть, существует неотрицательное целое число k, равное количеству элементов этого множества. В противном случае множество называется бесконечным. Например,

конечное множество из пяти элементов. Число элементов конечного множества является натуральным числом и называется мощностью множества. Множество натуральных чисел бесконечно:

Конечные множества играют особую роль в комбинаторике, которая изучает дискретные объекты. Рассуждения о конечных множествах используют принцип Дирихле, согласно которому не может существовать инъекция из большего конечного множества в меньшее.

Формальное определение конечного множества

Два множества и называются эквивалентными, если существует биективное отображение одного множества в другое. Если множества X и Y эквивалентны, то этот факт записывают или и говорят, что множества имеют одинаковые мощности.

Множество называется конечным, если оно эквивалентно множеству при некотором неотрицательном целом . При этом число называется количеством элементов множества , что записывается как .

В частности, пустое множество является конечным множеством, количество элементов которого равно 0, то есть, .

Существуют и другие определения конечного множества:

• множество конечно, если оно индуктивно;
• множество конечно, если множество всех его подмножеств нерефлексивно ;
• множество конечно, если оно нерефлексивно;
• множество конечно, если оно не является объединением двух непересекающихся множеств, каждое из которых эквивалентно данному множеству .

Проблема определения конечности множеств в общем случае неразрешима (теорема Трахтенброта). Не существует ни самого слабого, ни самого сильного определения конечного множества. Для каждой логической формулы, являющейся определением конечного множества, существует более сильная и более слабая формулы. Существует неограниченное число логических формул, определяющих конечные множества, и среди них неограниченное множество независимых определений.

Свойства конечного множества

• Регулярное множество не эквивалентно никакому своему собственному подмножеству;
• Если конечные множества попарно не пересекаются (то есть, ), то

  ;

• Если — конечные множества, то

  ;

• Если — конечное множество, то мощность его булеана равна

  

Подсчет количества элементов в конечных множествах

Если множество A конечно, то через |A| обозначается количество элементов в нем.Используют также обозначение #A, особенно когда A записано при помощи фигурныхскобок. Об этом говорит сайт https://intellect.icu . Формально количество элементов конечного множества можно определить поиндукции:Определение 1. Пустое множество является 0-элементным множеством. Если a ∈A и A \ {a} является n-элементным множеством, то множество A является (n + 1)-элементным.

Определение 2. Множество A называется конечным, если оно является n-элементнымдля некоторого n ∈ N.Нужно доказать, что определение корректно, т.е. не зависит от выбора a.

Утверждение 3. Если a1,a2 ∈ A и A \ {a₁} является n-элементным, то A \ {a₂}тоже является n-элементным.

Доказательство. Будем доказывать утверждение по индукции. В качестве базы возь-мем случай n = 0. В этом случае A \ {a1} пусто, откуда A = {a1}. Поскольку a2 ∈ A,получаем, что a2 = a1. Отсюда A\{a2} = A\{a1} = ∅, то есть A\{a2} тоже 0-элементно.Пусть для n утверждение доказано. Докажем для n + 1. Случай a1 = a2 очевиден,поэтому рассмотрим случай a1 = a2. В таком случае a2 ∈ A \ {a1}. Поскольку A \ {a1}является (n+ 1)-элементным, по предположению индукции получаем, что A\{a1,a2} =(A \{a1}) \{a2} является n-элементным. А поскольку a1 ∈ A \{a2} и (A \{a2}) \{a1} =A \ {a1,a2}, получаем, что множество A \ {a2} тоже является (n + 1)-элементным, чтои требовалось доказать.

Следствие 4. Конечное множество A является n-элементным ровно для одного n.Это число n называется количеством элементов в множестве и обозначается |A|

Утверждение 5. Пусть A и B суть конечные множества. Тогда между ними суще-ствует биекция в том и только том случае, когда |A| = |B|.Доказательство. Будем доказывать утверждение по индукции. Пусть существует би-екция F : A → B и |A| = n. Если n = 0, то A = ∅ и в силу биективности B тожедолжно быть пусто. Иначе элементу B ничего бы не соответствовало. Если n > 0, то Aсодержит некоторый элемент a. В силу биективности ему соответствует некоторый эле-мент b. Тогда A \ {a} является (n − 1)-элементным, а F|_A\{a} является биекцией между A \ {a} и B \ {b}. По предположению индукции |B \ {b}| = n − 1 и потому |B| = n, чтои требовалось.Обратно, пусть |A| = |B| = n. Если n = 0, то A = B = ∅ и единственное отображениеF : ∅ → ∅ является биекцией. Если n > 0, то выберем произвольные a ∈ A и b ∈ B.Тогда |A \ {a}| = |B \ {b}| = n1 и существует биекция F : A \ {a} → B \ {b}. Дополнивее значением F(a) = b, получим биекцию между A и B

Бесконечное множество

Бесконечное мно́жество — множество, не являющееся конечным. Можно дать еще несколько эквивалентных определений бесконечного множества:

• Множество, в котором для любого натурального числа найдется конечное подмножество из элементов.
• Множество, в котором найдется счетное подмножество.
• Множество, в котором найдется подмножество, равномощное некоторому (ненулевому) предельному ординалу.
• Множество, для которого существует биекция с некоторым его собственным подмножеством.

Для любого бесконечного множества существует множество с еще большей мощностью — таким образом, не существует бесконечного множества наибольшей мощности. Мощности бесконечных множеств называются алефами («алеф», א — первая буква еврейского алфавита) и обозначаются где индекс пробегает все порядковые числа. Мощности бесконечных множеств составляют вполне упорядоченный класс — наименьшей мощностью бесконечного множества является (алеф-0, мощность множества натуральных чисел), за ним следуют

Примеры бесконечных множеств

• Множества натуральных чисел целых чисел рациональных чисел действительных чисел комплексных чисел — являются бесконечными множествами.
• Множество функций является бесконечным.
• Упорядоченное бесконечное множество может иметь "концы" (минимальный и максимальный элементы) — например, множество рациональных чисел на отрезке
• Совокупность всех бесконечных подмножеств счетного множества является несчетным бесконечным множеством.

Примеры счетных множеств

Рассмотрим несколько примеров счетных множеств.

1. Множество всех целых чисел. Установим биекцию между множеством всех целых чисел и множеством всех натуральных чисел. Для этого расположим элементы этих множеств друг под другом попарно следующим образом

0	-1	1	-2	2	-3	3	-4	4	.	.	.
1	2	3	4	5	6	7	8	9	.	.	.

Этим самым биекция установлена, значит эквивалентность этих множеств доказана.

2. Множество всех рациональных чисел. Каждое рациональное число записывается однозначно в виде несократимой дроби: α=p/q, q>0. Назовем сумму

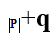высотой рационального числа α. Число дробей с данной высотой конечно. Например, высоту 1 имеет только число 0/1. Высоту 2 - числа 1/1 и -1/1. высоту 3 - числа 2/1, 1/2, -2/1 и -1/2 и т.д. Будем нумеровать все рациональные числа по возрастанию высоты. При этом всякое рациональное число получит некоторый номер, т.е. будет установлена биекция между всеми натуральными и всеми рациональными числами.

Среди всех бесконечных множеств существуют такие, которые не являются счетными - это несчетные множества. Между счетным множеством и несчетным множеством биекцию провести нельзя, в последнем всегда элементов “больше”. Покажем, что множество действительных чисел, заключенных между нулем и единицей, несчетно.

Пусть множество P=[0,1] счетно, т.е. все точки этого отрезка можно последовательно пронумеровать: x₁,x₂,..., x_n,... Разделим отрезок [0,1] на три равных отрезка. Тогда по крайней мере один из отрезков не содержит точки x₁. Точка x₁ может принадлежать либо одному отрезку либо двум, если она лежит на их границе. Отрезок A₁, который не содержит точки x₁, снова разделим на три равных отрезка. По крайней мере один из них A₂ не содержит точки x₂. Отрезок A₂ который не содержит x₂, снова разделим на три равных отрезка и т.д. В результате получим последовательность вложенных один в другой отрезков A₁,A₂,..., A_n. Пусть x_k - точка, которая принадлежит всем этим отрезкам. Тогда, с одной стороны, 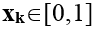и в силу счетности точек отрезка входит в последовательность x₁,x₂,..., x_n,... С другой стороны, точка x_k не может совпасть ни с одной из точек этой последовательности, поскольку отрезки A₁, A_2… так построены, что ни одна из точек счетного множества x₁,x₂,..., x_n,... им не принадлежит. Из этого следует, что принятое допущение о том, что множество P=[0,1]счетное неверно, т.е. множество несчетно.

Несчетные множества тоже можно сравнивать между собой путем построения биекции. Если биекцию удается построить, то этим самым доказывается эквивалентность множеств.

Рассмотрим примеры. Множества точек на любых двух отрезках эквивалентны между собой. На рис.4 показано, как можно установить биекцию между двумя различными отрезками ab и cd.

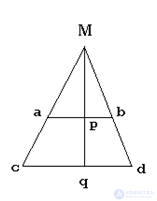
Рис.4. Построение биекции между элементами множеств ab и cd

Множество точек в интервале 0,1 эквивалентно множеству всех точек на прямой. Биекцию можно установить, например, с помощью функции

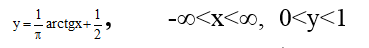
Из приведенных примеров следует, что множество точек любого отрезка эквивалентно множеству точек бесконечной прямой; любые отрезки эквивалентны между собой.

Нетрудно установить из приведенных примеров, что всякое бесконечное множество (счетное и несчетное) эквивалентно своему истинному подмножеству (бесконечному).

Например, натуральных чисел оказывается “столько же” сколько и всех целых, сколько всех четных, нечетных, рациональных и т.д. На любом отрезке можно выделить часть его, а затем построить биекцию между отрезком и его частью, т.е. часть оказывается эквивалентной целому. Это свойство характерно для любого бесконечного множества. Мощность бесконечного множества точек на прямой называется мощностью континуума.

Пусть M - некоторое множество и пусть 2^m - множество - степень M. Тогда 2^m имеет мощность большую, чем мощность исходного множества M. Если рассмотреть множество-степень счетного множества, то оказывается, что его мощность равна мощности континуума. Для любого множества мощности континуума можно рассмотреть его множество-степень и мощность этого нового множества будет больше мощности континуума. Затем можно рассмотреть опять множество-степень этого нового множества и опять его мощность будет больше. Таким образом, не существует верхней границы мощности множеств, подобно тому как не существует “самого большого” числа.

Вау!! 😲 Ты еще не читал? Это зря!

• Бесконечность
• Кардинальное число
• Аксиоматика теории множеств
• Теорема Кантора — Бернштейна
• Континуум
• Континуум - гипотеза
• множество

А как ты думаешь, при улучшении конечные множества, будет лучше нам? Надеюсь, что теперь ты понял что такое конечные множества, бесконечные множества и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.