Лекция
Привет, сегодня поговорим про бинарное отношение, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое бинарное отношение, биекция, сюръекция, инъекция , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
бинарное отношение в математике — двухместное отношение между любыми двумя множествами 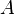 и
и  , то есть всякое подмножество декартова произведения этих множеств:
, то есть всякое подмножество декартова произведения этих множеств:  . Бинарное отношение на множестве
. Бинарное отношение на множестве 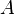 — любое подмножество
— любое подмножество 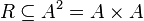 , такие бинарные отношения наиболее часто используются в математике, в частности, таковы равенство, неравенство, эквивалентность, отношение порядка.
, такие бинарные отношения наиболее часто используются в математике, в частности, таковы равенство, неравенство, эквивалентность, отношение порядка.
Бинарным отношением между двумя множествами называется соответствие элементов одного из них элементам второго.
Пусть даны два множества  и
и 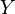 , и пусть
, и пусть 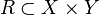 - подмножество их декартова произведения. Тогда тройка
- подмножество их декартова произведения. Тогда тройка 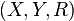 называется бинарным отношением между
называется бинарным отношением между  и
и  Утверждение
Утверждение 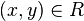 обычно записывается в виде
обычно записывается в виде  и читается "
и читается "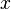 соотносится с
соотносится с  " Если
" Если  то пишут
то пишут 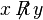 или
или 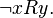
Множество всех первых элементов пар из  называется областью определения отношения
называется областью определения отношения  и обозначается как
и обозначается как 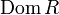 .
.
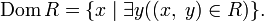
 называется областью значения отношения
называется областью значения отношения  и обозначается как
и обозначается как  .
.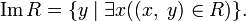
 — это множество
— это множество  и обозначается, как
и обозначается, как 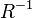 .
. и
и  — это множество
— это множество 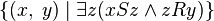 и обозначается, как
и обозначается, как 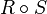 .
.Бинарное отношение  на некотором множестве
на некотором множестве 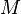 может обладать различными свойствами, например:
может обладать различными свойствами, например:
 ,
, ,
, ,
, ,
,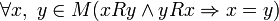 ,
,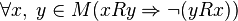 , эквивалентна одновременной антирефлексивности и антисимметричности отношения,
, эквивалентна одновременной антирефлексивности и антисимметричности отношения, ,
,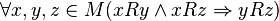 ,
, ,
,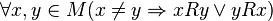 ,
, ,
,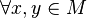 верно ровно одно из трех утверждений:
верно ровно одно из трех утверждений: 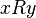 ,
,  или
или 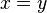 .
.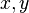 выполняется
выполняется 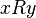 или
или  ) транзитивное отношение называется отношением линейного порядка.
) транзитивное отношение называется отношением линейного порядка. ) — это двухместное отношение, состоящее из пар элементов
) — это двухместное отношение, состоящее из пар элементов 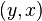 , полученных перестановкой пар элементов
, полученных перестановкой пар элементов 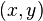 данного отношения
данного отношения  . Обозначается:
. Обозначается: 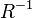 . Для данного отношения и обратного ему верно равенство:
. Для данного отношения и обратного ему верно равенство: 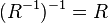 .
. , определенное на некотором множестве и отличающееся тем, что для любого
, определенное на некотором множестве и отличающееся тем, что для любого 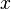 этого множества элемент
этого множества элемент 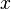 находится в отношении
находится в отношении  к самому себе, то есть для любого элемента
к самому себе, то есть для любого элемента 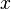 этого множества имеет место
этого множества имеет место 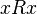 . Примеры рефлексивных отношений: равенство,одновременность, сходство.
. Примеры рефлексивных отношений: равенство,одновременность, сходство. , определенное на некотором множестве и отличающееся тем, что для любого элемента
, определенное на некотором множестве и отличающееся тем, что для любого элемента 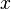 этого множества неверно, что оно находится в отношении
этого множества неверно, что оно находится в отношении  к самому себе (неверно, что
к самому себе (неверно, что 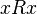 ), то есть возможен случай, что элемент множества не находится в отношении
), то есть возможен случай, что элемент множества не находится в отношении  к самому себе.
к самому себе. , определенное на некотором множестве и отличающееся тем, что для любых
, определенное на некотором множестве и отличающееся тем, что для любых 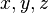 из
из 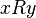 и
и 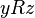 следует
следует 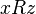 (
(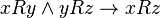 ). Примеры транзитивных отношений: «больше», «меньше», «равно», «подобно», «выше», «севернее».
). Примеры транзитивных отношений: «больше», «меньше», «равно», «подобно», «выше», «севернее». , определенное на некотором множестве и отличающееся тем, что для любых
, определенное на некотором множестве и отличающееся тем, что для любых 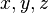 этого множества из
этого множества из 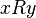 и
и 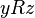 не следует
не следует 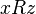 (
( ). Пример нетранзитивного отношения: «x отец y»
). Пример нетранзитивного отношения: «x отец y» , определенное на некотором множестве и отличающееся тем, что для любых элементов
, определенное на некотором множестве и отличающееся тем, что для любых элементов 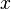 и
и  этого множества из того, что
этого множества из того, что 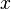 находится к
находится к  в отношении
в отношении  , следует, что и
, следует, что и  находится в том же отношении к
находится в том же отношении к 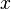 —
— 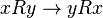 . Примером симметричных отношений могут быть равенство, отношение эквивалентности, подобие, одновременность.
. Примером симметричных отношений могут быть равенство, отношение эквивалентности, подобие, одновременность. , определенное на некотором множестве и отличающееся тем, что для любых
, определенное на некотором множестве и отличающееся тем, что для любых 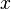 и
и  из
из 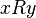 и
и  следует
следует 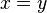 (то есть
(то есть  и
и 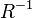 выполняются одновременно лишь для равных между собой членов).
выполняются одновременно лишь для равных между собой членов). , определенное на некотором множестве и отличающееся тем, что для любых
, определенное на некотором множестве и отличающееся тем, что для любых 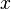 и
и  из
из 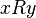 следует
следует 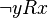 . Пример: отношения «больше» (>) и «меньше» (<).
. Пример: отношения «больше» (>) и «меньше» (<). между объектами
между объектами 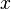 и
и  , являющееся одновременно рефлексивным, симметричным и транзитивным. Примеры: равенство, равномощность двух множеств, подобие, одновременность.
, являющееся одновременно рефлексивным, симметричным и транзитивным. Примеры: равенство, равномощность двух множеств, подобие, одновременность. , определенное на некотором множестве, отличающееся тем, что каждому значению
, определенное на некотором множестве, отличающееся тем, что каждому значению 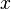 отношения
отношения 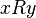 соответствует лишь единственное значение
соответствует лишь единственное значение  . Свойство функциональности отношения
. Свойство функциональности отношения  записывается в виде аксиомы:
записывается в виде аксиомы:  .
. , определенное на некотором множестве, отличающееся тем, что в нем каждому значению
, определенное на некотором множестве, отличающееся тем, что в нем каждому значению 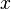 соответствует единственное значение
соответствует единственное значение  , и каждому значению
, и каждому значению  соответствует единственное значение
соответствует единственное значение 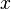 .
. , определенное на некотором множестве, отличающееся тем, что для любых двух различных элементов
, определенное на некотором множестве, отличающееся тем, что для любых двух различных элементов 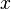 и
и  из этого множества, одно из них находится в отношении
из этого множества, одно из них находится в отношении  к другому (то есть выполнено одно из двух соотношений:
к другому (то есть выполнено одно из двух соотношений: 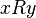 или
или  ). Пример: отношение «меньше» (<).
). Пример: отношение «меньше» (<).Так как отношения, заданные на фиксированной паре множеств 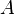 и
и  суть подмножества множества
суть подмножества множества 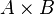 , то совокупность всех этих отношений образует булеву алгебру относительно операций объединения, пересечения и дополнения отношений. В частности, для произвольных
, то совокупность всех этих отношений образует булеву алгебру относительно операций объединения, пересечения и дополнения отношений. В частности, для произвольных 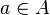 ,
,  :
:
 ,
,
 ,
,
 .
.
Часто вместо объединения, пересечения и дополнения отношений говорят об их дизъюнкции, конъюнкции и отрицании.
Например, 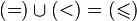 ,
, 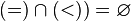 , то есть объединение отношения строгого порядка с отношением равенства совпадает с отношением нестрого порядка, а их пересечение пусто.
, то есть объединение отношения строгого порядка с отношением равенства совпадает с отношением нестрого порядка, а их пересечение пусто.
Кроме перечисленных важное значение имеют еще операции обращения и умножения отношений, определяемые следующим образом. Если  , то обратным отношением называется отношение
, то обратным отношением называется отношение 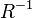 , определенное на паре
, определенное на паре  ,
, 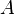 и состоящее из тех пар
и состоящее из тех пар 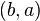 , для которых
, для которых 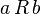 . Например,
. Например,  .
.
Пусть  ,
, 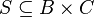 . Композицией (или произведением) отношений
. Композицией (или произведением) отношений  и
и  называется отношение
называется отношение 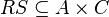 такое, что:
такое, что:
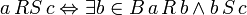 .
.
Например, для отношения строгого порядка на множестве натуральных числе его умножение на себя определено следующим образом: 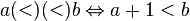 .
.
Бинарные отношения и
и  называются перестановочными, если
называются перестановочными, если  . Для любого бинарного отношения
. Для любого бинарного отношения  , определенного на
, определенного на 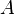 , имеет место
, имеет место  , где символом
, где символом  обозначено равенство, определенное на
обозначено равенство, определенное на 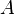 . Однако равенство
. Однако равенство 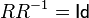 не всегда справедливо.
не всегда справедливо.
Имеют место следующие тождества:
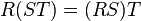 ,
, ,
, ,
, ,
,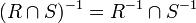 ,
,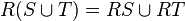 ,
,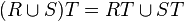 .
.Аналоги последних двух тождеств для пересечения отношений не имеют места.
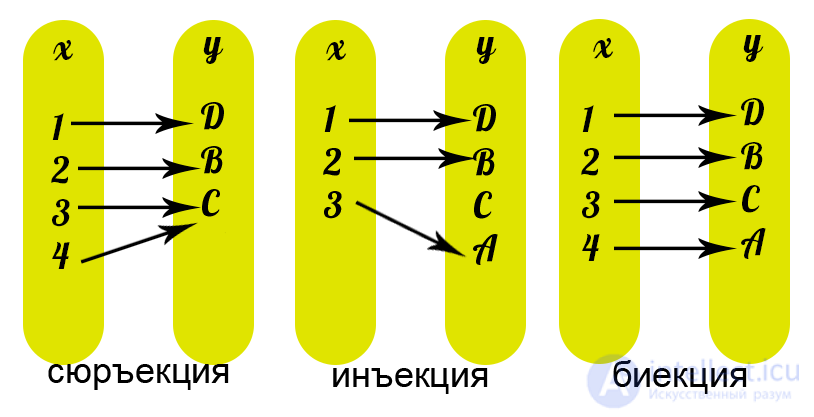
- Отображение f:x->y называется СЮРЪЕКЦИЕЙ, если Ay∈Y ∃ x∈X:y=f(x). Тогда y - образ, x - прообраз y.
- Отображение f:x->y называется ИНЪЕКЦИЕЙ, если x1 ≠ x2 => f(x1)≠f(x2), те разные элементы множества X переводятся в разные элементы множества Y.
или f(x1)≠f(x2) => x1=x2
- Отображение f:x->y называется БИЕКЦИЕЙ, если оно одновременно сюръективно и инъективно. При биективном отражении каждому элементу одного множества соответсвует ровно один элемент другого множества, при этом определено обратное отображение, которое обладает теми же свойствами.
Бинарное отношение 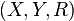 называется
называется
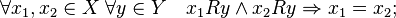
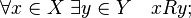
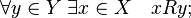
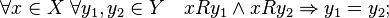
Бинарное отношение на множестве называется отношением частичного порядка , если оно удовлетворяет свойствам
Определение. Бинарное отношение f называется функцией, если из Îf и Îf следует, что y=z.
Поскольку функции являются бинарными отношениями, то две функции f и g равны, если они состоят из одних и тех же элементов. Область определения функции обозначается Df, а область значений – Rf. Определяются они так же, как и для бинарных отношений.
Если f – функция, то вместо Îf пишут y=f(x) и говорят, что y – значение, соответствующее аргументу х, или y – образ элемента х при отображении f. При этом хназывается прообразом элемента y.
Определение. Назовем f n-местной функцией из Х в Y если f:Xn®Y. Тогда пишем y=f(x1, x2, …, xn) и говорим, что y – значение функции при значении аргументов x1, x2, …, xn.
Пусть f:X®Y.
Определение. Функция f называется инъективной, если для любых х1, х2, y из y=f(x1) и y=f(x2) следует, что x1=x2, то есть каждому значению функции соответствует единственное значение аргумента.
Определение. Функция f называется сюръективной, если для любого элемента yÎY существует элемент хÎХ такой, что y=f(x).
Определение. Функция f называется биективной, если f одновременно сюръективна и инъективна.
Рисунок 9 иллюстрирует понятия отношения, функции, инъекции, сюръекции и биекции.

Пример 9.
Рассмотрим три функции, заданные на множестве действительных чисел и принимающих значение в этом же множестве:
Ну вот возьмем два множества: множество учеников и множество стульев в классе. И будем устанавливать соответсвие между этими двумя множествами, т. е. просто рассаживать учеников на стулья.
1. Если каждый ученик сел на отдельный стул (некоторые стулья могут остаться свободными) , то это инъекция. Понятно, что при таком отображение количество стульев не может быть меньше количества учеников (ученики не могут садится по два на один стул) .
2. Если все стулья оказались заняты (на некоторых могут сидеть и по два или больше учеников) , то это сюръекция. В этом случает уже количество учеников не может быть меньше стульев.
3. Если каждый ученик сидит на отдельном стуле, и нет ни свободных стульев, ни учеников, которым стульев не хватило - это биекция. Т. е. биекция это одновременно и инъекция (каждый ученик сидит на отдельном стуле) и сюръекция (все стулья заняты) . Для возможности такого отображения (биекции) количество учеников должно быть в точности равно количеству стульев.
Естественно вместо учеников и стульями может быть что угодно, например числовые множества.
Все эти соответсвия могут устанавляваться и между бесконечными множествами. И кроме того, между конечным и бесконечным - инъекция, или бесконечным и конечным - сюръекция.
Надеюсь, эта статья про бинарное отношение, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое бинарное отношение, биекция, сюръекция, инъекция и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.