Структура упорядоченных множеств кратко

Привет, сегодня поговорим про структура упорядоченных множеств, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое структура упорядоченных множеств , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

Пусть М – множество, упорядоченные некоторым отношением порядка А, а Q – некоторое его подмножество QÌ M. Тогда Мажо­Рантой (верхней границей) Подмножества Q Ì M называют такой элемент M Î M, что для всехQ Î Q справедливо соотношение Q А M.

Например: Пусть М – множество натуральных чисел от 1 до 10, т. е. М = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, а Q – подмножество Q = {5, 6, 7}. Если А – это отношение порядка £, то мажорантой подмножества Q Ì M является такой элемент M Î M, для которого выполняется условие 5 £ M; 6 £ M; 7 £ M. Таким элементом является, например, M = 8 (а также M = 9 и M = 10).

Минорантой (нижней границей) Подмножества Q Ì M назы­вается такой элемент M Î M, когда для всех Q Î Qвыполняется соотношение M А Q.

Например: Для условий предыдущего примера минорантой является такой элемент M Î M, для которого выполняются соотношения M £ 5; M £ 6; M £ 7. Об этом говорит сайт https://intellect.icu . Таким элементом является, например, M = 4 (а также M = 3; M= 2; M = 1).

Множество Q Ì M может иметь много мажорант и минорант.

Если множество мажорант имеет минимум, то этот элемент единственный. Его называют Верхней гранью или супремумом Мно­жества Q и обозначают Sup Q.

Если множество минорант имеет максимум, то этот элемент единственный. Его называют Нижней гранью или инфинумом Мно­жества Q и обозначают Inf Q.

Если мажоранта (или миноранта) принадлежит множеству Q, то она называется максимумом (или минимумом) множества Q – max Q (min Q). Максимум, как и минимум, единственный (если он сущест­вует). Поэтому, когда говорят о максимуме или минимуме, то это элемент единственный и вполне определенный.

Для нашего примера Q = 7 – это max Q, а Q = 5 – это min Q.

Базовые понятия:

• множество,
• подмножество,
• бинарное отношение,
• рефлексивность,
• симметричность,
• транзитивность

Ключевые слова:

• бинарное отношение порядка,
• рефлексивность,
• антисимметричность,
• транзитивность,
• старший элемент,
• наибольший (наименьший) элемент,
• мажоранта (миноранта),
• верхняя (нижняя) грань,
• супремум (инфимум)

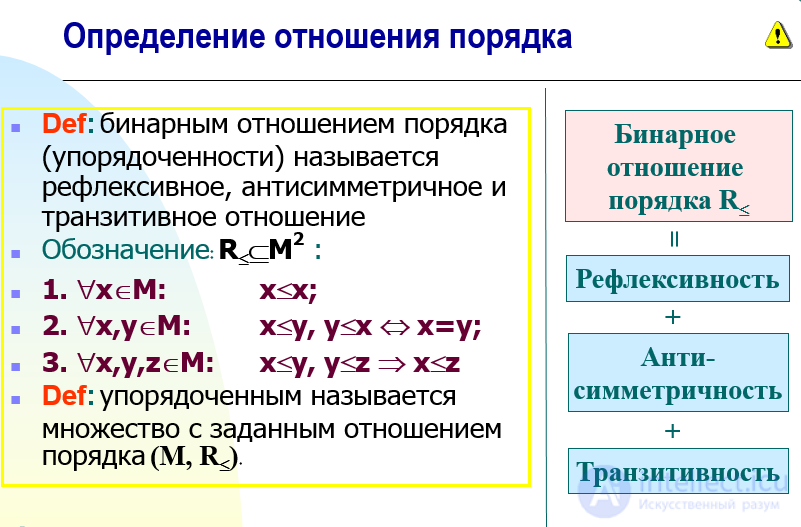
Определение отношения порядка

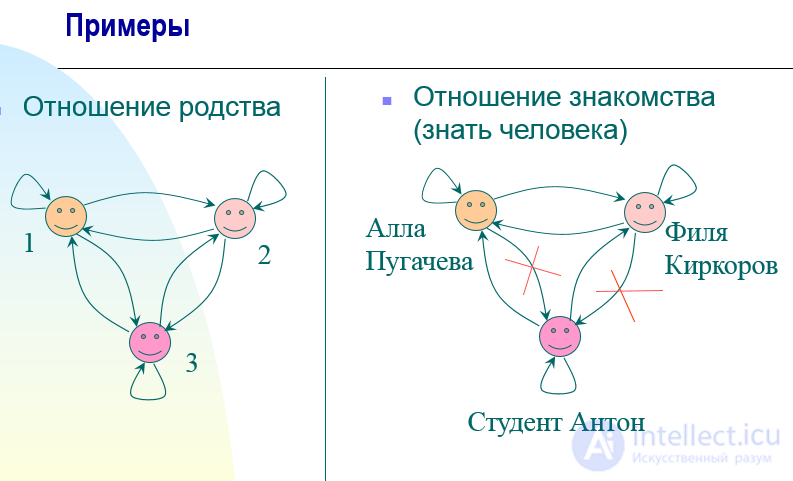
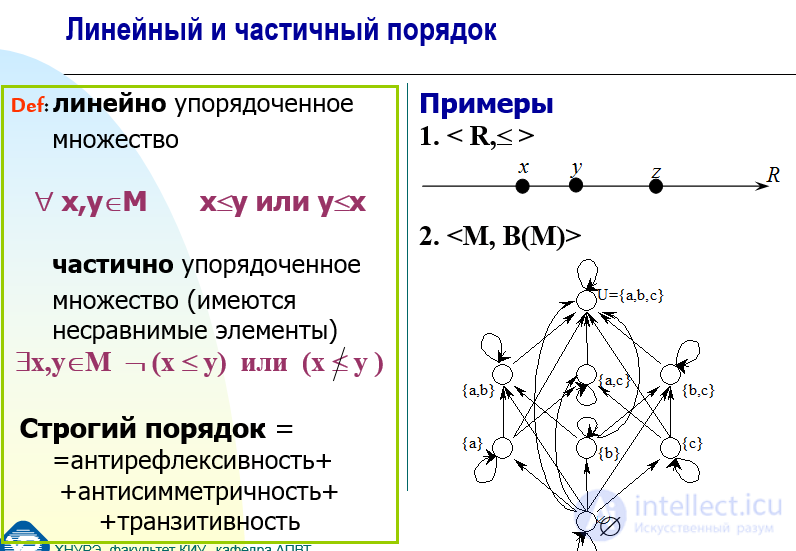
Линейный и частичный порядок

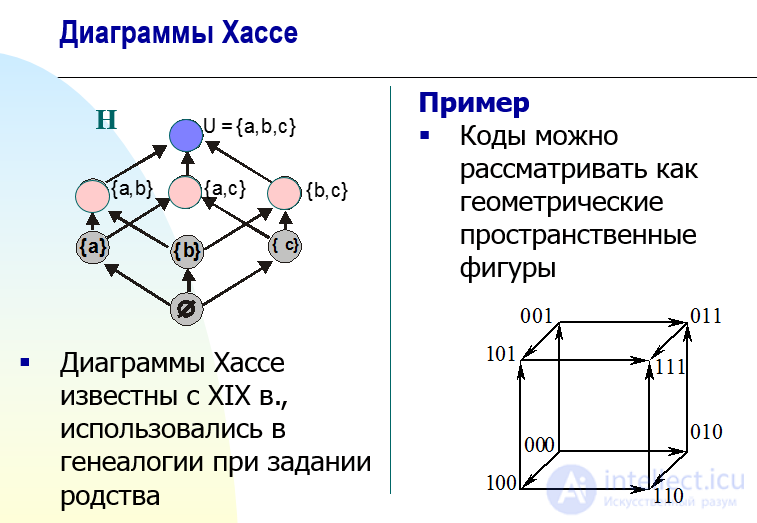
Диаграмы Хассе

Отношение покрываемости в упорядоченном множестве

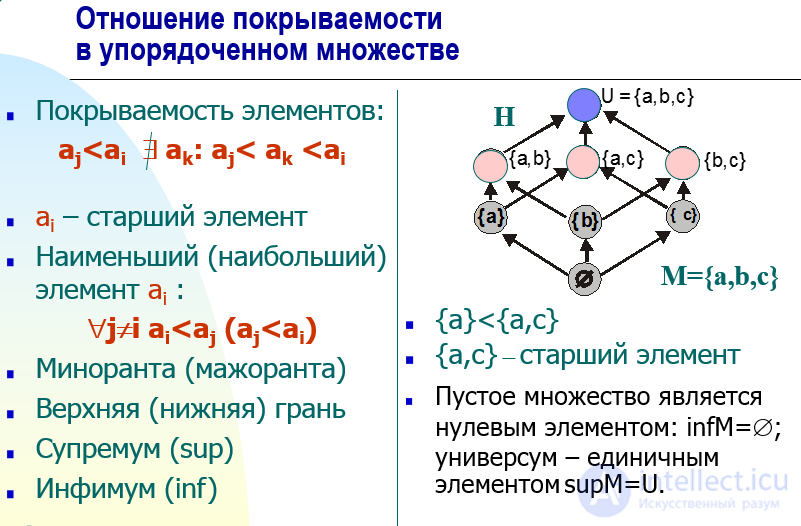
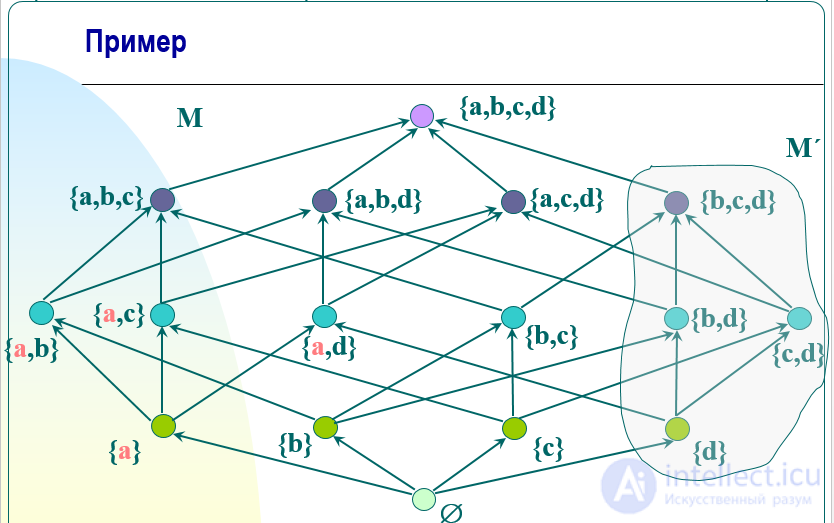
Единственность наибольшего (наименьшего) элемента

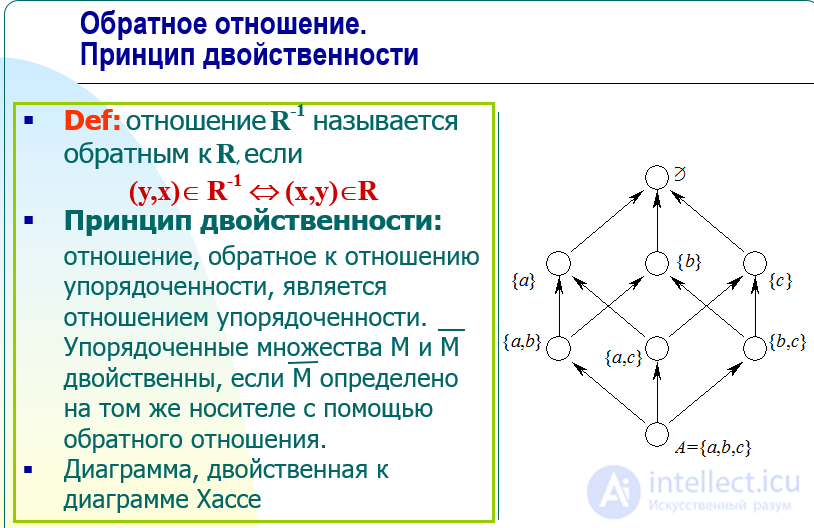
Обратное отношение.
Принцип двойственности

Надеюсь, эта статья про структура упорядоченных множеств, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое структура упорядоченных множеств и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.

Из статьи мы узнали кратко, но содержательно про структура упорядоченных множеств