Проблема четырёх красок

Привет, сегодня поговорим про проблема четырёх красок, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое проблема четырёх красок , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

 

Проблема четырех красок

 

Административная карта России, раскрашенная в четыре цвета

В математике теорема о четырех красках утверждает, что всякую расположенную на сфере карту можно раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета. При этом считается, что каждая область является односвязной, а под общим участком границы понимается часть линии, то есть стыки нескольких областей в одной точке общей границей для них не считаются. Эта теорема была сформулирована Фрэнсисом Гутри (англ.) в1852 году, однако доказать ее долгое время не удавалось. В течение этого времени было предпринято множество попыток как доказательства, так и опровержения, и эта задача носила название проблемы четырех красок.

Задача раскраски карты на плоскости эквивалентна задаче на сфере.

Для простых карт достаточно и трех цветов, а четвертый цвет начинает требоваться, например, тогда, когда имеется одна область, окруженная нечетным числом других, которые соприкасаются друг с другом, образуя цикл. Теорема о пяти красках, утверждающая, что достаточно пяти цветов, имела короткое несложное доказательство и была доказана в конце XIX века, но доказательство теоремы для случая четырех цветов столкнулось со значительными трудностями.

Теорема о четырех красках была доказана в 1976 году Кеннетом Аппелем (англ.) и Вольфгангом Хакеном (англ.) из Иллинойского университета. Это была первая крупная математическая теорема, доказанная с помощью компьютера. Первым шагом доказательства была демонстрация того, что существует определенный набор из 1936 карт, ни одна из которых не может содержать карту меньшего размера, которая опровергала бы теорему. Аппель и Хакен использовали специальную компьютерную программу, чтобы доказать это свойство для каждой из 1936 карт. Доказательство этого факта заняло сотни страниц. После этого Аппель и Хакен пришли к выводу, что не существует наименьшего контрпримера к теореме, потому что иначе он должен бы содержать, хотя не содержит, какую-нибудь из этих 1936 карт. Это противоречие говорит о том, что вообще не существует контрпримера. Изначально доказательство не было принято всеми математиками, поскольку его невозможно было проверить вручную. Об этом говорит сайт https://intellect.icu . В дальнейшем оно получило более широкое признание, хотя у некоторых долгое время оставались сомнения.

Чтобы развеять оставшиеся сомнения, в 1997 году Робертсон, Сандерс, Сеймур и Томас опубликовали более простое доказательство, использующее аналогичные идеи, но по-прежнему проделанное с помощью компьютера. Кроме того, в 2005 году доказательство было проделано Джорджсом Гонтиром с использованием специализированного программного обеспечения (Coqv7.3.1)^[1].

Эквивалентные формулировки[править ]

В теории графов  утверждение теоремы четырех красок имеет следующие формулировки:

• Хроматическое число  плоского графа не превосходит 4.
• Ребра произвольной триангуляции сферы можно раскрасить в три краски так, что все стороны каждого треугольника были раскрашены в разные цвета.

История доказательства[править ]

Наиболее известные попытки доказательства:

• Альфред Кэмпе предложил доказательство в 1879 году^[2], его опровергли в 1880 году, на основе его идей удалось доказать, что любую карту можно раскрасить в 5 цветов.
• Питер Тэт предложил другое доказательство в 1880 году^[3], его опровергли в 1891 году.
• В своей книге^[4] В. А. Горбатов утверждает, что предложил классическое доказательство еще в 1964 году (объемом около 30 стр.). Однако опровержений, как и подтверждений, это доказательство пока не получило.

Вариации и обобщения[править ]

Аналогичные задачи для других поверхностей (тор,  бутылка Клейна  и т. д.) оказались значительно проще. Для всех замкнутых поверхностей, кроме сферы (и ей эквивалентных плоскости и цилиндра) и бутылки Клейна, необходимое число красок может быть вычислено через эйлерову характеристику 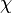 по формуле, предложенной в 1890 году Перси Джоном Хивудом (Percy John Heawood)^[5] и окончательно доказанной на протяжении 1952—1968 годов группой математиков с наибольшим вкладом Герхарда Рингеля и Теда Янгса (Gerhard Ringel and J. T. W. Youngs)^[6][7]

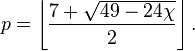
Для бутылки Клейна число равно 6 (а не 7, как по формуле) — это показал П. Франклин в 1934 году,^[8] а для сферы — 4.

Для односторонних поверхностей^[7]

.

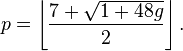В старших размерностях разумного обобщения задачи не существует, так как легко придумать уже трехмерную карту с произвольным числом областей, которые все друг друга касаются.

Игра «четыре краски»[править ]

Стивен Барр предложил логическую игру на бумаге для двух игроков, названную «Четыре краски». По словам Мартина Гарднера — «Я не знаю лучшего способа понять трудности, которые встречаются на пути решения проблемы четырех красок, чем просто поиграть в эту любопытную игру»^[9].

Для этой игры нужны четыре цветных карандаша. Первый игрок начинает игру, рисуя произвольную пустую область. Второй игрок закрашивает ее любым из четырех цветов и в свою очередь рисует свою пустую область. Первый игрок закрашивает область второго игрока и добавляет новую область, и так далее — каждый игрок раскрашивает область соперника и добавляет свою. При этом области, имеющие общую границу, должны быть раскрашены в разные цвета. Проигрывает тот, кто на своем ходу вынужден будет взять пятую краску.

Стоит отметить, что в этой игре проигрыш одного из игроков вовсе не является доказательством неверности теоремы (четырех красок оказалось недостаточно!). А лишь иллюстрацией того, что условия игры и теоремы весьма разнятся. Чтобы проверить верность теоремы для полученной в игре карты, нужно проверить связность нарисованных областей и, удалив с нее цвета, выяснить, можно ли обойтись лишь четырьмя цветами для закрашивания получившейся карты ( теорема утверждает, что можно).

Существуют также следующие вариации игры:

1. Карта заранее разбивается случайным образом на области различной величины, и каждый ход игры меняется игрок который закрашивает область, а также меняется цвет (в строгой последовательности). Таким образом каждый игрок закрашивает карту только двумя цветами, а в случае если не может закрасить так, чтобы области, имеющие общую границу были раскрашены в разные цвета. пропускает ход. Игра прекращается когда ни один из игроков больше не сможет сделать ни одного хода. Выигрывает тот, у кого общая площадь закрашенных им областей больше.
2. Квадрат разбит на несколько квадратов (в основном 4x4), и его стороны окрашены в один из четырех цветов (каждый в разный цвет ). Первым ходом закрашивается квадрат прилегающий к стороне, каждый последующий ход можно закрашивать тот квадрат, который прилегает к одному из закрашенных квадратов. Нельзя закрашивать квадрат теми цветами, которыми закрашен один из прилегающих к нему квадратов (в том числе и по диагонали) или прилегающая к квадрату сторона. Выигрывает игрок, делающий последний ход.

В культуре[править ]

• «Остров пяти красок» — фантастический рассказ Мартина Гарднера^[10].

Вау!! 😲 Ты еще не читал? Это зря![править ]

• Доказательные вычисления

Примечания[править ]

Надеюсь, эта статья про проблема четырёх красок, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое проблема четырёх красок и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.