Отношение эквивалентности в теории множеств кратко

Привет, сегодня поговорим про отношение эквивалентности, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое отношение эквивалентности , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

отношение эквивалентности — бинарное отношение между элементами данного множества, свойства которого сходны со свойствами отношения равенства.

Определение

Отношение эквивалентности () на множестве — это бинарное отношение, для которого при любых из выполнены следующие условия:

1. рефлексивность: ;
2. симметричность: если , то ;
3. транзитивность: если и , то .

Запись вида «» читается как « эквивалентно ».

Отношение эквивалентности представляет собой строгое матема­тическое определение таких обыденных понятий как «одинаковость» или «неразличимость».

Обозначается X~Y. Отношение эквивалентности А в множестве М означает, что упорядоченная пара (X, Y) принадлежит множеству А Ì М´М.

Отношение эквивалентности обладает свойствами:

· Рефлексивности: X~Y;

· Симметричности: если X~Y, то Y~X;

· Транзитивности: если X~Y и Y~Z, то X~Z.

Важнейшее значение эквивалентности состоит в том, что это отношение определяет признак, который допускает разбиение множества М на непересекающиеся подмножества, называемые Клас­Сами эквивалентности. И наоборот: всякое разбиение множества М на непересекающиеся подмножества определяет между элементами этого множества некоторое отношение эквивалентности.

Например: Отношение «проживать в одном доме», заданное в множестве жителей города, является эквивалентностью и разбивает это множество на непересекающиеся подмножества людей, являющихся соседями по дому.

Все элементы, принадлежащие некоторому классу МI разбиения {М1, М2,..., МN} множества М на классы эквивалентности, связаны отношением эквивалентности. Любой из этих элементов определяет данный класс и может служить его Представителем или Эталоном.

Произвольное отношение эквивалентности определяет на некотором множестве обобщенную форму равенства. Классы эквивалентности состоят из всех тех элементов, которые неразличимы с точки зрения данного отношения эквивалентности. При этом каждый класс определяется его представителем (эталоном) и отождествляется с некоторым общим свойством или совокупностью свойств входящих в него элементов.

Предельным случаем отношения эквивалентности является Тождественное равенство. Очевидно, что единственный элемент, тождественно равный какому-либо данному элементу, есть этот самый элемент. Следовательно, в данном случае имеем самое полное разбиение, при котором классы эквивалентности содержат только по одному элементу исходного множества.

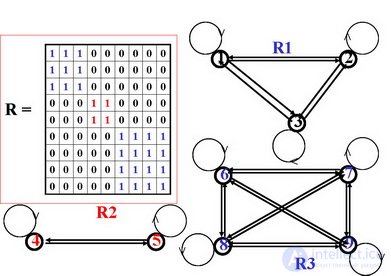
Рассмотрим матрицу отношения эквивалентности.

Элементы, принадлежащие некоторому классу эквивалентности, попарно эквивалентны между собой, а их сечения совпадают. Сле­довательно, столбцы матрицы отношения эквивалентности для элемен­тов одного класса одинаковы и содержат «1» во всех строках, которые соответствуют этим элементам. Так как классы эквивалентности не пересекаются, то в столбцах различных классов не будет единиц в одинаковых строках. Если расположить элементы множества так, чтобы в каждом классе эквивалентности принадлежащие ему элементы стояли рядом, то единичные элементы матрицы образуют непересекаю­щиеся квадраты, диагонали которых располагаются на главной диагонали матрицы.

Например: Пусть множество М разбито на классы эквивалент­ности следующим образом:

М1 = {Х1, х2, х3}; М2 = {Х4}; М3 = {Х5, х6, х7, х8}.

Признаки, по которым элементы множества разбиваются на классы, могут быть самыми разнообразными, но все же такой признак не вполне произволен.

Xi Xj	X1	X2	X3	X4	X5	X6	X7	X8
X1	1	1	1
X2	1	1	1
X3	1	1	1
X4				1
X5					1	1	1	1
X6					1	1	1	1
X7					1	1	1	1
X8					1	1	1	1

Предположим, Например, что мы хотим разбить точки плоскости на классы, относя две точки к одному классу в том, и только в том случае, когда расстояние между ними меньше 1. Об этом говорит сайт https://intellect.icu . Пусть расстояние от точки А до точки Bменьше 1, и расстояние от B До С тоже меньше 1. Тогда, относя А в один класс с B, а B в один класс с С , мы должны отнести С в один класс с А. Но расстояние от А до С может быть и больше 1. Следовательно, такой признак не позволяет разбить мно­жество на классы эквивалентности. Это объясняется тем, что для него не выполняется свойство транзитивности: если А ~ B, а B ~ С, то А ~ С. Таким образом, можно определить отношение эквивалентности как бинарное отношение, для которого выполняются свойства рефлексив­ности, симметричности и транзитивности.

Выполнение этих условий является необходимым и достаточным для того, чтобы данный признак позволял разбить множество на классы эквивалентности.

Пример: на множестве из 6-ти ниже приведенных графов



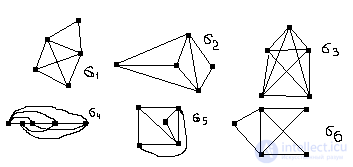
построим граф, соответствующий отношению эквивалентности.

Решение:

т.к. отношение эквивалентности на множестве объектов есть совокупность трех свойств – рефлективности, симметричности и транзитивности, то имеем:



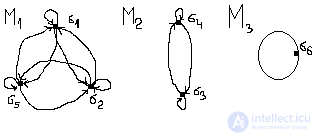
Здесь: М₁М={σ₁,σ₂,σ₃,σ₄,σ₅,σ₆}, М_i – множество попарно изолированных графов, т.е. М₁={ σ₁,σ₂,σ₅}. Аналогично М₂М и М₂={ σ₃,σ₄}, М₃М и М₃={ σ₆}. Итак, отношением эквивалентности множество М из 6-ти графов разбивается на три непересекающихся подмножества изоморфных графов М₁М₂=Ø, М₁М₃=Ø, М₂М₃=Ø, M₁M₂M₃=M.

Иллюстративные примеры отношений эквивалентности

Связанные определения

Классом эквивалентности элемента называется подмножество элементов, эквивалентных ; то есть,

.

Из вышеприведенного определения немедленно следует, что если , то .

Фактормножество — множество всех классов эквивалентности заданного множества по заданному отношению , обозначается .

Для класса эквивалентности элемента используются следующие обозначения: , , .

Множество классов эквивалентности по отношению является разбиением множества.

Примеры

• Равенство («»), тривиальное отношение эквивалентности на любом множестве, в частности, вещественных чисел.
• Сравнение по модулю: а ≡ b (mod n).
• В евклидовой геометрии
  • Отношение конгруэнтности («»).
  • Отношение подобия («»).
  • Отношение параллельности прямых («») (но только если дополнительно к принятому определению считать каждую прямую параллельной самой себе).
• Эквивалентность функций в математическом анализе:

  Говорят, что функция эквивалентна функции при , если она допускает представление вида , где при . В этом случае пишут , напоминая при необходимости, что речь идет о сравнении функций при . Если при , эквивалентность функций и при , очевидно, равносильна соотношению .

• Эквивалентность норм на векторном пространстве.
• Отношение равномощности множеств.
• Изоморфизм групп, колец, векторных пространств
• Эквивалентность категорий.
• Изоморфизм в некоторой категории задает отношение эквивалентности на этой категории.
• Эквивалентность гладких атласов гладкого многообразия.

Классы эквивалентности

Множество всех классов эквивалентности, отвечающее отношению эквивалентности , обозначается символом и называется фактормножеством относительно . При этом сюръективное отображение

называется естественным отображением (или канонической проекцией) на фактормножество .

Пусть и — множества, — отображение, тогда бинарное отношение , определенное правилом

,

является отношением эквивалентности на . При этом отображение индуцирует отображение , определяемое правилом

или, что то же самое,

.

При этом получается факторизация отображения на сюръективное отображение и инъективное отображение .

Вау!! 😲 Ты еще не читал? Это зря!

• Отношение толерантности — ослабленная форма эквивалентности.
• Отношение порядка отношение порядка ,
• бинарное отношение , биекция , сюръекция , инъекция ,
• отношение строгого порядка , отношение не строгого порядка ,
• Эквиваленция — логическая операция .
• Знак равенства.

Надеюсь, эта статья про отношение эквивалентности, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое отношение эквивалентности и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.

Из статьи мы узнали кратко, но содержательно про отношение эквивалентности