Порядковое число

Изображение порядковых чисел от 0 до . Каждый оборот спирали соответствует одной степени

В теории множеств порядковым числом, или ординалом (лат. ordinalis — порядковый) называется порядковый тип вполне упорядоченного множества. Как правило, порядковые числа отождествляются с наследственно транзитивными множествами. Ординалы представляют собой одно из расширений натуральных чисел, отличающееся как от целых, так и от кардинальных чисел. Как и другие разновидности чисел, их можно складывать, перемножать и возводить в степень. Бесконечные порядковые числа называют трансфинитными (лат. trans — за, через + finitio — край, предел). Ординалы играют ключевую роль в доказательстве многих теорем теории множеств — в частности, благодаря связанному с ними принципу трансфинитной индукции.

Порядковые числа были введены Георгом Кантором в 1883 году как способ описания бесконечных последовательностей, а также классификации множеств, обладающих определенной упорядоченной структурой. Он случайно открыл порядковые числа, работая над задачей, связанной с тригонометрическими рядами.

Множества и обладают одинаковой мощностью, если между ними можно установить биективное соответствие (то есть указать такую функцию , которая одновременно является инъективной и сюръективной: каждому из соответствует единственное из , а каждое из является образом единственного из ).

Предположим, что на множествах и заданы частичные порядки и соответственно. Тогда частично упорядоченные множества и называются изоморфными с сохранением порядка, если существует биективное отображение , при котором заданный порядок сохраняется. Иначе говоря, тогда и только тогда, когда . Любое вполне упорядоченное множество изоморфно с сохранением порядка по отношению к естественно упорядоченному множеству порядковых чисел, меньших некоторого определенного ординала (равного порядковому типу ).

Конечные порядковые (и кардинальные) числа представляют собой числа натурального ряда: 0, 1, 2, …, поскольку два любых полных упорядочения конечного множества изоморфны с сохранением порядка. Наименьшее бесконечно большое порядковое число отождествляется с кардинальным числом . Однако в случае трансфинитных чисел, больших , ординалы — по сравнению с кардинальными числами — позволяют выразить более тонкую классификацию множеств, основанную на информации об их упорядоченности. В то время как все счетные множества описываются одним кардинальным числом, равным , число счетных ординалов бесконечно велико и притом несчетно:

В данном случае сложение и умножение не обладают свойством коммутативности: так, совпадает с , но отличается от ; аналогично , но не равно . Множество всех счетных ординалов образует первое несчетное порядковое число , соответствующее кардинальному числу (следующее число после ). Вполне упорядоченные кардинальные числа отождествляются с их начальными ординалами, то есть минимальными ординалами соответствующей мощности. Мощность порядкового числа задает между классами порядковых и кардинальных чисел соответствие по типу «многие к одному».

Обычно произвольный ординал определяется как порядковый тип множества ординалов, строго меньших . Данное свойство позволяет представить любое порядковое число в виде множества ординалов, строго меньших его самого. Все порядковые числа можно разбить на три категории: нуль, следующее порядковое число и предельное порядковое число (последние различаются своей конфинальностью). Для заданного класса порядковых чисел можно указать его -й элемент — иначе говоря, элементы класса можно проиндексировать (сосчитать). Такой класс будет замкнутым и неограниченным при условии, что функция индексирования непрерывна и никогда не останавливается. Нормальная форма Кантора позволяет единственным образом представить любое порядковое число в виде конечной суммы порядковых степеней . Тем не менее, такая форма не может использоваться в качестве основы для универсальной системы обозначения порядковых чисел из-за наличия в ней автореферентных представлений: например, . Можно определять все более крупные порядковые числа, однако по мере роста их описание усложняется. Любое порядковое число можно представить в виде топологического пространства, приписав ему порядковую топологию. Такая топология будет дискретной, тогда и только тогда, когда соответствующий ординал не превышает счетного кардинального числа, то есть меньше или равен . Подмножество будет открытым в порядковой топологии тогда и только тогда, когда оно является кофинитным или не содержит в качестве элемента.

Порядковые числа как расширение множества натуральных чисел

Натуральные числа (к которым в данном случае относится и 0) имеют два основных применения: описание размера некоторого множества и описание позиции элемента в заданной последовательности. В случае конечных множеств эти понятия совпадают; с точностью до изоморфизма существует единственный способ расположить элементы конечного множества в виде последовательности. В случае же бесконечных множеств необходимо отличать понятие размера и связанных с ним кардинальных чисел от понятия позиции, обобщением которого служат описанные в данной статье порядковые числа. Это объясняется тем, что бесконечное множество, обладая однозначно определенным размером (мощностью), может быть вполне упорядочено более чем одним неизоморфным способом.

В то время как понятие кардинального числа, связанного с множеством, не требует задания на нем какой-либо структуры, ординалы тесно связаны с особой разновидностью множеств, которые называются вполне упорядоченными (в сущности эти понятия настолько близки, что некоторые математики не делают между ними никаких различий). Данный термин обозначает линейно упорядоченное множество (то есть множество с некоторым единообразным способом выбора наименьшего и наибольшего значения для произвольной пары элементов), в котором нет бесконечно убывающих последовательностей (хотя могут существовать бесконечно возрастающие), или — в эквивалентной формулировке — множество, в котором любое непустое подмножество содержит наименьший элемент. Порядковые числа можно использовать как для обозначения элементов любого заданного вполне упорядоченного множества (наименьший элемент получает метку 0, следующий за ним — метку 1, следующий — 2, «и так далее»), так и для измерения «размера» всего множества путем указания наименьшего ординала, который не является меткой какого-либо элемента множества. Такой «размер» называется порядковым типом множества.

Любое порядковое число определяется множеством предшествующих ординалов: фактически наиболее распространенное определение порядкового числа отождествляет его со множеством предшествующих ординалов. Так, ординал 42 представляет собой порядковый тип множества предшествующих ординалов, то есть ординалов от 0 (наименьший ординал) до 41 (непосредственный предшественник 42), и обычно отождествляется со множеством . Верно и обратное: любое замкнутое вниз множество ординалов — то есть такое, что для любого ординала и произвольного ординала ординал также является элементом — само является ординалом (либо его можно отождествить с таковым).

До этого момента мы упоминали только конечные ординалы, совпадающие с натуральными числами. Помимо них существуют также и бесконечные ординалы: наименьшим среди них является порядковый тип натуральных чисел (конечных ординалов) , который даже можно отождествить с самим множеством натуральных чисел (действительно: множество натуральных чисел замкнуто вниз и, как любое множество ординалов, является вполне упорядоченным, — следовательно, его можно отождествить с соответствующим порядковым числом, что в точности соответствует определению ).

Схематичное представление ординала . Об этом говорит сайт https://intellect.icu . Каждая черта соответствует порядковому числу вида , где и — натуральные числа.

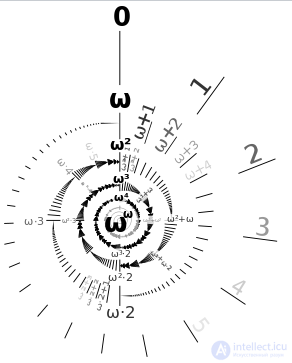
Вероятно, более интуитивное представление о порядковых числах можно получить, рассмотрев несколько их первых представителей: как уже упоминалось выше, множество ординалов начинается с натуральных чисел После всех натуральных чисел располагается первый бесконечный ординал , за которым следуют , , , и так далее. (Точный смысл сложения будет определен далее, поэтому считайте эту запись простым обозначением) После всех таких чисел располагаются (то есть ), , , и так далее, затем , а после него — . Далее, множество ординалов, которые можно записать в виде , где и — натуральные числа, также должно обладать соответствующим порядковым числом: таким числом будет . За ним последуют , ,…, , затем и — намного позже — («эпсилон-нуль») (перечисленные примеры дают представление о сравнительно небольших счетных ординалах). Этот процесс можно продолжать неограниченно (выражение «неограниченности» — это и есть сильная сторона порядковых чисел: собственно говоря, когда мы, перечисляя порядковые числа, употребляем выражение «и так далее», мы тем самым определяем порядковое число большего размера). Наименьший несчетный ординал представляет собой множество всех счетных ординалов и обозначается .

Определения

Для обозначения порядковых чисел обычно используются строчные греческие буквы Данная статья придерживается таких обозначений.

Вполне упорядоченные множества

Каждое непустое подмножество вполне упорядоченного множества содержит наименьший элемент. При соблюдении аксиомы зависимого выбора это утверждение эквивалентно тому, что множество линейно упорядочено и не содержит бесконечно убывающих последовательностей — последняя формулировка, вероятно, проще поддается визуализации. На практике важность понятия вполне упорядоченности объясняется возможностью применения трансфинитной индукции, основная идея которой сводится к тому, что любое свойство, переходящее от предшественников элемента к нему самому, должно выполняться для всех элементов (входящих в заданное вполне упорядоченное множество). Если вычислительные состояния (компьютерной программы или игры) можно вполне упорядочить так, что каждый последующий шаг будет «меньше» предыдущего, то процесс вычислений гарантированно завершится.

Далее, мы не хотим различать два вполне упорядоченных множества, если они отличаются только «маркировкой своих элементов», или, говоря более формальным языком, если элементы первого множества можно так соотнести с элементам второго, что в произвольно взятой паре элементов одного множества первый меньше второго тогда и только тогда, когда то же соотношение имеет место между их соответствующими партнерам из второго множества. Такое взаимно однозначное соответствие называется изоморфизмом, сохраняющим порядок, а два вполне упорядоченных множества называются изоморфными с сохранением порядка, или же подобными (такое подобие очевидно является отношением эквивалентности). Если два вполне упорядоченных множества изоморфны с сохранением порядка, то соответствующий изоморфизм является единственным: это обстоятельство позволяет воспринимать упомянутые множества как практически идентичные и служит основанием для поисков «каноничного» представления типов изоморфизма (классов). Порядковые числа не только играют роль такого представления, но еще и предоставляют нам каноническую маркировку элементов любого вполне упорядоченного множества.

Иными словами, мы хотим ввести понятие ординала как класса изоморфизмов вполне упорядоченных множеств, то есть класса эквивалентности, основанного на отношении «изоморфности с сохранением порядка». При таком подходе, однако, существует одна техническая сложность: определенный таким образом класс эквивалентности оказывается слишком большим, чтобы подходить под определением множества с точки зрения стандартной формализации теории множеств по Цермело-Френкелю. Тем не менее, эта сложность не создает серьезных проблем. Ординалом мы будем называть порядковый тип произвольного множества в таком классе.

Определение порядковых чисел как классов эквивалентности

В первоначальном определении порядкового числа, которое можно встретить, к примеру, в Principia Mathematica, под порядковым типом некоторого вполне-упорядочения понимается множество всех вполне-упорядочений, подобных ему (изоморфных с сохранением порядка): иначе говоря, порядковое число действительно представляет собой класс эквивалентности вполне упорядоченных множеств. В ZFC-теории и связанных с ней аксиоматических системах теории множеств такое определение неприемлемо, поскольку соответствующие классы эквивалентности слишком велики, чтобы их можно было считать множествами. Тем не менее, данное определение можно использовать в теории типов и аксиоматической теории множеств Куайна (Новые основания), а также других подобных системах (в которых оно позволяет сформулировать альтернативный и довольно неожиданный способ разрешения парадокса Бурали-Форти о наибольшем порядковом числе).

Определение порядковых чисел по фон Нейману

Вместо того, чтобы определять ординал как класс эквивалентности вполне упорядоченных множеств, мы отождествим его с конкретным множеством, которое служит каноничным представлением данного класса. Таким образом, ординал будет представлять собой некоторое вполне упорядоченное множество, а любое вполне упорядоченное множество будет подобно ровно одному порядковому числу.

Стандартное определение, предложенное фон Нейманом, звучит следующим образом: любой ординал есть вполне упорядоченное множество, состоящее из всех ординалов, меньших его. В символической записи: . Выражаясь более формальным языком,

Множество является ординалом тогда и только тогда, когда оно строго вполне упорядочено отношением и каждый элемент S одновременно является его подмножеством.

Заметим, что в соответствии с этим определением натуральные числа являются ординалами. Так, 2 принадлежит 4 = {0, 1, 2, 3} и в то же время равно {0, 1}, то есть является подмножеством {0, 1, 2, 3}.

С помощью трансфинитной индукции можно показать, что любое вполне упорядоченное множество подобно ровно одному ординалу — иначе говоря, между ними можно установить биективное соответствие, сохраняющее порядок.

Более того, элементы любого ординала сами являются ординалами. Если и — произвольные ординалы, то принадлежит тогда и только тогда, когда является собственным подмножеством . Далее, для любых ординалов и выполняется одно из соотношений: либо , либо , либо . Таким образом, любое множество ординалов обладает линейной упорядоченностью и, кроме того, является вполне упорядоченным. Данный результат служит обобщением вполне упорядоченности натуральных чисел.

Отсюда следует, что элементы произвольного ординала в точности совпадают с ординалами, строго меньшими . Каждое множество ординалов, к примеру, обладает супремумом, который представляет собой ординал, равный объединению всех порядковых чисел, содержащихся в данном множестве. В силу аксиомы объединения такой ординал существует всегда, независимо от размера исходного множества.

Класс всех порядковых чисел не является множеством. В противном случае можно было бы доказать, что такое множество само является порядковым числом и, следовательно, своим собственным элементом, что противоречит строгой -упорядоченности. Это утверждение называется парадоксом Бурали-Форти. Класс порядковых чисел обозначается различными способами: «Ord», «ON», или «∞».

Порядковое число конечно тогда и только тогда, когда оно вполне упорядочено не только естественным, но и противоположным порядком — это условие выполняется в том и только в том случае, когда каждое из его подмножеств содержит наибольший элемент.

Другие варианты определений

В современной математике существуют и другие подходы к определению порядковых чисел. Так, при выполнении аксиомы регулярности следующие утверждения относительно множества x являются эквивалентными:

• x — порядковое число,
• x — транзитивное множество с трихотомичным отношением
• x — транзитивное множество, линейно упорядоченное отношением . Для множества определим двуместное отношение , состоящее из таких пар , что или . Множество называется транзитивным, если из следует . Множество называется ординалом, если оно транзитивно и — вполне упорядоченное множество.
• x — транзитивное множество, элементы которого также являются транзитивными множествами.

Перечисленные определения неприменимы в теориях множеств без аксиомы фундирования. В теориях с урэлементами определения необходимо уточнить, поскольку урэлементы из числа элементов порядкового числа.

Трансфинитная последовательность

Если — предельный ординал, а — некоторое множество, то -индексированной последовательностью элементов называется функция из в . Введенное таким образом определение трансфинитной последовательности или последовательности, индексированной ординалами, является обобщением понятия последовательности. Обычная последовательность соответствует случаю .

Свойства

• Если — порядковое число, то каждый элемент — порядковое число.
• Для любых выполняется ровно одно из следующих соотношений:
• Любое множество порядковых чисел вполне упорядочено отношением (в частности, любое порядковое число, рассматриваемое как множество, вполне упорядочено отношением ), при этом — наименьший элемент множества , — порядковое число, большее или равное любому из элементов множества . Выражения и для порядковых чисел эквивалентны. Ниже подразумевается, что порядковые числа сравниваются с помощью отношения
• Для любого вполне упорядоченного множества существует единственное порядковое число, изоморфное (в частности, для любого множества порядковых чисел существует единственное порядковое число, изоморфное ему).
• Любое совпадает с множеством всех порядковых чисел, меньших, чем .
• Начальный сегмент любого порядкового числа является порядковым числом.
• Пустое множество — наименьшее порядковое число (а значит, оно является элементом любого другого порядкового числа).
• называется непредельным, если либо оно равно , либо существует непосредственно предшествующее ему другими словами, если существует но между ними нельзя вставить другое порядковое число В последнем случае говорят, что — порядковое число, следующее за , и пишут: (иногда просто что оказывается согласованным с обозначением для суммы порядковых чисел).
• Порядковые числа, не являющиеся непредельными, называются предельными порядковыми числами (иногда тоже относят к предельным порядковым числам).
• 
• Множество всех конечных порядковых чисел изоморфно множеству неотрицательных целых чисел, и для них используются такие же обозначения, как для целых чисел. При этом операции сложения, умножения и возведения в степень для порядковых чисел переходят в соответствующие операции для целых чисел. Несколько первых порядковых чисел:

• Множество всех конечных порядковых чисел обозначается Оно является наименьшим предельным порядковым числом и наименьшим бесконечным (а именно счетным) порядковым числом. Следующим за ним порядковым числом является
• Условие конечности можно записать как или, что то же самое,
• Существует бесконечное множество порядковых чисел, но не существует множества всех порядковых чисел. Иначе говоря, совокупность всех порядковых чисел является собственно классом.
• Каждое множество порядковых чисел ограничено сверху и имеет точную верхнюю грань, которая обозначается При этом
• Если — предельное порядковое число или , то иначе
• Точная верхняя грань счетного множества счетных порядковых чисел счетна .
• Каждое порядковое число α имеет единственное представление в нормальной форме Кантора (англ.) , где , , и порядковые числа. Форма позволяет находить разложения подобные следующему:

Арифметика порядковых чисел

Определения операций

• Сумма порядковых чисел рекурсивно определяется следующим образом:

где третье правило применяется в случае, когда является предельным порядковым числом.

• Используя те же обозначения, определим операцию умножения:

• Используя те же обозначения, определим операцию возведения в степень:

Свойства операций

• Сложение порядковых чисел некоммутативно; в частности,
• Сложение порядковых чисел ассоциативно: что позволяет записывать сумму нескольких слагаемых без скобок.
• Сумма возрастает при росте правого слагаемого и не убывает при росте левого слагаемого: из следует и
• Если то существует единственный ординал , для которого
• Умножение порядковых чисел некоммутативно; в частности,
• Умножение порядковых чисел ассоциативно: что позволяет записывать произведение нескольких сомножителей без скобок.
• Для сложения и умножения выполняется левая дистрибутивность:
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• В случае конечности аргументов сложение, умножение и возведение в степень переходят в соответствующие операции для целых чисел (с конечными результатами).
• В случае счетности аргументов результаты сложения, умножения и возведения в степень также являются счетными.

Вау!! 😲 Ты еще не читал? Это зря!

• Кардинальное число
• ТРАНСФИНИТНОЕ ЧИСЛО