Лекция
Привет, Вы узнаете о том , что такое вероятностная комбинаторика, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое вероятностная комбинаторика, случайные подстановки, подстановки в комбинаторика , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
вероятностная комбинаторика , раздел дискретной математики, в котором методы теории вероятностей применяются для изучения комбинаторных объектов. В вероятностной комбинаторики рассматриваются также перечислительные задачи комбинаторики и вопросы существования комбинаторных объектов с заданными характеристиками.
Этот раздел отвечает на вопросы вида: какова вероятность присутствия определенного свойства для случайного дискретного объекта, такого как случайный граф? Например, каково среднее число треугольников в случайном графе? Вероятностные методы также используются для определения существования комбинаторных объектов с определенными заданными свойствами (для которых явные примеры может быть трудно найти), просто наблюдая, что вероятность случайного выбора объекта с этими свойствами больше 0. Этот подход (часто называемый вероятностным методом) доказал свою высокую эффективность в приложениях экстремальной комбинаторики и теории графов. Тесно связанной областью является изучение конечных цепей Маркова, особенно на комбинаторных объектах. Здесь снова используются вероятностные инструменты для оценки времени смешивания.
Часто ассоциируемая с Палом Эрдешем, который сделал новаторскую работу по этому предмету, вероятностная комбинаторика традиционно рассматривалась как набор инструментов для изучения задач в других частях комбинаторики. Однако с ростом приложений для анализа алгоритмов в информатике, а также классической теории вероятностей, аддитивной теории чисел и вероятностной теории чисел, эта область в последнее время выросла и стала самостоятельной областью комбинаторики.
При использовании вероятностных методов для решения перечислительных задач комбинаторики на конечном множестве комбинаторных объектов задается вероятностное распределение и исследуются распределения характеристик случайного комбинаторного объекта из этого множества. Если заданное распределение является равномерным, то вероятность того, что некоторая характеристика случайного объекта приняла какое-то значение, есть отношение числа объектов, обладающих этим значением характеристики, к общему числу объектов в множестве, так что, если общее число объектов известно, задача нахождения вероятности и перечислительная задача нахождения числа объектов с заданным значением характеристики эквивалентны.
Первые шаги вероятностной комбинаторики связаны с развитием в сер. 17 в. элементарной теории вероятностей, когда комбинаторные методы использовались для подсчета разл. вероятностей в азартных играх. Первые результаты исследований в вероятностной комбинаторики с использованием совр. методов теории вероятностей появились в работах В. Л. Гончарова 1942–44, в которых получены осн. результаты о предельном поведении случайных величин, связанных с цикловой структурой случайных подстановок при возрастании их степеней. Случайная подстановка в комбинаторике степени n – это подстановка, выбираемая с равными вероятностями из множества всех подстановок степени n. С использованием хорошо развитых в теории вероятностей методов доказательства предельных теорем (метода производящих функций, метода характеристических функций, а также метода моментов) Гончаровым было доказано, что число циклов длины r в случайной подстановке степени n имеет в пределе при n→∞ распределение Пуассона с параметром 1/r, распределение общего числа циклов сближается с нормальным распределением с параметрами (lnn,lnn ), найдено предельное распределение макс. Об этом говорит сайт https://intellect.icu . длины цикла случайной подстановки. Впоследствии эти результаты во многом служили образцом для изучения разл. классов случайных комбинаторных объектов, в т. ч. случайных размещений, случайных разбиений целых чисел на целочисленные слагаемые, разл. классов случайных графов (случайных отображений, лесов, деревьев), случайных матриц, систем случайных уравнений, случайных автоматов, случайных алгоритмов.
При изучении случайных графов венг. математиками П. Эрдешем и А. Реньи был обнаружен (1960) неожиданный эффект, который по аналогии с подобным эффектом в поведении систем частиц в статистич. физике трактуется как фазовый переход. Пусть 𝒢n,T – случайный граф с n вершинами, который получается в результате размещения T ребер, каждое из которых независимо от размещения остальных ребер занимает любое из n(n−1)/2 возможных мест с равными вероятностями. Пусть 2T/n→λ при n,T→∞ . Если λ<1, точнее, если ( 1–2T/n)3n→∞, то граф 𝒢n,T с вероятностью, стремящейся к единице, состоит из связных компонент, которые являются либо деревьями, либо компонентами, содержащими ровно один цикл. При переходе параметром 2T/n значения 1, точнее, в области, где при n,T→∞ параметр (1–2T/n)3 стремится к к.-л. постоянной c, появляется т. н. гигантская компонента, число вершин в которой асимптотически нормально с математич. ожиданием α(c)n, при этом с убыванием параметра c параметр α(c) возрастает. При (1–2T/n)3n→–∞ граф 𝒢n,T с вероятностью, стремящейся к единице, состоит из гигантской компоненты, деревьев и компонент с одним циклом. Такое поведение случайного графа при переходе параметром 2T/n значения 1 можно интерпретировать как фазовый переход или, другими словами, как наличие порогового эффекта в поведении случайного графа. Позднее пороговый эффект был обнаружен в поведении еще более простых случайных комбинаторных объектов таких, как случайные леса из корневых и некорневых деревьев.
Вероятностный подход используется и для доказательства существования комбинаторных объектов без привлечения конструктивных построений. Простейший вариант этого подхода основан на том, что если математич. ожидание целочисленной неотрицательной случайной величины положительно, то эта случайная величина не равна тождественно нулю. Один из примеров применения вероятностного подхода состоит в следующем.
Пусть 𝒢n(p) – случайный граф с n вершинами, в котором каждая пара вершин независимо от остальных соединена ребром с вероятностью p (с вероятностью q такого ребра нет, p+q=1). В графе
, дополнительном к графу 𝒢n(p), пара вершин соединена ребром тогда и только тогда, когда такого ребра нет в 𝒢n(p) . Пусть vn(p,k) и 
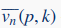– числа полных подграфов с k вершинами в 
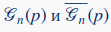соответственно.
Для математическихожиданий справедливы равенства
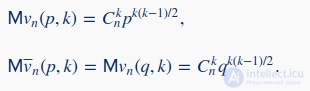
Если число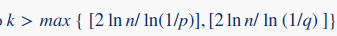 
, где
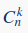– биномиальные коэффициенты,
[a] – целая часть числа a, то и при n→∞.
Следствием этих соотношений является то, что для каждого фиксированного p,0 n существует граф Gn(p) c n вершинами, не содержащий полного подграфа с более чем 2lnn/ln(1/p) вершинами, дополнительный граф G¯n(p) которого не содержит полного подграфа с более чем lnn/ln(1/q) вершинами.
Значительное внимание в вероятностной комбинаторики уделяется генерации последовательностей случайных чисел, генерации случайных комбинаторных объектов таких, как случайные подстановки, а также вероятностному анализу алгоритмов и построению вероятностных алгоритмов, включающих в себя датчики случайных чисел.
Исследование, описанное в статье про вероятностная комбинаторика, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое вероятностная комбинаторика, случайные подстановки, подстановки в комбинаторика и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.