Лекция
Привет, сегодня поговорим про применение раскраски графов, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое применение раскраски графов , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
Раскраска графов практически применяется (постановка задачи различных раскрасок здесь обсуждаться не будет) для:
минимальным числом красок
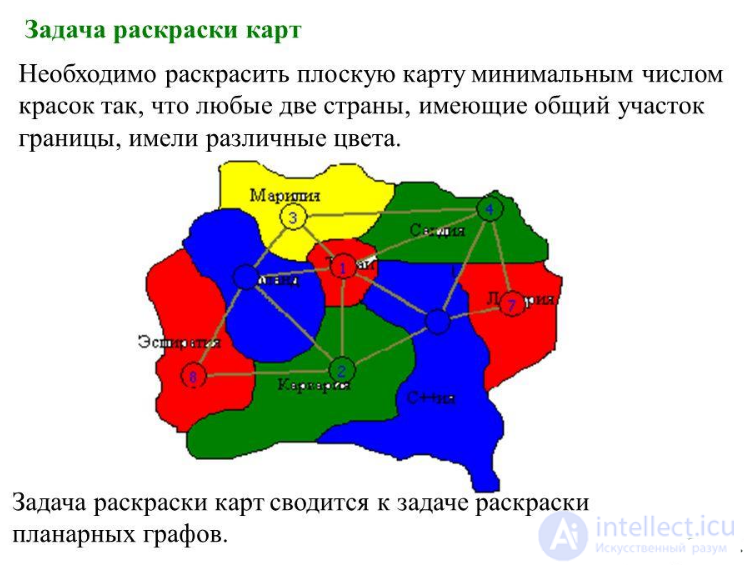
Задача раскраски карт Задача раскраски карт сводится к задаче раскраски планарных графов. Необходимо раскрасить плоскую карту минимальным числом красок так, что любые две страны, имеющие общий участок границы, имели различные цвета.
Теорема. Для оптимальной раскраски планарных графов достаточно четырех цветов. (1977, K. Appel, W. Haken, J. Koch) Решение путем сведения к задаче о кратчайшем покрытии. Данная задача сводится к поиску минимального числа максимальных пустых подграфов, которые в своей совокупности содержат все вершины заданного графа. Утверждение. Вершины, которые не принадлежат пустому подграфу, должны покрывать все ребра заданного графа (действительно, иначе обе вершины непокрытого ребра должны принадлежать этому подграфу, что невозможно). На основании приведенного утверждениия построение пустого подграфа можно свести к поиску подмножества вершин покрывающего все ребра заданного графа.
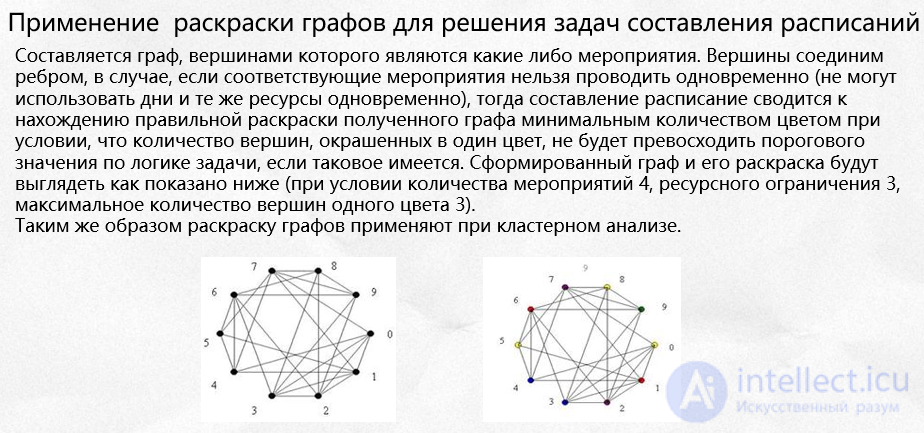
Вероятно, любому конкретному виду раскраски найдется применение в составлении расписаний.
См. : Распределение регистров
Заметную роль в быстродействии программ на компьютере играет время обращения микропроцессора к данным. А именно, процессор может обращаться (перечислим устройства в порядке убывания быстродействия и увеличения объема) к:
Далее, рассмотрим оптимизации программ, связанные с распределением данных в этих устройствах.
Первыми важными работами, заложившими основы применения метода раскраски графов в распределении регистров, были , — последующие же не добавили ничего революционного, внимание в них было сконцентрировано на ускорении работы алгоритма, уменьшении памяти, новых эвристиках по определению стоимостиоткачки регистров (введем определение далее) и выбору регистров для откачки; обзор этих методов можно найти в .
Далее, рассмотрим способ, предложенный в .
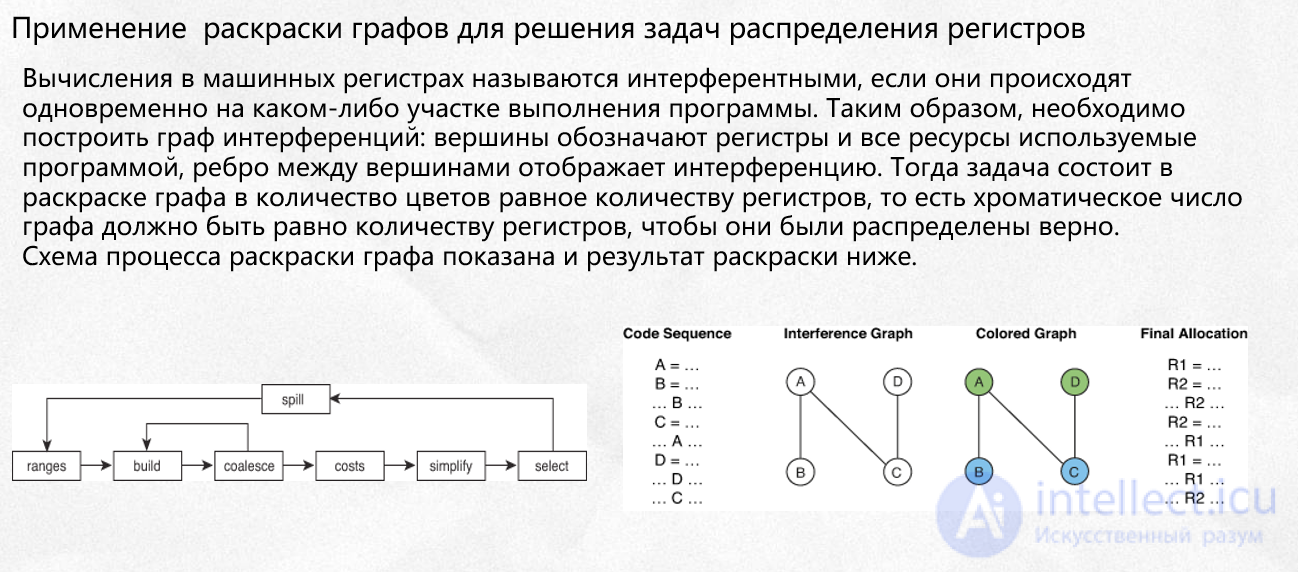
Распределение регистров (англ. register allocation) микропроцессора обычно производится на этапе компиляции.
На вход процедуры распределения подается некий внутренний код (англ. IL, intermediate language, internal language), который рассчитан на виртуальную машину с неограниченным числом регистров — будем называть их виртуальными регистрами.
На выходе процедуры обращения к виртуальнам регистрам переводятся либо в обращения к реальным регистрам процессора, либо, если первого нельзя сделать по причине того, что все регистры уже заняты, — в обращения к оперативной памяти путем введения дополнительного кода. Этот код называют кодом откачки (англ. spillcode), а сам процесс — откачкой (spilling). Отметим, что при обращении к оперативной памяти так же иногда используются реальные регистры (для тех команд процессора, которые в качестве аргумента не могут принимать адрес в памяти).
Для примера, количество регистров общего назначения в большей части процессоров Intel, соответствующих архитектуре:
(Однако, даже не все из них могут быть использованы в нашей процедуре распределения регистров, поскольку уже могут быть заняты — но это уже тонкие вопросы реализации.) Оперативная память же можеть хранить очень большое число «откачанных» «регистров» — ограничения на ее объем рассматривать не будем.
Перед выполнением самой процедуры распределения, стоит сделать:
Сам алгоритм распределения регистров состоит из следующих шагов:
Практика показывает, что алгоритм сходится довольно быстро.
Раскраска графа применяется во многих известных компиляторах, например:
Процессоры, способные одновременно и независимо выполнять несколько команд, находят все более широкое применение; о них говорят, что те поддерживаютпараллелизм на уровне команд (англ. Об этом говорит сайт https://intellect.icu . Instruction-level parallelism, ILP). Назовем их ILP-процессорами. Класс ILP-процессоров включает в том числе процессоры с очень длинным командным словом - VLIW (Very Large Instruction Word, к числу которых относятся, в частности, многие модели цифровых процессоров обработки сигналов (ЦПОС). Самой известной коммерчески успешной реализацией концепции параллелизма на уровне отдельных инструкций является семейство микропроцессоров Itanium компании Intel. Также стоит отметить архитектуру E2K, разработанную российской компанией МЦСТ.
Для реального использования высокой производительности ILP-процессоров необходимы компиляторы языков высокого уровня, способные генерировать эффективный код; в том числе, важна и оптимизация распределения регистров. Введение ILP требует серьезной переработки метода Хайтина в части построения графа несовместимости; в предложен доработанный вариант.
Был предложен также и алгоритм для распределения часто используемых областей кода в кэше[10] — т. н. англ. cache line coloring.
Граф несовместимости здесь такой: вершины — некие «блоки» кода (можно, например, брать процедуры), ребра существуют тогда, когда из одного «блока» ввызывается другой. Как видно, мы концентрируемся на т. н. конфликтах первого поколения (first-generation cache conflicts) — между «блоком» и ее вызывающим/вызываемым. Но стоит отметить, что задача раскраски решается не алгоритмами общего назначения, а специальным эвристическим, который, к тому же, дает решение, которое удовлетворяет неким дополнительным условиям.
Достоинство этого метода — в том, что учитываются и размеры кэша, строки кэша, «блоков» кода, и ассоциативность кэша. Метод удачно комбинируется с другими оптимизациями и inline-функциями[10][11]. Надо отметить, что он может реализовываться оптимизатором — но не оптимизатором компилятора, а оптимизаторомкомпоновщика.
(англ. Spectrum management, англ. frequency allocation)
Хорошей работой, классифицирующей такие задачи и систематически излагающей их решения, является [12].
Термин «распределение частот» объединяет разные типы задач, которые зачастую имеют разные цели и модели. Эти задачи включают в себя:
Общее между задачами — это то, что они все производят оптимальное распределение ограниченного набора ресурсов радиоспектра между пользователями, количество коих в современных условиях все время растет.
Два основных направления оптимизации тут:
В ходе рассмотрения подходящих моделей, в [12] возникают задачи не намного сложнее T-раскраски (англ. T-coloring) мультиграфа, списочной T-раскраски (англ. set T-coloring).
Как пример работы над реальной сотовой сетью, результаты коей были далее применены оператором в своей практической деятельности — [13] (Проведено оператором E-Plus ( (англ.) en:E-Plus) — 3-м по величине в Германии (на 2010)).

Обобщенно представим задачу так: объекты — некие вычисления, между которыми надо разделить вычислительные ресурсы (процессоры, компьютеры…), могущие работать параллельно друг другу. Какие-то вычисления могут выполняться в параллели друг другу, какие-то — нет. Соответственно, вершинная раскраска графа несовместимости вычислений и представляет собой искомое распределение.
Приведем следующие примеры численных методов, которые таким образом можно распараллелить:
Разложение Холецкого для метода сопряженных градиентов с предопределением
Вау!! 😲 Ты еще не читал? Это зря!: en:Conjugate gradient method#The preconditioned conjugate gradient method
[14] Этот метод является одним из лучших итерационных методов для решения систем линейных алгебраических уравнений (СЛАУ) с большими, разреженными,симметричными, положительно определенными матрицами.
Метод Гаусса—Зейделя в применении к разреженным матрицам
Тоже итерационный метод решения СЛАУ.
Этот, в свою очередь, хорош, например, для расчета энергораспределительных электросетей: такие сети могут быть представлены графами, вершины которых — это потребители и источники электроэнергии, а ребра — линии электропередач; далее, строится СЛАУ, в матрице которой диагональным элементам соответствуют узлы вышеупомянутого графа, а ненулевым недиагональным — ребра.[15]
Также, метод может служить т.н. сглаживателем (англ. iterative smoother) для многосеточных методов решения задач методом конечных элементов. (англ. multigrid methods of finite element problems). Оптимизация метода Гаусса—Зейделя, используемого в сглаживании, с помощью т.н. англ. sparse tiling для такого случая его использования рассмотрена в [16].
Методы с использованием адаптивно уточняемой сетки
(англ. Adaptive mesh refinement)
[17] Они, в свою очередь , полезны в решении дифференциальных уравнений в частных производных (ДУЧП). Принцип уточнения здесь такой: в местах, где ожидается наибольшая локальная погрешность — где решение меняется быстрее всего, плотность сетки выбирается большей.
Метод координатной релаксации
(англ. Method of coordinate relaxation)
[18] Удачно применяется в нахождении экстремальных собственных значений очень больших разреженных симметричных матриц. Иногда таких больших, что их практичнее генерировать на лету, чем хранить в памяти. Такие задачи часто встают в квантовой механике.
Предопределение неполным LU-разложением
(Preconditioning by ILU, Incomplete LU-factorization)
Для решения СЛАУ с использованием подпространств Крылова.[19]
Вычисление матриц производных (якобианов и гессианов) в том случае, когда они разреженные, можно серьезно ускорить с помощью раскраски графов. Существует проект «Graph Coloring for Computer Derivatives», сайт — [www 3]. На сайте представлены публикации по теме, а также — программный пакет, в который оформили участники проекта свои достижения. Для введения в предмет можно посмотреть, одну из презентаций, относящихся к проекту, — [20].
Для простого случая, когда «уплотнение» производной ограничивается уменьшением количества столбцов, приведем алгоритм :
Вход: функция от вектора — 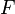
Выход: производная 1. Исследуем структуру разреженности производной 2. Составим матрицу 3. Вычислим значения уплотненной 4. И теперь, восстановим значения |
Место раскраски графа здесь — в вычислении  . В простых случаях надо вычислять обычную вершинную (англ. distance-1); distance-2 раскраску (которая, в том числе сводится к distance-1 раскраске square graph); в более сложных, требуются небольшие дополнительные ограничения:
. В простых случаях надо вычислять обычную вершинную (англ. distance-1); distance-2 раскраску (которая, в том числе сводится к distance-1 раскраске square graph); в более сложных, требуются небольшие дополнительные ограничения:
В рамках вышеуказанного проекта были проведены вычисления для технических производственных задач:
Электронные водяные знаки наносятся на программное обеспечение с целью защиты
интеллектуальной собственности. Суть их состоит не в добавлении какого либо кода в программу, а в переводе подписи автора в множество дополнительных ограничений, которые добавляются в
оригинал ПО. Так как такая подпись основана на добавлении ограничений, то возможно некоторое ухудшение качества самого ПО. Поэтому необходимо держать баланс между степенью надежности защиты и степенью снижения качества ПО.
Раскраска графов применяется в так называемой constraint-based (основанной на ограничениях)
технологии нанесения электронного водяного знака. Исследования показали, что даже огромный
объем информации водяного знака может быть внедрен в граф, и при этом хроматическое число
графа, с водяным знаком будет отличаться не более, чем на 1. И даже практически все графы с
большим дополнительным объемом информации о водяном знаке могут быть раскрашены в
известное число цветов оригинального графа, без увеличения временных затрат.
Далее будут изложены три различных подхода к кодированию электронной подписи с помощью
алгоритмов раскраски графа.
Технология цифровых водяных знаков (англ. digital watermarking) позволяет вместе с данными (будь то медиафайлы, исполняемые файлы и прочие) передать некое скрытое сообщение («водяной знак», Watermark). Такое скрытое сообщение может быть применено в защите авторских прав для идентификации владельца данных.
Это важно, например, для установления источника их распространения нелегальным образом. Или же для подтверждения прав на данные , например — программное обеспечение систем на кристалле (system-on-chip).
Сообщение можно закодировать в том числе и в графе. Одну из таких техник предложили Qu и Potkonjak (поэтому ее иногда называют QP-алгоритмом) в [21].
Состоит она вот в чем: допустим, у нас есть граф G, раскраска которого используется в программе — причем, используется так, что допустимо поменять содержимое графа с небольшим увеличением его хроматического числа. Что важно, одним из таких примеров является граф несовместимости распределения регистров процессора, о котором говорилось выше, — а значит, мы сможем закодировать послание в программном продукте с помощью распределения регистров.
Извлечь его можно путем сравнения полученного графа с исходным; существуют и способы удостовериться в том, было ли некое сообщение закодировано в графе без использования исходного — подробнее извлечение описано, например, в [22].
Развитие и уточнение мыслей Qu и Potkonjak, попытки улучшения алгоритма происходит в работах [23], [24], [22].
Отметим, что в [23], [24] есть ссылки на программный пакет SandMark, в котором исполнены алгоритмы такого рода; доступен для скачивания на [www 4].

 и
и  проводим тогда и только тогда, когда:
проводим тогда и только тогда, когда:
 , или,
, или, , или,
, или,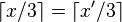 и
и  .
.Надеюсь, эта статья про применение раскраски графов, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое применение раскраски графов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.