Кластерный анализ - как упорядочивающая операция объектов в однородные группы

Привет, Вы узнаете о том , что такое кластерный анализ, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое кластерный анализ , настоятельно рекомендую прочитать все из категории Интеллектуальный анализ данных.

кластерный анализ (англ. cluster analysis) — многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы Задача кластеризации относится к статистической обработке, а также к широкому классу задач обучения без учителя.

Большинство исследователей (см., напр., ) склоняются к тому, что впервые термин «кластерный анализ» (англ. cluster — гроздь, сгусток, пучок) был предложен математиком Р. Трионом . Впоследствии возник ряд терминов, которые в настоящее время принято считать синонимами термина «кластерный анализ»: автоматическая классификация, ботриология.

Спектр применений кластерного анализа очень широк: его используют в археологии, медицине, психологии, химии, биологии, государственном управлении, филологии, антропологии, маркетинге, социологии, геологии и других дисциплинах. Однако универсальность применения привела к появлению большого количества несовместимых терминов, методов и подходов, затрудняющих однозначное использование и непротиворечивую интерпретацию кластерного анализа.

КЛАСТЕРНЫЙ АНАЛИЗ

Задачи и условия кластерного анализа

Кластерный анализ выполняет следующие основные задачи:

• Разработка типологии или классификации.
• Исследование полезных концептуальных схем группирования объектов.
• Порождение гипотез на основе исследования данных.
• Проверка гипотез или исследования для определения, действительно ли типы (группы), выделенные тем или иным способом, присутствуют в имеющихся данных.

Независимо от предмета изучения применение кластерного анализа предполагает следующие этапы:

• Отбор выборки для кластеризации. Подразумевается, что имеет смысл кластеризовать только количественные данные.
• Определение множества переменных, по которым будут оцениваться объекты в выборке, то есть признакового пространства.
• Вычисление значений той или иной меры сходства (или различия) между объектами.
• Применение метода кластерного анализа для создания групп сходных объектов.
• Проверка достоверности результатов кластерного решения.

Можно встретить описание двух фундаментальных требований, предъявляемых к данным — однородность и полнота. Однородность требует, чтобы все кластеризуемые сущности были одной природы, описывались сходным набором характеристик . Если кластерному анализу предшествует факторный анализ, то выборка не нуждается в «ремонте» — изложенные требования выполняются автоматически самой процедурой факторного моделирования (есть еще одно достоинство — z-стандартизация без негативных последствий для выборки; если ее проводить непосредственно для кластерного анализа, она может повлечь за собой уменьшение четкости разделения групп). В противном случае выборку нужно корректировать.

Типология задач кластеризации

Типы входных данных

• Признаковое описание объектов. Каждый объект описывается набором своих характеристик, называемых признаками. Признаки могут быть числовыми или нечисловыми.
• Матрица расстояний между объектами. Каждый объект описывается расстояниями до всех остальных объектов метрического пространства.
• Матрица сходства между объектами . Учитывается степень сходства объекта с другими объектами выборки в метрическом пространстве. Сходство здесь дополняет расстояние (различие) между объектами до 1.

В современной науке применяется несколько алгоритмов обработки входных данных. Анализ путем сравнения объектов, исходя из признаков, (наиболее распространенный в биологических науках) называется Q-типом анализа, а в случае сравнения признаков, на основе объектов — R-типом анализа. Существуют попытки использования гибридных типов анализа (например, RQ-анализ), но данная методология еще должным образом не разработана.

Цели кластеризации

• Понимание данных путем выявления кластерной структуры. Разбиение выборки на группы схожих объектов позволяет упростить дальнейшую обработку данных и принятия решений, применяя к каждому кластеру свой метод анализа (стратегия «разделяй и властвуй»).
• Сжатие данных. Если исходная выборка избыточно большая, то можно сократить ее, оставив по одному наиболее типичному представителю от каждого кластера.
• Обнаружение новизны (англ. novelty detection). Выделяются нетипичные объекты, которые не удается присоединить ни к одному из кластеров.

В первом случае число кластеров стараются сделать поменьше. Во втором случае важнее обеспечить высокую степень сходства объектов внутри каждого кластера, а кластеров может быть сколько угодно. В третьем случае наибольший интерес представляют отдельные объекты, не вписывающиеся ни в один из кластеров.

Во всех этих случаях может применяться иерархическая кластеризация, когда крупные кластеры дробятся на более мелкие, те в свою очередь дробятся еще мельче, и т. д. Такие задачи называются задачами таксономии. Результатом таксономии является древообразная иерархическая структура. При этом каждый объект характеризуется перечислением всех кластеров, которым он принадлежит, обычно от крупного к мелкому.

Методы кластеризации

Общепринятой классификации методов кластеризации не существует, но можно выделить ряд групп подходов (некоторые методы можно отнести сразу к нескольким группам и потому предлагается рассматривать данную типизацию как некоторое приближение к реальной классификации методов кластеризации) :

1. Вероятностный подход. Предполагается, что каждый рассматриваемый объект относится к одному из k классов. Некоторые авторы (например, А. И. Орлов) считают, что данная группа вовсе не относится к кластеризации и противопоставляют ее под названием «дискриминация», то есть выбор отнесения объектов к одной из известных групп (обучающих выборок).
   • K-средних
   • К-медиан
   • EM-алгоритм
   • Алгоритмы семейства FOREL
   • Дискриминантный анализ
2. Подходы на основе систем искусственного интеллекта: весьма условная группа, так как методов очень много и методически они весьма различны.
   • Метод нечеткой кластеризации C-средних (C-means)
   • Нейронная сеть Кохонена
   • Генетический алгоритм
3. Логический подход. Построение дендрограммы осуществляется с помощью дерева решений.
4. Теоретико-графовый подход.
   • Графовые алгоритмы кластеризации
5. Иерархический подход. Предполагается наличие вложенных групп (кластеров различного порядка). Алгоритмы в свою очередь подразделяются на агломеративные (объединительные) и дивизивные (разделяющие). По количеству признаков иногда выделяют монотетические и политетические методы классификации.
   • Иерархическая дивизивная кластеризация или таксономия. Об этом говорит сайт https://intellect.icu . Задачи кластеризации рассматриваются в количественной таксономии.
6. Другие методы. Не вошедшие в предыдущие группы.
   • Статистические алгоритмы кластеризации
   • Ансамбль кластеризаторов
   • Алгоритмы семейства KRAB
   • Алгоритм, основанный на методе просеивания
   • DBSCAN и др.

Подходы 4 и 5 иногда объединяют под названием структурного или геометрического подхода, обладающего большей формализованностью понятия близости[10]. Несмотря на значительные различия между перечисленными методами все они опираются на исходную «гипотезу компактности»: в пространстве объектов все близкие объекты должны относиться к одному кластеру, а все различные объекты соответственно должны находиться в различных кластерах.

Основные понятия кластерного анализа

1. Симметрия. Даны два объекта х и у; расстояние между ними удовлетворяет условию d(x,y)=d(y,x) >=0

2 Неравенство треугольника. Даны три объекта x, y, z; расстояния между ними удовлетворяют условию d(x, y) <= d(x, z)+ d(y, z).

3. Различимость нетождественных объектов. Даны два объекта х и у: если d(х, z) ≠ 0, то х ≠ у.

4. Неразличимость идентичных объектов. Для двух идентичных объектов х и х' d(x,x')=0, т.е. расстояние между этими объектами равно нулю.

Пусть w i - i-я группа (класс, кластер) объектов,

N i - число объектов, образующих группу w i,

вектор μ i - среднее арифметическое объектов, входящих в w i

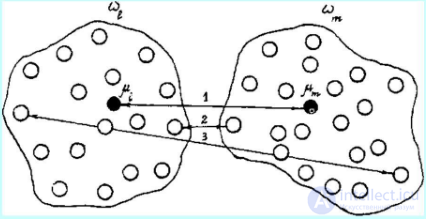
1. Расстояние ближайшего соседа есть расстояние между ближайшими объектами кластеров:

2. Расстояние дальнего соседа расстояние между самыми дальними объектами кластеров:

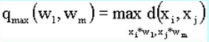
3. Расстояние центров тяжести равно расстоянию между центральными точками кластеров:

4. Обобщенное (по Колмогорову) расстояние между классами, или обобщенное K-расстояние, вычисляется по формуле

МЕРЫ РАССТОЯНИЯ КЛАСТЕРНОГО АНАЛИЗА

1.Евклидово расстояние расстояние (x,y) =

2. Квадрат евклидова расстояния расстояние (x,y) =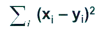

3. Расстояние городских кварталов (манхэттенское расстояние ). расстояние (x,y) =

4. Расстояние Чебышева. расстояние (x,y) =

5. Степенное расстояние. расстояние(x,y) =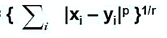

6. Процент несогласия. расстояние(x,y) =

Правила объединения или связи Центроид кластера

• - Одиночная связь (метод ближайшего соседа).
• - Полная связь (метод наиболее удаленных соседей).
• - Невзвешенное попарное среднее.
• - Взвешенное попарное среднее.
• - Невзвешенный центроидный метод.
• - Взвешенный центроидный метод (медиана).
• - Метод Варда.

Формальная постановка задачи кластеризации

Пусть — множество объектов, — множество номеров (имен, меток) кластеров. Задана функция расстояния между объектами . Имеется конечная обучающая выборка объектов . Требуется разбить выборку на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из объектов, близких по метрике , а объекты разных кластеров существенно отличались. При этом каждому объекту приписывается номер кластера .

Алгоритм кластеризации — это функция , которая любому объекту ставит в соответствие номер кластера . Множество в некоторых случаях известно заранее, однако чаще ставится задача определить оптимальное число кластеров, с точки зрения того или иного критерия качества кластеризации.

Кластеризация (обучение без учителя) отличается от классификации (обучения с учителем) тем, что метки исходных объектов изначально не заданы, и даже может быть неизвестно само множество .

Решение задачи кластеризации принципиально неоднозначно, и тому есть несколько причин (как считает ряд авторов):

• не существует однозначно наилучшего критерия качества кластеризации. Известен целый ряд эвристических критериев, а также ряд алгоритмов, не имеющих четко выраженного критерия, но осуществляющих достаточно разумную кластеризацию «по построению». Все они могут давать разные результаты. Следовательно, для определения качества кластеризации требуется эксперт предметной области, который бы мог оценить осмысленность выделения кластеров.
• число кластеров, как правило, неизвестно заранее и устанавливается в соответствии с некоторым субъективным критерием. Это справедливо только для методов дискриминации, так как в методах кластеризации выделение кластеров идет за счет формализованного подхода на основе мер близости.
• результат кластеризации существенно зависит от метрики, выбор которой, как правило, также субъективен и определяется экспертом. Но стоит отметить, что есть ряд рекомендаций к выбору мер близости для различных задач.

АГЛОМЕРАТИВНЫЕ МЕТОДЫ ПОСТРОЕНИЕ ДЕРЕВА РЕШЕНИЙ - ДЕНДРОГРАММЫ

1. Построение матрицы расстояний (меры расстояния)

1-1; 1-2; 1-3; 1-4; ; 1-104; 1-105; 2-1; 2-2; 2-3; 2-4; ; 2-104; 2-105; ; ; 103-1; 103-2; ; ; ; 104-1; 104-2; ; ; ; 105-1; 105-2; ; ;

2 Два наблюдения (монокластера), между которыми самое минимальное расстояние, объединяются в один кластер

3. Анализ оставшихся монокластеров и присоединение нового объекта к существующему кластеру либо объединение двух наблюдений в кластер

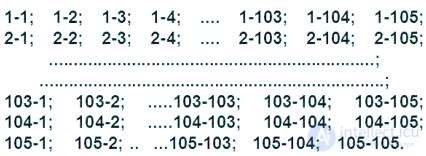
признаки расстояние

Матрица растояний по признакам

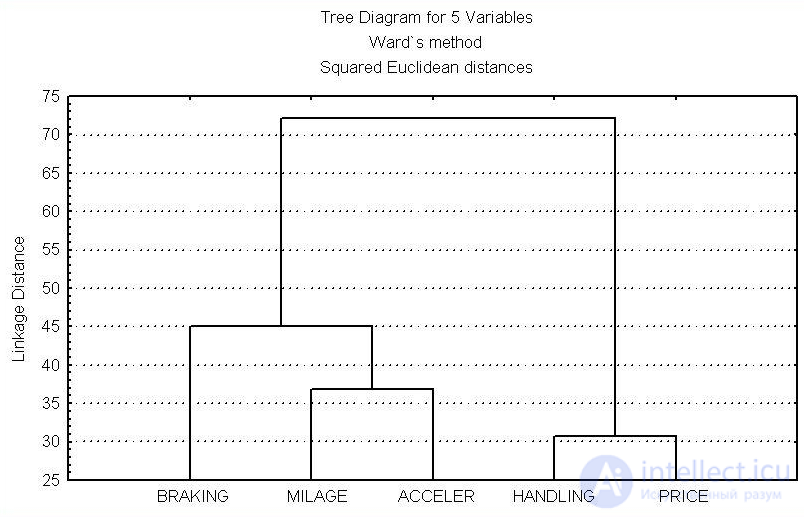
объекты отложены по оси ОХ

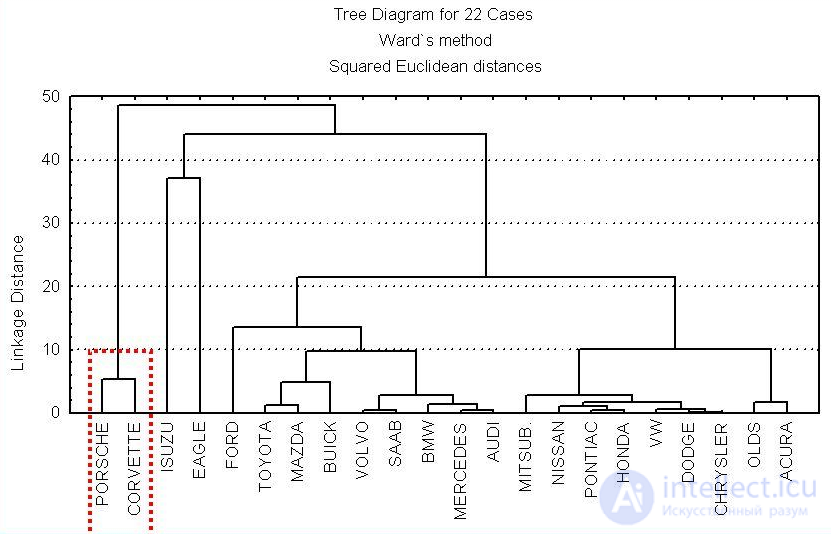
Матрица расстояний

Итерационные методы Метод k-средних Мак-Кина

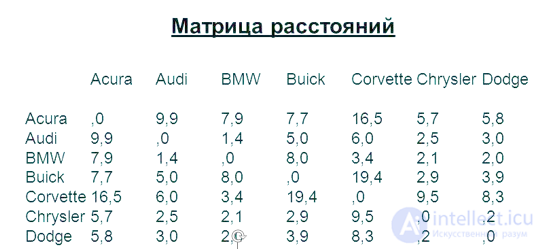
1) выбираются или назначаются k наблюдений, которые будут первичными центрами кластеров;

2) при необходимости формируются промежуточные кластеры;

3) после назначения всех наблюдений отдельным кластерам производится замена первичных кластерных центров на кластерные средние;

4) предыдущая итерация повторяется до тех пор, пока изменения координат кластерных центров не станут минимальными.

1 шаг Назначение объекта – кластером и центроидом

2 шаг Расчет расстояний до всех объектов и объединение с ближайшим объектом в кластер

3 шаг Пересчет центроидов классов

4 шаг Расчет расстояний от центроидов до объектов и объединение с ближайшим объектом в кластер

Шаг 2-4 повторяется итерационно

Шаг N Шаг N+1 Окончательные центроиды Расчет расстояний от центроидов до объектов Перетягивание ближайших объектов, пересчет центроидов Повторение шагов N и N+1 до минимального изменения координат центроидов

Статистики для классов

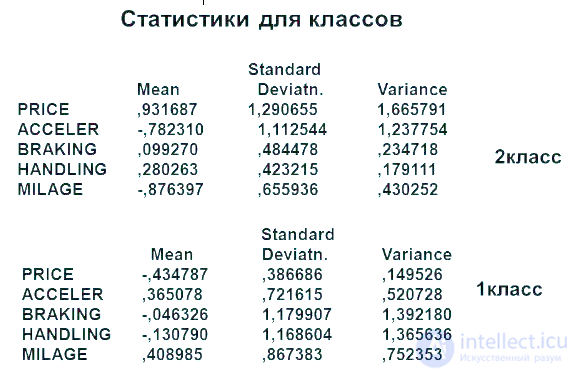
ГРАФИК СРЕДНИХ

22 ПОСЛЕ УДАЛЕНИЯ НЕЗНАЧИМЫХ ПРИЗНАКОВ

Статистики для классов

Применение кластерного анализа

В биологии

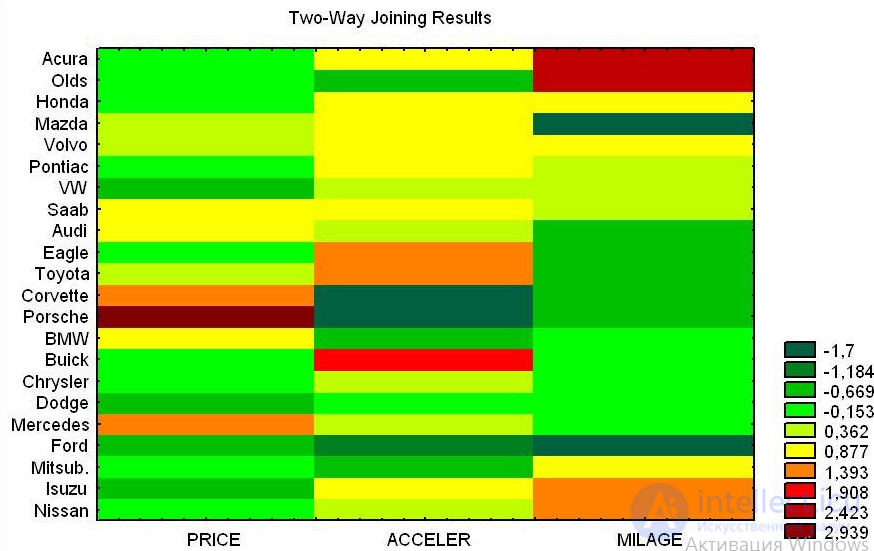
В биологии кластеризация имеет множество приложений в самых разных областях. Например, в биоинформатике с помощью нее анализируются сложные сети взаимодействующих генов, состоящие порой из сотен или даже тысяч элементов. Кластерный анализ позволяет выделить подсети, узкие места, концентраторы и другие скрытые свойства изучаемой системы, что позволяет в конечном счете узнать вклад каждого гена в формирование изучаемого феномена.

В области экологии широко применяется для выделения пространственно однородных групп организмов, сообществ и т. п. Реже методы кластерного анализа применяются для исследования сообществ во времени. Гетерогенность структуры сообществ приводит к возникновению нетривиальных методов кластерного анализа (например, метод Чекановского).

В общем стоит отметить, что исторически сложилось так, что в качестве мер близости в биологии чаще используются меры сходства, а не меры различия (расстояния).

В социологии

При анализе результатов социологических исследований рекомендуется осуществлять анализ методами иерархического агломеративного семейства, а именно методом Уорда, при котором внутри кластеров оптимизируется минимальная дисперсия, в итоге создаются кластеры приблизительно равных размеров. Метод Уорда наиболее удачен для анализа социологических данных. В качестве меры различия лучше квадратичное евклидово расстояние, которое способствует увеличению контрастности кластеров. Главным итогом иерархического кластерного анализа является дендрограмма или «сосульчатая диаграмма». При ее интерпретации исследователи сталкиваются с проблемой того же рода, что и толкование результатов факторного анализа — отсутствием однозначных критериев выделения кластеров. В качестве главных рекомендуется использовать два способа — визуальный анализ дендрограммы и сравнение результатов кластеризации, выполненной различными методами.

Визуальный анализ дендрограммы предполагает «обрезание» дерева на оптимальном уровне сходства элементов выборки. «Виноградную ветвь» (терминология Олдендерфера М. С. и Блэшфилда Р. К.[11]) целесообразно «обрезать» на отметке 5 шкалы Rescaled Distance Cluster Combine, таким образом будет достигнут 80 % уровень сходства. Если выделение кластеров по этой метке затруднено (на ней происходит слияние нескольких мелких кластеров в один крупный), то можно выбрать другую метку. Такая методика предлагается Олдендерфером и Блэшфилдом.

Теперь возникает вопрос устойчивости принятого кластерного решения. По сути, проверка устойчивости кластеризации сводится к проверке ее достоверности. Здесь существует эмпирическое правило — устойчивая типология сохраняется при изменении методов кластеризации. Результаты иерархического кластерного анализа можно проверять итеративным кластерным анализом по методу k-средних. Если сравниваемые классификации групп респондентов имеют долю совпадений более 70 % (более 2/3 совпадений), то кластерное решение принимается.

Проверить адекватность решения, не прибегая к помощи другого вида анализа, нельзя. По крайней мере, в теоретическом плане эта проблема не решена. В классической работе Олдендерфера и Блэшфилда «Кластерный анализ» подробно рассматриваются и в итоге отвергаются дополнительные пять методов проверки устойчивости:

1. кофенетическая корреляция — не рекомендуется и ограничена в использовании;
2. тесты значимости (дисперсионный анализ) — всегда дают значимый результат;
3. методика повторных (случайных) выборок, что, тем не менее, не доказывает обоснованность решения;
4. тесты значимости для внешних признаков пригодны только для повторных измерений;
5. методы Монте-Карло очень сложны и доступны только опытным математикам .

В информатике

• Кластеризация результатов поиска — используется для «интеллектуальной» группировки результатов при поиске файлов, веб-сайтов, других объектов, предоставляя пользователю возможность быстрой навигации, выбора заведомо более релевантного подмножества и исключения заведомо менее релевантного — что может повысить юзабилити интерфейса по сравнению с выводом в виде простого сортированного по релевантности списка.
  • Clusty — кластеризующая поисковая машина компании Vivísimo
  • Nigma — российская поисковая система с автоматической кластеризацией результатов
  • Quintura — визуальная кластеризация в виде облака ключевых слов
• Сегментация изображений (англ. image segmentation) — кластеризация может быть использована для разбиения цифрового изображения на отдельные области с целью обнаружения границ (англ. edge detection) или распознавания объектов.
• Интеллектуальный анализ данных (англ. data mining) — кластеризация в Data Mining приобретает ценность тогда, когда она выступает одним из этапов анализа данных, построения законченного аналитического решения. Аналитику часто легче выделить группы схожих объектов, изучить их особенности и построить для каждой группы отдельную модель, чем создавать одну общую модель для всех данных. Таким приемом постоянно пользуются в маркетинге, выделяя группы клиентов, покупателей, товаров и разрабатывая для каждой из них отдельную стратегию.

Вау!! 😲 Ты еще не читал? Это зря!

• Кластеризация документов
• Классификация документов
• Нейронные сети
• Самоорганизующаяся карта Кохонена
• Кластерный анализ финансовых рынков

Прочтение данной статьи про кластерный анализ позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое кластерный анализ и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Интеллектуальный анализ данных