Лекция
Привет, сегодня поговорим про формула включений-исключений, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое формула включений-исключений, принцип включений-исключений, беспорядок, derangement , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
формула включений-исключений (или принцип включений-исключений ) — комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом. В теории вероятностей аналог принципа включений-исключений известен как формула Пуанкаре .
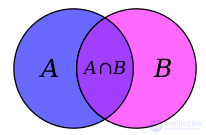
Случай двух множеств
Например, в случае двух множеств 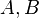 формула включений-исключений имеет вид:
формула включений-исключений имеет вид:
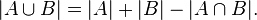
В сумме 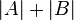 элементы пересечения
элементы пересечения 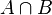 учтены дважды, и чтобы компенсировать это мы вычитаем
учтены дважды, и чтобы компенсировать это мы вычитаем 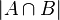 из правой части формулы. Справедливость этого рассуждения видна из диаграммы Эйлера-Венна для двух множеств, приведенной на рисунке справа.
из правой части формулы. Справедливость этого рассуждения видна из диаграммы Эйлера-Венна для двух множеств, приведенной на рисунке справа.
Таким же образом и в случае 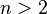 множеств процесс нахождения количества элементов объединения
множеств процесс нахождения количества элементов объединения 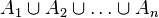 состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы.
состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы.
Формулу включений-исключений можно сформулировать в разных формах.
Пусть 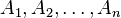 — конечные множества. Формула включений-исключений утверждает:
— конечные множества. Формула включений-исключений утверждает:
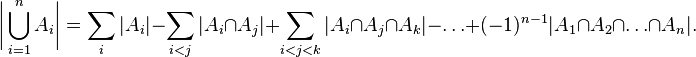
При 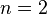 получаем формулу для двух множеств, приведенную выше.
получаем формулу для двух множеств, приведенную выше.
Принцип включений-исключений часто приводят в следующей альтернативной формулировке . Пусть дано конечное множество 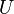 . Тогда имеет место формула:
. Тогда имеет место формула:
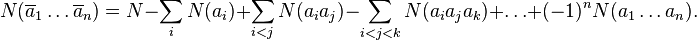
Формулировка принципа включений-исключений в терминах множеств эквивалентна формулировке в терминах свойств. Действительно, если множества 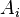 ), и формулу включений-исключений можно переписать так:
), и формулу включений-исключений можно переписать так:
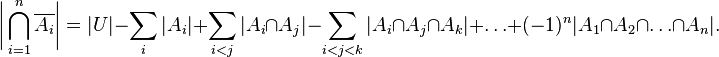
Если теперь вместо «элемент 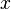 », то мы получим формулировку принципа включений-исключений в терминах свойств, и наоборот.
», то мы получим формулировку принципа включений-исключений в терминах свойств, и наоборот.
Обозначим через 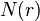 .Тогда формулу включений-исключений можно переписать в следующей замкнутой форме (англ.)
.Тогда формулу включений-исключений можно переписать в следующей замкнутой форме (англ.)
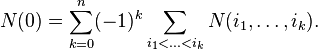
Существует несколько доказательств формулы включений-исключений.
Доказательство по индукции
Формулу включений-исключений можно доказать по индукции .
При 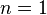 формула включений-исключений тривиальна:
формула включений-исключений тривиальна:
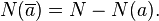
Пусть формула верна для 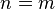 .
.
Пусть каждый элемент множества 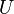 :
:
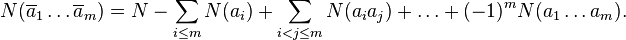
Теперь применим формулу для свойств 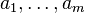 :
:
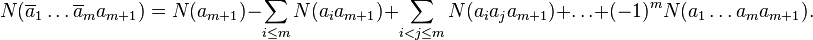
Наконец, применим формулу для одного свойства 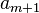 :
:
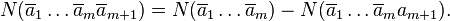
Комбинируя выписанные три формулы, получим формулу включений-исключений для 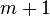 . Что и требовалось доказать. ■
. Что и требовалось доказать. ■
Комбинаторное доказательство
Рассмотрим произвольный элемент 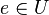 .
.
Если элемент  ).
).
Пусть элемент  в правую часть равен
в правую часть равен
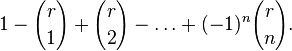
При 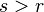 числа сочетаний равны нулю. Оставшаяся сумма в силу биномиальной теоремы равна
числа сочетаний равны нулю. Оставшаяся сумма в силу биномиальной теоремы равна
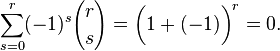
Таким образом, правая часть формулы включений-исключений учитывает каждый элемент, не имеющий указанных свойств точно по одному разу, а каждый элемент, обладающий хотя бы одним из свойств — нуль раз. Следовательно, она равна количеству элементов, не обладающих ни одним из свойств 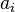 . Что и требовалось доказать. ■
. Что и требовалось доказать. ■
Доказательство через индикаторные функции
Пусть 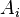 ).
).
Индикаторная функция их дополнений 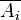 равна
равна
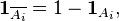
а индикаторная функция пересечения дополнений:
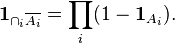
Раскрывая скобки в правой части и еще раз используя тот факт, что индикаторная функция пересечения множеств равна произведению их индикаторных функций, получаем:
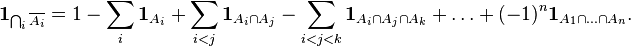
Это соотношение — одна из форм принципа включений-исключений. Оно выражает собой логическое тождество и верно для произвольных множеств 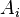 его мощность равна
его мощность равна
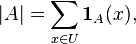
получим формулировку принципа включений-исключений в терминах мощностей множеств (или в терминах свойств). ■
Задача о беспорядках
Классический пример использования формулы включений-исключений — задача о беспорядках . Требуется найти число перестановок 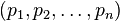 . Такие перестановки называются беспорядками.
. Такие перестановки называются беспорядками.
Пусть 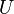 беспорядков:
беспорядков:
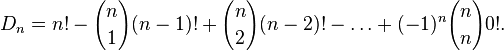
Это соотношение можно преобразовать к виду
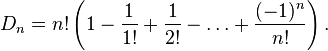
Нетрудно видеть, что выражение в скобках является частичной суммой ряда 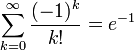 перестановок:
перестановок:
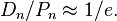
Другой пример применения формулы включений-исключений — нахождение явного выражения для функции Эйлера 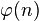 .
.
Пусть каноническое разложение числа 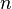 на простые множители имеет вид
на простые множители имеет вид
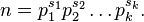
Число 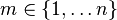 .
.
Количество 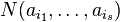 .
.
По формуле включений-исключений находим
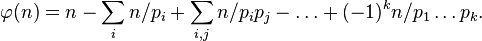
Эта формула преобразуется к виду:
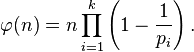
Пусть 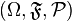
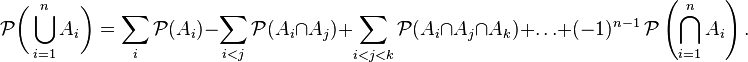
Эта формула выражает принцип включений-исключений для вероятностей. Ее можно получить из принципа включений-исключений в форме индикаторных функций:
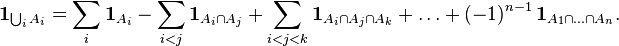
Пусть 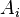 , получим формулу включения-исключения для вероятностей.
, получим формулу включения-исключения для вероятностей.
Пусть 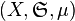 имеет место формула включений-исключений:
имеет место формула включений-исключений:
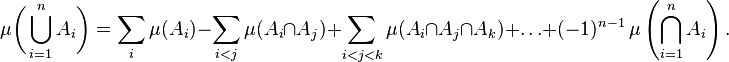
Очевидно, принцип включений-исключений для вероятностей и для мощностей конечных множеств являются частными случаями этой формулы. В первом случае мерой является, естественно, вероятностная мера в соответствующем вероятностном пространстве: 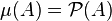 .
.
Вывести принцип включений-исключений для пространств с мерой можно также, как для указанных частных случаев, из тождества для индикаторных функций:
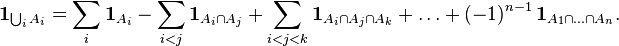
Пусть 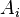 , и получим формулу включений-исключений для меры.
, и получим формулу включений-исключений для меры.
Формула включений-исключений может рассматриваться как частный случай тождества максимумов и минимумов:
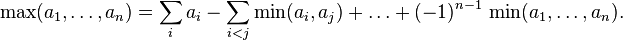
Это соотношение справедливо для произвольных чисел 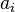 , то получим соотношение для индикаторных функций множеств:
, то получим соотношение для индикаторных функций множеств:
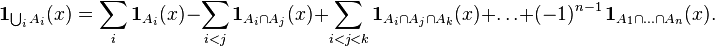
Пусть 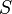 следующим соотношением:
следующим соотношением:
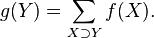
Тогда имеет место следующая формула обращения :
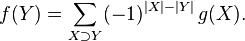
Это утверждение является частным случаем общей формулы обращения Мебиуса для алгебры инцидентности (англ.) совокупности 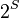 .
.
Покажем, как из этой формулы следует принцип включения-исключения для конечных множеств. Пусть дано семейство подмножеств 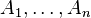 . Математически это можно записать так:
. Математически это можно записать так:
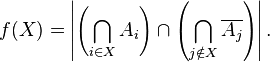
Тогда функция 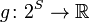 , определенная формулой
, определенная формулой
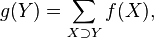
дает количество элементов, каждый из которых входит во все множества 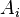 и, быть может, еще в другие. То есть
и, быть может, еще в другие. То есть
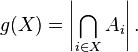
Заметим далее, что 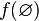 — количество элементов, не обладающих ни одним из свойств:
— количество элементов, не обладающих ни одним из свойств:
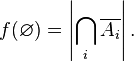
С учетом сделанных замечаний запишем формулу обращения Мебиуса:
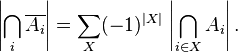
Это есть в точности формула включений-исключений для конечных множеств, только в ней не сгруппированы слагаемые, относящиеся к одинаковым значениям 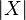 .
.
Впервые формулу включений-исключений опубликовал португальский математик Даниэль да Сильва (англ.) в 1854 году . Об этом говорит сайт https://intellect.icu . Но еще в 1713 году Николай Бернулли использовал этот метод для решения задачи Монмора , известной как задача о встречах (фр. Le problème des rencontres) , частным случаем которой является задача о беспорядках. Также формулу включений-исключений связывают с именами французского математика Абрахама де Муавра и английского математика Джозефа Сильвестра .
Принцип включений-исключений — это важный комбинаторный прием, позволяющий подсчитывать размер каких-либо множеств, или вычислять вероятность сложных событий.
Формулировки принципа включений-исключений
Принцип включений-исключений выглядит следующим образом:
Чтобы посчитать размер объединения нескольких множеств, надо просуммировать размеры этих множеств по отдельности, затем вычесть размеры всех попарных пересечений этих множеств, прибавить обратно размеры пересечений всевозможных троек множеств, вычесть размеры пересечений четверок, и так далее, вплоть до пересечения всех множеств.
В математической форме приведенная выше словесная формулировка выглядит следующим образом:
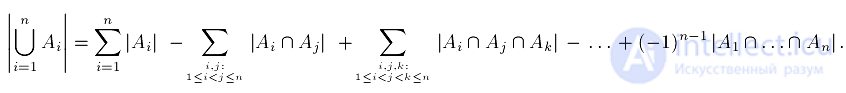
Ее можно записать более компактно, через сумму по подмножествам. Обозначим через 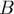 . Тогда принцип включений-исключений принимает вид:
. Тогда принцип включений-исключений принимает вид:
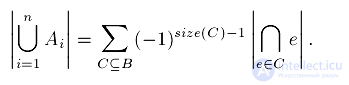
Эту формулу приписывают Муавру (Abraham de Moivre).
Пусть на диаграмме отмечены три фигуры 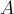 :
:
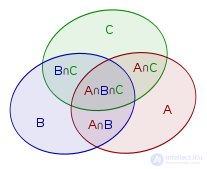
Тогда площадь объединения 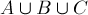 :
:
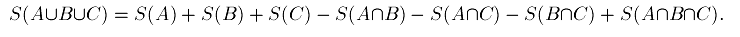
Аналогичным образом это обобщается и на объединение 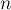 фигур.
фигур.
Если 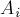 — их вероятности, то вероятность их объединения (т.е. того, что произойдет хотя бы одно из этих событий) равна:
— их вероятности, то вероятность их объединения (т.е. того, что произойдет хотя бы одно из этих событий) равна:
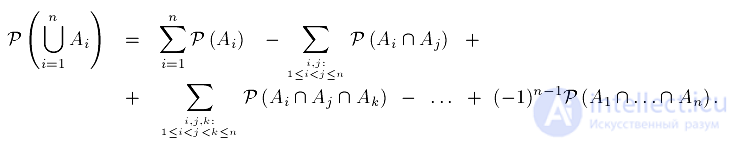
Эту сумму также можно записать в виде суммы по подмножествам множества 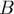 :
:
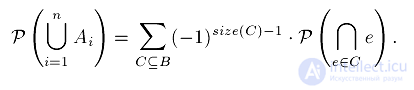
Для доказательства удобно пользоваться математической формулировкой в терминах теории множеств:
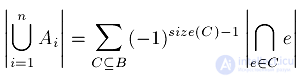
где 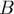 -ых.
-ых.
Нам нужно доказать, что любой элемент, содержащийся хотя бы в одном из множеств 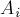 , никак не могут быть учтены, поскольку отсутствуют в правой части формулы).
, никак не могут быть учтены, поскольку отсутствуют в правой части формулы).
Рассмотрим произвольный элемент 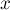 . Покажем, что он посчитается формулой ровно один раз.
. Покажем, что он посчитается формулой ровно один раз.
Заметим, что:
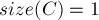 раз, со знаком плюс;
раз, со знаком плюс;
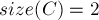 ;
;
 раз, со знаком плюс;
раз, со знаком плюс;

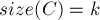 ;
;
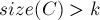 учтется ноль раз.
учтется ноль раз.
Таким образом, нам надо посчитать такую сумму биномиальных коэффициентов:

Проще всего посчитать эту сумму, сравнив ее с разложением в бином Ньютона выражения 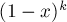 :
:
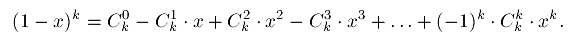
Видно, что при 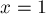 , что и требовалось доказать.
, что и требовалось доказать.
Принцип включений-исключений сложно хорошо понять без изучения примеров его применений.
Сначала мы рассмотрим три простые задачи "на бумажке", иллюстрирующие применение принципа, затем рассмотрим более практические задачи, которые трудно решить без использования принципа включений-исключений.
Особо следует отметить задачу "поиск числа путей", поскольку в ней демонстрируется, что принцип включений-исключений может иногда приводить к полиномиальным решениям, а не обязательно экспоненциальным.
Сколько есть перестановок чисел от 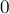 ?
?
Посчитаем число "плохих" перестановок, т.е. таких, у которых первый элемент 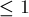 .
.
Обозначим через 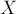
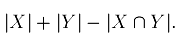
Проведя несложные комбинаторные вычисления, получаем, что это равно:
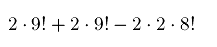
Отнимая это число от общего числа перестановок 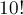 , мы получим ответ.
, мы получим ответ.
Сколько существует последовательностей длины 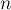 , причем каждое число встречается хотя бы раз?
, причем каждое число встречается хотя бы раз?
Снова перейдем к обратной задаче, т.е. будем считать число последовательностей, в которых не присутствует хотя бы одно из чисел.
Обозначим через 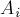
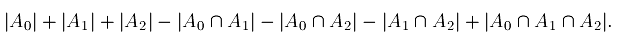
Размеры каждого из 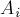 (поскольку доступных цифр вообще не остается).
(поскольку доступных цифр вообще не остается).
Вспоминая, что мы решали обратную задачу, получаем итоговый ответ:
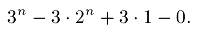
Дано уравнение:
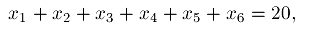
где все 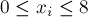 ).
).
Требуется посчитать число решений этого уравнения.
Забудем сначала про ограничение 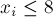 местам:
местам:
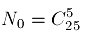
Посчитаем теперь по формуле включений-исключений число "плохих" решений, т.е. таких решений уравнения, в которых один или более 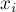 .
.
Обозначим через  элементов исключены из рассмотрения и точно принадлежат первой группе. Таким образом:
элементов исключены из рассмотрения и точно принадлежат первой группе. Таким образом:
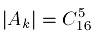
Аналогично, мощность пересечения двух множеств  равна числу:
равна числу:
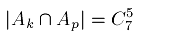
Мощность каждого пересечения трех и более множеств равна нулю, поскольку 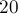 .
.
Объединяя все это в формулу включений-исключений и учитывая, что мы решали обратную задачу, окончательно получаем ответ:
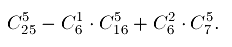
Пусть даны числа 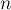 .
.
Сразу перейдем к обратной задаче — посчитаем количество не взаимно простых чисел.
Рассмотрим все простые делители числа 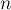 ).
).
Сколько чисел в отрезке 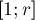 ? Их количество равно:
? Их количество равно:
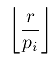
Однако если мы просто просуммируем эти числа, то получим неправильный ответ — некоторые числа будут просуммированы несколько раз (те, которые делятся сразу на несколько 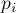 ). Поэтому надо воспользоваться формулой включений-исключений.
). Поэтому надо воспользоваться формулой включений-исключений.
Например, можно за 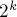 -ых, посчитать их произведение, и прибавить или вычесть в формуле включений-исключений очередное слагаемое.
-ых, посчитать их произведение, и прибавить или вычесть в формуле включений-исключений очередное слагаемое.
Итоговая реализация для подсчета количества взаимно простых чисел:
Асимптотика решения составляет 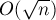 .
.
Даны 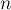 .
.
Алгоритм решения практически совпадает с предыдущей задачей — делаем формулу включений-исключений над числами 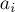 (иными словами, делящихся на их наименьшее общее кратное).
(иными словами, делящихся на их наименьшее общее кратное).
Таким образом, решение сводится к тому, чтобы за 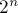 операций найти их наименьшее общее кратное, и прибавить или вычесть из ответа очередное значение.
операций найти их наименьшее общее кратное, и прибавить или вычесть из ответа очередное значение.
Дано 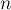 паттернам.
паттернам.
Заметим вначале, что мы можем легко посчитать число строк, удовлетворяющих сразу всем указанным паттернам. Для этого надо просто "пересечь" эти паттерны: посмотреть на первый символ (во всех ли паттернах на первой позиции стоит вопрос, или не во всех — тогда первый символ определен однозначно), на второй символ, и т.д.
Научимся теперь решать первый вариант задачи: когда искомые строки должны удовлетворять ровно 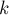 паттернам.
паттернам.
Для этого переберем и зафксируем конкретное подмножество 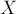 , и либо прибавляем к текущему ответу, либо отнимаем от него количество строк, подходящих под текущее множество:
, и либо прибавляем к текущему ответу, либо отнимаем от него количество строк, подходящих под текущее множество:
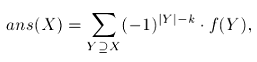
где 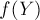 .
.
Если мы просуммируем 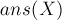 , то получим ответ:
, то получим ответ:
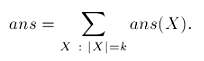
Однако тем самым мы получили решение за время порядка 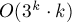 .
.
Решение можно ускорить, заметив, что в разных 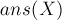 .
.
Перевернем формулу включений-исключений и будем вести суммирование по 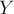 :
:
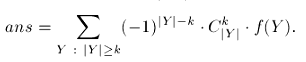
Решение получилось с асимптотикой 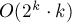 .
.
Перейдем теперь ко второму варианту задачи: когда искомые строки должны удовлетворять как минимум 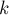 паттернам.
паттернам.
Понятно, мы можем просто воспользоваться решением первого варианта задачи и просуммировать ответы от 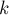 .
.
Таким образом, в итоговой формуле перед 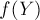 будет стоять другой коэффициент: не один биномиальный коэффициент с каким-то знаком, а их сумма:
будет стоять другой коэффициент: не один биномиальный коэффициент с каким-то знаком, а их сумма:
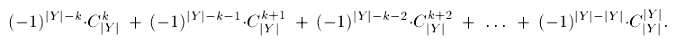
Заглянув в Грэхема (Грэхем, Кнут, Паташник. "Конкретная математика" [1998] ), мы видим такую известную формулу для биномиальных коэффициентов:
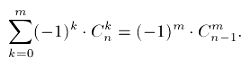
Применяя ее здесь, получаем, что вся эта сумма биномиальных коэффициентов сворачивается в:
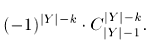
Таким образом, для этого варианта задачи мы также получили решение с асимптотикой 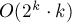 :
:

Есть поле 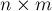 , избежав все препятствия. Требуется посчитать число путей, которыми он может это сделать.
, избежав все препятствия. Требуется посчитать число путей, которыми он может это сделать.
Предполагаем, что размеры 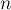 ).
).
Для решения сразу в целях удобства отсортируем препятствия в том порядке, в каком мы можем их обойти: т.е., например, по координате 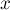 .
.
Также сразу научимся решать задачу без препятствий: т.е. научимся считать число способов дойти от одной клетки до другой. Если по одной координате нам надо пройти 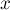 клеток, то из несложной комбинаторики мы получаем такую формулу через биномиальные коэффициенты:
клеток, то из несложной комбинаторики мы получаем такую формулу через биномиальные коэффициенты:
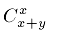
Теперь чтобы посчитать число способов дойти от одной клетки до другой, избежав всех препятствий, можно воспользоваться формулой включений-исключений: посчитаем число способов дойти, наступив хотя бы на одно препятствие.
Для этого можно, например, перебрать подмножество тех препятствий, на которые мы точно наступим, посчитать число способов сделать это (просто перемножив число способов дойти от стартовой клетки до первого из выбранных препятствий, от первого препятствия до второго, и так далее), и затем прибавить или отнять это число от ответа, в соответствии со стандартной формулой включений-исключений.
Однако это снова будет неполиномиальное решение — за асимптотику 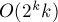 . Покажем, как получить полиномиальное решение.
. Покажем, как получить полиномиальное решение.
Решать будем динамическим программированием: научимся вычислять числа 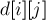 точки, поскольку к препятствиям добавляются стартовая и конечная клетки.
точки, поскольку к препятствиям добавляются стартовая и конечная клетки.
Если мы на секунду забудем про все препятствия и просто посчитаем число путей из клетки 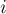
Таким образом, значение 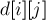 .
.
Дано 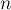 . Требуется посчитать количество способов выбрать из них четыре числа так, что их совокупный наибольший общий делитель равен единице.
. Требуется посчитать количество способов выбрать из них четыре числа так, что их совокупный наибольший общий делитель равен единице.
Будем решать обратную задачу — посчитаем число "плохих" четверок, т.е. таких четверок, в которых все числа делятся на число 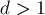 .
.
Воспользуемся формулой включений-исключений, суммируя количество четверок, делящихся на делитель 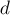 (но, возможно, делящихся и на больший делитель):
(но, возможно, делящихся и на больший делитель):
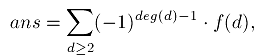
где 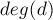 .
.
Чтобы посчитать функцию 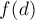 , и биномиальным коэффициентом посчитать число способов выбрать из них четверку.
, и биномиальным коэффициентом посчитать число способов выбрать из них четверку.
Таким образом, с помощью формулы включений-исключений мы суммируем количество четверок, делящихся на простые числа, затем отнимаем число четверок, делящихся на произведение двух простых, прибавляем четверки, делящиеся на три простых, и т.д.
Дано число  , что они являются гармоническими тройками, т.е.:
, что они являются гармоническими тройками, т.е.:
либо  ,
,
либо 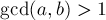 .
.
Во-первых, сразу перейдем к обратной задаче — т.е. посчитаем число негармонических троек.
Во-вторых, заметим, что в любой негармонической тройке ровно два ее числа находятся в такой ситуации, что это число взаимно просто с одним числом тройки и не взаимно просто с другим числом тройки.
Таким образом, количество негармонических троек равно сумме по всем числам от 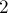 произведений количества взаимно простых с текущим числом чисел на количество не взаимно простых чисел.
произведений количества взаимно простых с текущим числом чисел на количество не взаимно простых чисел.
Теперь все, что нам осталось для решения задачи — это научиться считать для каждого числа в отрезке 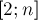 , и затем перебора всевозможных произведений простых чисел из факторизации.
, и затем перебора всевозможных произведений простых чисел из факторизации.
Поэтому нам понадобится более быстрое решение, которое подсчитывает ответы для всех чисел из отрезка 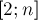 сразу.
сразу.
Для этого можно реализовать такую модификацию решета Эратосфена:
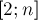 , в факторизации которых никакое простое не входит дважды. Кроме того, для формулы включений-исключений нам потребуется знать, сколько простых содержит факторизация каждого такого числа.
, в факторизации которых никакое простое не входит дважды. Кроме того, для формулы включений-исключений нам потребуется знать, сколько простых содержит факторизация каждого такого числа.
Для этого нам надо завести массивы 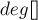 или нет.
или нет.
После этого во время решета Эратосфена при обработке очередного простого числа мы пройдемся по всем числам, кратным текущему числу, и увеличим 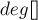 .
.
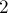 — количество чисел, не взаимно простых с данным.
— количество чисел, не взаимно простых с данным.
Для этого вспомним, как работает формула включений-исключений — здесь фактически мы реализуем ее же, но с перевернутой логикой: мы словно перебираем слагаемое и смотрим, в какие формулы включений-исключений для каких чисел это слагаемое входит.
Итак, пусть у нас есть число 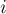 нечетна, то надо прибавлять, иначе вычитать.
нечетна, то надо прибавлять, иначе вычитать.
Реализация:

Асимптотика такого решения составляет 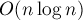 итераций вложенного цикла.
итераций вложенного цикла.
Докажем, что число перестановок длины 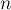 без неподвижных точек равно следующему числу:
без неподвижных точек равно следующему числу:
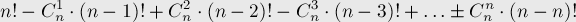
и приблизительно равно числу:
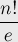
(более того, если округлить это выражение к ближайшему целому — то получится в точности число перестановок без неподвижных точек)
Обозначим через  ).
).
Воспользуемся теперь формулой включений-исключений, чтобы посчитать число перестановок хотя бы с одной неподвижной точкой. Для этого нам надо научиться считать размеры множеств-пересечений 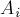 , они выглядят следующим образом:
, они выглядят следующим образом:
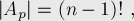
поскольку если мы знаем, что число неподвижных точек равно 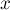 элементов могут стоять где угодно.
элементов могут стоять где угодно.
Подставляя это в формулу включений-исключений и учитывая, что число способов выбрать подмножество размера 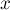 , получаем формулу для числа перестановок хотя бы с одной неподвижной точкой:
, получаем формулу для числа перестановок хотя бы с одной неподвижной точкой:
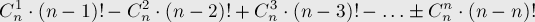
Тогда число перестановок без неподвижных точек равно:
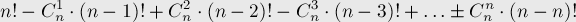
Упрощая это выражение, получаем точное и приблизительное выражения для количества перестановок без неподвижных точек:
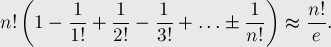
(поскольку сумма в скобках — это первые 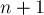 )
)
В заключение стоит отметить, что аналогичным образом решается задача, когда требуется, чтобы неподвижных точек не было среди m первых элементов перестановок (а не среди всех, как мы только что решали). Формула получится такая, как приведенная выше точная формула, только в ней сумма будет идти до k, а не до n.
Беспорядок (Derangement) — это перестановка чисел от 1 , в которой ни один элемент не стоит на своем месте.
Теорема:
Количество беспорядков порядка n
Доказательство:
Воспользуемся принципом включения-исключения: обозначим за 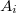 -ый элемент стоит на своем месте. Тогда по формуле включения-исключения имеем:
-ый элемент стоит на своем месте. Тогда по формуле включения-исключения имеем:
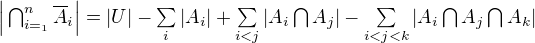 .
.
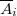 -ом месте.
-ом месте.
Таким образом 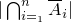 ,то есть количество искомых беспорядков.
,то есть количество искомых беспорядков.
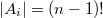
Рассмотрим 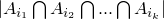 . Таким образом получаем, что:
. Таким образом получаем, что:
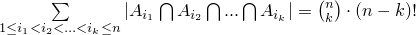
Подставляя соответствующие значения мощностей множеств в формулу включения-исключения, получаем:
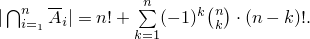
Раскрывая 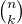 .
.
Задача 1. Из 100 школьников английский знают 42, немецкий — 30, французский — 28, английский и немецкий — 5, английский и французский — 10, немецкий и французский — 8, английский, немецкий и французский — 3 школьника. Сколько школьников не знают ни одного языка?
Решение. I способ.
Обозначим через А — множество школьников, знающих английский язык; N — множество школьников, знающих немецкий язык; F — множество школьников, знающих французский язык.
Тогда n(A) = 42, n(N) = 30, n(F) = 28, n(A ∩ N) = 5,
n(A ∩ F) = 10, n(N ∩ F) = 8, n(A ∩ N ∩ F) = 3.
Найдем с помощью формулы включений и исключений количество школьников, знающих хотя бы один из перечисленных иностранных языков.
n(A ∪ N ∪ F) = n(A) + n(N) + n(F) =
= n(A ∩ N) – n(A ∩ F) – n(N ∩ F) + n(A ∩ N ∩ F) =
= 42 + 30 + 28 – 5 – 10 – 8 + 3 = 80.
Следовательно, не знают ни одного иностранного языка:
100 – 80 = 20 школьников.
II способ.
Эту же задачу можно решить с помощью диаграммы Эйлера-Венна (рис. 1).

Так как 3 языка знают 3 школьника, то английский и немецкий знают 5 – 3 = 2, английский и французский — 10 – 3 = 7,
немецкий и французский — 8 – 3 = 5 школьников.
Только английский знают 42 –(2 + 3 + 7) = 30,
только немецкий — 30 – (2 + 3 + 5) = 20,
только французский — 28 – (3 + 5 + 7) = 13 школьников.
Ни одного языка не знают 100 – (2 + 3 + 5 + 7 + 13 + 20 + 30) = 20 школьников.
Задача 2. Сколько двузначных чисел не делятся ни на 2, ни на 3, ни на 5, ни на 11?
Решение. Обозначим: А — множество двузначных чисел, делящихся на 2;
В — множество двузначных чисел, делящихся на 3;
С — множество двузначных чисел, делящихся на 5;
D — множество двузначных чисел, делящихся на 11.
n(A ∪ B ∪ C ∪ D) — количество двузначных чисел, делящихся хотя бы на одно из чисел 2; 3; 5; 11.
n(A ∪ B ∪ C ∪ D) = n(A) + n(B) + n(C) + n(D) –
– n(A ∩ B) – n(A ∩ C) – n(A ∩ D) – n(B ∩ C) –
– n(B ∩ D) – n(C ∩ D) + n(A ∩ B ∩ C) + n(A ∩ B ∩ D) +
+ n(A ∩ C ∩ D) + n(B ∩ C ∩ D) – n(A ∩ B ∩ C ∩ D).
n(A) = 45, n(B) = 30, n(C) = 18, n(D) = 9,
n(A ∩ B) = 15, n(A ∩ C) = 9, n(A ∩ D) = 4, n(B ∩ C) = 6,
n(B ∩ D) = 3, n(C ∩ D) = 1, n(A ∩ B ∩ C) = 3,
n(A ∩ B ∩ D) = 1, n(A ∩ C ∩ D) = n(B ∩ C ∩ D) = n(A ∩ B ∩ C ∩ D) = 0.
Итак, n(A ∪ B ∪ C ∪ D) = 45 + 30 +18 + 9 – 15 – 9 – 4 – 6 – 3 – 1 + 3 + 1 = 68.
Так как всего 90 двузначных чисел, то чисел, не делящихся ни на одно из заданных чисел:
90 – 68 = 22.
Задача 3. Известно, что из n учеников спортом увлекаются a учеников, программированием b, математикой c, спортом и программированием d, спортом и математикой e, программированием и математикой f , спортом, математикой и программированием g учеников. Сколько учеников увлекается только программированием? Сколько учеников увлекается только математикой? Сколько учеников ничем не увлекается?
|
Вариант |
n |
a |
b |
c |
d |
e |
f |
g |
|
14 |
70 |
32 |
21 |
23 |
8 |
12 |
4 |
3 |
Решение. Пусть A —множество учеников, которые увлекаются спортом,
B — программированием, С - математикой.
Тогда |A| = 32, |B| = 21, |C| = 23, |A ∩ B| = 8, |A ∩ C| = 12, |B ∩ C| =4 |A ∩ B ∩ C| = 3
|(A ∩ B) ∪ ( B ∩ C) | = |A ∩ B| + |B ∩ C| − |A ∩ B ∩ C| = 8 + 4 – 3 = 9
На этом все! Теперь вы знаете все про формула включений-исключений, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое формула включений-исключений, принцип включений-исключений, беспорядок, derangement и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.