Лекция
Привет, Вы узнаете о том , что такое операции над множествами, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое операции над множествами, круги эйлера, двухместные операции над множествами, важность упорядоченности , настоятельно рекомендую прочитать все из категории Теория конечных автоматов.
Множества можно определять при помощи операций над некоторыми другими множествами и подмножествами. Пусть дана некоторая совокупность предметов, которую можно обозначить как множество
V ={ a, b, c, d, e, f, g, h, i, j, k }.
Предположим, что часть предметов, а именно: a, b, d и f имеют круглую форму, а часть – b, c, d, h, и i – окрашена в белый цвет. В этом случае говорят, что множество V имеет два подмножества А = { a, b, d, f } и В = { b, c, d, h, i } круглых и белых предметов. Можно говорить иначе: исходное множество называется фундаментальным или универсумом, а подмножества А и В – просто множествами.
В результате получим четыре класса элементов:
С0 ={ e, g, j, k } – элементы, которые не обладают ни одним из названных свойств,
С1 ={ a, f } – элементы, обладающие только свойством А (круглые),
С2 ={ c, h, i } – элементы, обладающие только свойством В (белые),
С3 ={ b, d } – элементы, обладающие одновременно двумя свойствами.
операции над множествами удобно изображать с помощью графической диаграммы Эйлера-Венна (рис. 1).
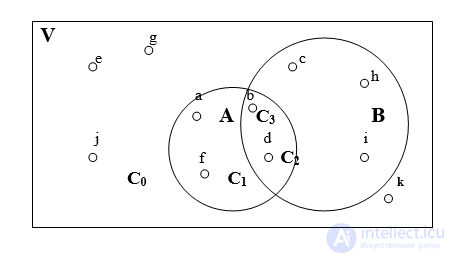
Рис. 1 . Диаграмма Эйлера-Венна для двух множеств А и В
Объединением множеств А = { a, b, d, f } и В = { b, c, d, h, i } назовем множество А ∪ В = { a, b, c, d, f, h, i }. Таким образом, объединением охватываются три класса элементов – С1, С2, С3, которые на диаграмме заштрихованы (рис. 2). При этом оба множества могут и не пересекаться, т.е. не иметь общих элементов. Логическую операцию объединения двух множеств можно охарактеризовать словами: элемент принадлежит множеству А или множеству В. То, что элемент х принадлежит А или В, можно выразить формулой
х ∈ А ∪ В = (х ∈ А) ∨ (х ∈ В),
где ∨ – символ логической связки или, которая называется дизъюнкцией.
Пересечением множеств А и В называется множество K = А ∩В, содержащее те элементы из А и В, которые входят одновременно в оба множества. Для нашего примера будем иметь (рис. 3):
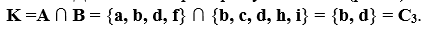
То, что элемент х принадлежит одновременно двум множествам А и В, можно выразить формулой

где ∧ – символ логической связки и, которая называется конъюнкцией.
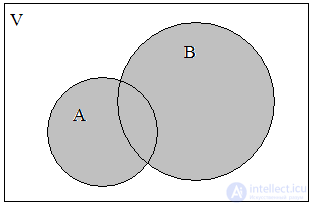
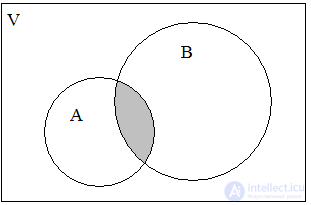
Рис. 2. А ∪ В Рис. 3. А ∩ В
Рассмотрим области С1 и С3, образующие множество А (рис. 4). Тогда области С2 и С0 образуют множество элементов, не входящих в А (рис. 5). Это обозначается как  . Об этом говорит сайт https://intellect.icu . Объединение или дизъюнкция множеств А и
. Об этом говорит сайт https://intellect.icu . Объединение или дизъюнкция множеств А и  даст весь универсум
даст весь универсум 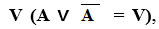 а пересечение или конъюнкция даст нам нулевое множество Ø; (
а пересечение или конъюнкция даст нам нулевое множество Ø; ( ∧ А = Ø). Таким образом множество
∧ А = Ø). Таким образом множество  дополняет множество А до универсума V, отсюда название – дополнительное множество или дополнение как операция. Операцию дополнения иначе еще называют инверсией.
дополняет множество А до универсума V, отсюда название – дополнительное множество или дополнение как операция. Операцию дополнения иначе еще называют инверсией.
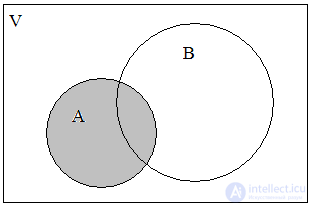
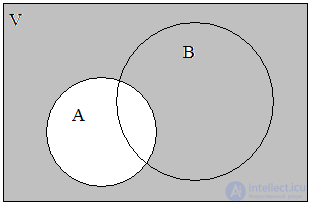
Рис. 4. А Рис. 5. 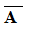
После рассмотрения операции инверсии (дополнения) все четыре области Сj на диаграмме можно выразить следующим образом:
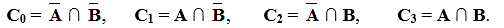
Используя инверсию, можно представить любую множественную операцию, например объединение:
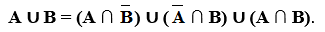
Операции дополнения или инверсии объединения и пересечения множеств называются соответственно стрелкой Пирса 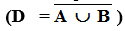 и штрихом Шеффера
и штрихом Шеффера 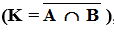 , которые обозначаются соответственно А↓В и А/В. Диаграммы для этих операций представлены на рис. 6 и 7.
, которые обозначаются соответственно А↓В и А/В. Диаграммы для этих операций представлены на рис. 6 и 7.
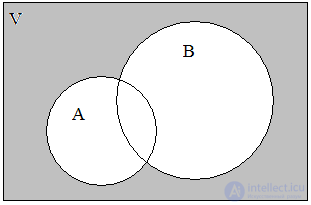
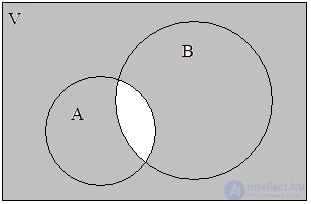
Рис. 6. А↓В Рис. 7. А/В
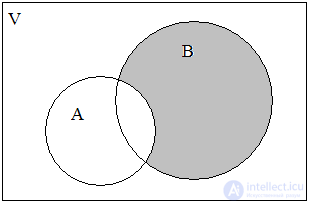
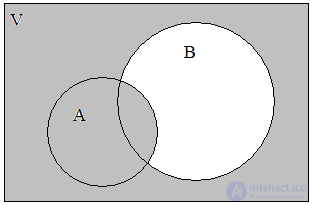
Рис. 8. ( В ← А ) Рис. 9. (В → А)
Разностью между множествами В и А называется совокупность тех элементов множества В, которые не вошли в множество А (рис. 8). Такая операция называется еще запретом А и обозначается ( В ← А ). Для нашего случая это будет область С2.
При этом 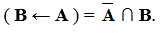
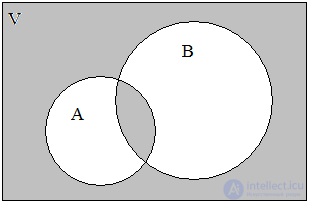
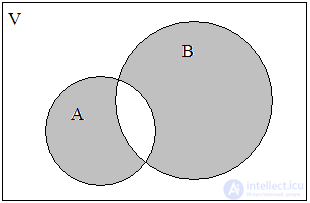
Рис. 10. (А ≡ В) Рис. 11. (А ⊕ В)
Дополнением к запрету служит импликация А. На диаграмме Эйлера-Венна это частичное включение множества В в множество А (рис. 9). Обозначается такая операция (В → А). При этом (В → А) = А ∪  .
.
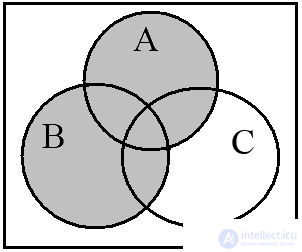
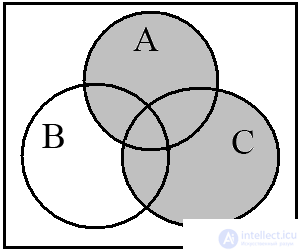
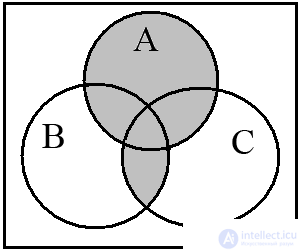
а b c
Рис. 12. (А ∪ В) ∩ (А ∪ С)
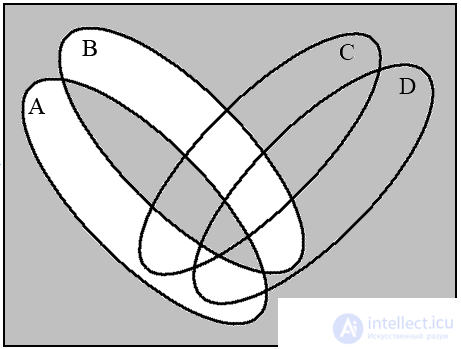
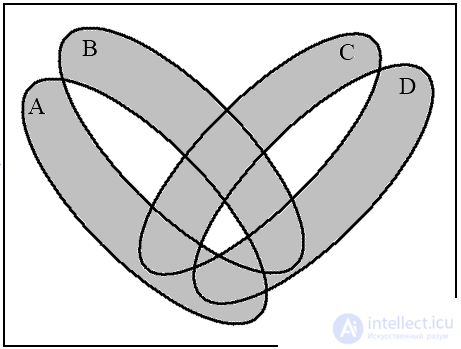
a (А ≡ B) b ((А≡ B)→(C ⊕ D))
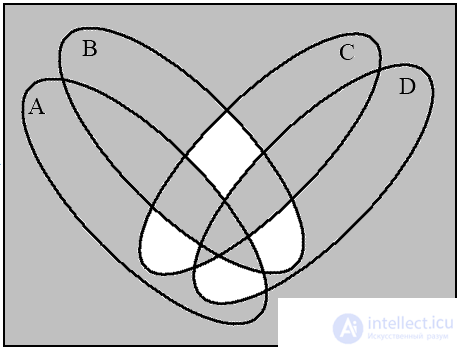
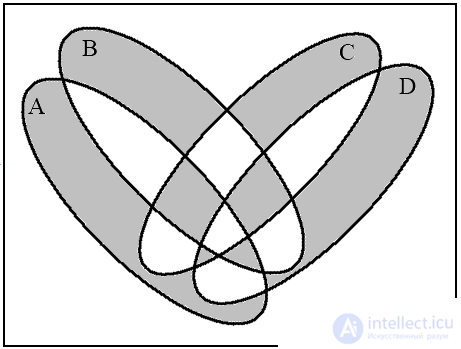
c 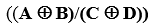 d
d 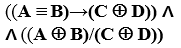
Рис.13. Диаграммы Венна для операций над четырьмя множествами
Аналогично определяются запрет В 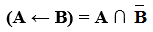
 и импликация В
и импликация В 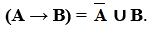
Остается привести еще две взаимно дополняющие операции – симметрическую разность или неравнозначность и эквивалентность или равнозначность.
Равнозначность определяется теми элементами множеств А и В, которые для них являются общими, а также элементами, не входящими ни в А, ни в В. В нашем случае это будут области С0 и С3 (рис. 10). Обозначается равнозначность А º В или А ~ В.
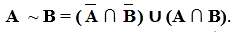
Неравнозначность есть объединение двух разностей или двух запретов. Эта операция обозначается (А В). Таким образом,
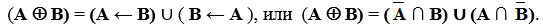
На диаграмме Эйлера-Венна это области С1 и С2 (рис. 11). Неравнозначность имеет еще название строгая дизъюнкция. Эту операцию можно передать словами: «либо А, либо В».
Диаграммы Эйлера-Венна достаточно наглядно иллюстрируют операции над тремя и четырьмя множествами. Рассмотрим операцию (А ∪ В) ∩ (А ∪ С) и построим диаграммы Эйлера-Венна для трех множеств. Диаграмма на рис. 12а изображает операцию (А ∪ В), а на рис. 12b – (А ∪ С). Конъюнкцию этих соотношений иллюстрирует результирующая диаграмма на рис. 12с.
Для четырех множеств четыре круга Эйлера не дают полную диаграмму Венна, поскольку их пересечение дает только 14 областей, а необходимо 16. Поэтому круги необходимо деформировать в эллипсы. Покажем на примере построение диаграммы для выражения 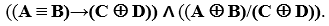
На рис. 13 изображены четыре диаграммы, соответствующие указанной последовательности операций. Последняя диаграмма (рис. 13d) является результирующей.
Двухместные операции - операции, в которых учувствуют два операнда. К двухместным операциям над множествами относятся:
Упорядоченное множество может представляться в виде списка или массива. Операции над упорядоченными множествами могут выполняться быстрее, так как имеют меньшую временную сложность. Например, приведенные двухместные операции выполняются на неупорядоченном множестве за O(n2), а на упорядоченном - за O(n).
Примеры:
пример реализации на Java определения пересечения неупорядоченного множества 
пример реализации на Java определения пересечения упорядоченного множества 
Анализ данных, представленных в статье про операции над множествами, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое операции над множествами, круги эйлера, двухместные операции над множествами, важность упорядоченности и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория конечных автоматов
Из статьи мы узнали кратко, но содержательно про операции над множествами
Комментарии
Оставить комментарий
Теория конечных автоматов
Термины: Теория конечных автоматов