Лекция
Привет, Вы узнаете о том , что такое булевы функции, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое булевы функции, таблица истинности, сднф , скнф, матрица карно, карты карно, карты карно , настоятельно рекомендую прочитать все из категории Теория конечных автоматов.
Булева функция ƒ(X1, Х2,...,Хn) - n-местная функция, аргументы и значения которой принадлежат множеству {0,1}.
Если логические высказывания могут принимать значения истинно или ложно, то для булевой функции аналогами этих значений будут значения 1 или 0. Для булевых функций справедливы таблицы истинности и основные равносильности алгебры высказываний.
Дополнительно вводятся операции:
Х1|Х2=Х1∧Х2 - штрих Шеффера и
X1↓X2=X1vX2- стрелка Пирса.
|
Х1 |
X2 |
¬X1 |
Х1∧Х2 |
X1vX2 |
X1⇒X2 |
Х1⇔Х2 |
X1| X2 |
Х1 ↓ X2 |
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
Дадим определения, необходимые для задания булевых функций.
Элементарная конъюнкция (дизъюнкция) – это логическое произведение (сумма) любого числа независимых логических переменных, входящих в нее с инверсией или без инверсии не более одного раза. Число входных переменных называется рангом элементарной конъюнкции (дизъюнкции).
Соседними называются элементарные конъюнкции (дизъюнкции) одного и того же ранга, содержащие одни и те же переменные, но отличающиеся знаком инверсии одной из переменных.
Дизъюнкция любого числа элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ), например:
(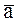 U b U
U b U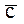 ) U (
) U (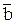 U c ) U
U c ) U 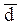 или
или 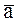 b
b 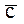 +
+ 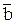 c +
c + 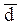
Конъюнкция любого числа элементарных дизъюнкций называется конъюнктивной нормальной формой (КНФ), например:
(a U b U 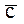 )U (
)U (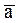 U
U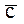 U d) U (
U d) U (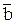 U
U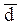 ) или (a + b +
) или (a + b + 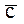 ) (
) (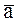 +
+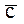 + d) (
+ d) ( 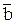 +
+ 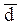 ) (далее для упрощения восприятия булевых функций будем использовать второй вид записи).
) (далее для упрощения восприятия булевых функций будем использовать второй вид записи).
Теоремы разложения (см. п.п. 2.2) можно применить ко всем переменным, определяющим булеву функцию, тогда, например, используя первую теорему разложения для функции трех переменных f(a,b,c), получим:
f(a,b,c) = a·b·c·f(1,1,1) + 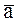 ·b·c· f (0,1,1) + a·
·b·c· f (0,1,1) + a·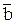 ·c·f(1,0,1) + a·b·
·c·f(1,0,1) + a·b·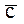 ·f(1,1,0) + +
·f(1,1,0) + +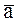 ·
·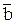 ·c·f(0,0 ,1) +
·c·f(0,0 ,1) + 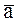 ·b·
·b·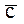 · f(0,1,0 ) + a·
· f(0,1,0 ) + a·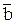 ·
·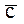 · f(1,0,0) +
· f(1,0,0) + 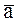 ·
·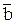 ·
·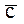 · f(0,0,0).
· f(0,0,0).
Каждая элементарная конъюнкция этого выражения составлена из набора всех переменных в прямом или инверсном виде и некоторого коэффициента, принимающего значение функции, если в ней положить равным единице прямое значение соответствующей переменной, а нулю – инверсное. Нетрудно заметить, что при этом по закону нулевого множества элементы с нулевым значением функции обратятся в ноль и останутся лишь наборы переменных при единичном значении функции, которые далее будем называть конституентами разложения единицы, или минтермами.
Если применить вторую теорему разложения, то получим форму разложения функции на конституенты нуля:
f(a,b,c) = [a+b+c+f(0,0,0) ] [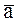 +b+c+f(1,0,0)] [a+
+b+c+f(1,0,0)] [a+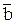 +c+f(0,1,0] [a+b+
+c+f(0,1,0] [a+b+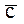 + +f(0,0,1)] U [
+ +f(0,0,1)] U [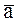 +
+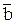 +c+f(1,1,0)] [
+c+f(1,1,0)] [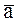 +b+
+b+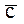 +f(1,0,1)] [a+
+f(1,0,1)] [a+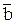 +
+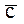 +f(0,1,1)] [
+f(0,1,1)] [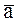 +
+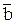 + +
+ +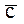 + f(1,1,1)].
+ f(1,1,1)].
Здесь, по закону универсального множества, каждая элементарная дизъюнкция с единичным значением функции принимает также единичное значение, и в результате остаются только те дизъюнкции переменных, инверсные значения которых определяют нулевое значение функции. Эти дизъюнкции называются конституентами разложения нуля, или макстермами. Такие методы разложения распространяются на функции с любым числом переменных.
Раскладывая булевы функции на конституенты, мы получаем т.н. совершенные формы. Совершенной дизъюнктивной формой ( сднф ) называется дизъюнкция конституентов единицы (минтермов), а совершенной конъюнктивной формой – конъюнкция конституентов нуля (макстермов).
Любую сколь угодно сложную булеву функцию можно преобразовать в ДНФ или КНФ, а затем в совершенные формы (СДНФ или скнф ). Для этого необходимо прежде всего, используя теорему де Моргáнa, исключить инверсии над функциями, перейдя к формам, в которых имеются инверсии только над одиночными переменными. Затем с использованием законов булевой алгебры привести логические выражения к дизъюнктивной или конъюнктивной формам. Понятие совершенных форм используется при минимизации функций и для определения равносильности. Две булевы функции считаются равносильными, если их СДНФ и СКНФ полностью совпадают.
Таблица 2.1 Одной из самых распространенных форм представления булевых функций является таблица истинности (таблица состояний).
|
Переменные |
Функция |
Десятичный эквивалент |
|||
|
a |
b |
c |
d |
Y |
|
|
0 |
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
1 |
1 |
1 |
|
0 |
0 |
1 |
0 |
0 |
2 |
|
0 |
0 |
1 |
1 |
1 |
3 |
|
0 |
1 |
0 |
1 |
1 |
5 |
|
0 |
1 |
1 |
1 |
0 |
7 |
|
1 |
0 |
0 |
0 |
1 |
8 |
|
1 |
0 |
0 |
1 |
0 |
9 |
|
1 |
1 |
0 |
1 |
0 |
13 |
|
1 |
1 |
1 |
1 |
0 |
15 |
Таблица истинности определяет значение функции для всех возможных состояний входных переменных. Поскольку любая логическая переменная может принимать только два значения – 0 и 1, то для булевой функции «n» входных переменных число значений будет определяться показательной функцией 2n.
Функция является полностью определенной, если для любого набора входных переменных известны ее значения (0 или 1).
Булева функция является не полностью определенной (неполной), если есть один или несколько наборов переменных, при которых значение функции не определено (может быть и 0, и 1) или ее не существует. Такие значения функции называются фиктивными(Ф). Пример задания не полностью определенной функции представлен табл. 2.1.
Каждый набор логических переменных представлен двоичным числом n-го разряда, и ему, следовательно, соответствует определенное десятичное число. Десятичное число, соответствующее двоичному набору логических переменных, называется десятичным эквивалентом. Таким образом, булеву функцию можно представить с помощью десятичных эквивалентов:
Y1 = { 0,1,3,5,8} ; Y0 = {2,7,9,13,15}.
Оставшиеся наборы, не заданные таблицей истинности, по всей вероятности, будут фиктивными YФ = {4,6,10,11,12,14}.
По таблице истинности можно получить совершенные формы записи булевых функций. Так, для записи в виде СДНФ нужно из таблицы выбрать единичные наборы переменных, представить их в виде конституентов единицы и произвести их дизъюнкцию.
СДНФ: 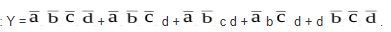
Для записи в форме СКНФ нужно выбрать из таблицы нулевые наборы переменных, проинвертировать переменные в каждом из этих наборов, представить в виде конституентов нуля и произвести их конъюнкцию.
СКНФ: 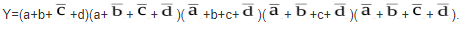
Аналогично можно составить СДНФ и СКНФ по десятичным эквивалентам, определяющим булеву функцию.
СДНФ (совершенная дизъюнктивная нормальная форма)
СКНФ (совершенная конъюнктивная нормальная форма)
Каждая логическая функция имеет одну СДНФ и одну СКНФ.
СДНФ логической функции – это дизъюнкция конституент единицы (минтермов), соответствующих наборам входных переменных, для которых функция равна 1.
В общем случае СДНФ можно представить в форме:
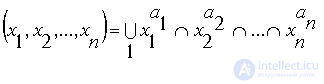
где а1, а2, … , аn – двоичный набор,

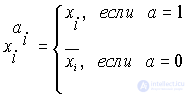
СКНФ логической функции – это конъюнкция конституент нуля (макстермов), соответствующих входным наборам, для которых функция равна 0.
В общем случае СКНФ можно представить в форме:
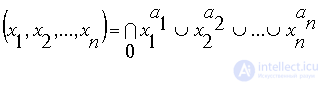
Конституента единицы (нуля) – это элементарная конъюнкция (дизъюнкция), в которую входят все n переменных в прямом или инверсном виде.
Форма представления логической функции, описывающей работу элемента, выбирается из соображений минимизации членов уравнения. СДНФ выбирается в случае, если в таблице истинности для логической функции преобладает число состояний логического нуля, СКНФ – логической единицы
Алгоритм перехода от таблицы истинности логической функции к ее записи в виде СДНФ:
Алгоритм перехода от таблицы истинности логической функции к ее записи в виде СКНФ:
|
Совершенные формы |
Формула |
|
Совершенная конъюнктивная нормальная форма(СКНФ)— конъюнкция конституент нуля |
|
|
Совершенная дизъюнктивная нормальная форма(СДНФ) -дизъюнкция конституент единицы |
где а1, а2, … , аn – двоичный набор,
|
ПРИМЕР :
| Таблица 2.1 | ||
| х1х2х3 | F1 | F2 |
| 000 | 0 | 0 |
| 001 | 1 | 0 |
| 010 | 1 | 0 |
| 011 | 0 | 1 |
| 100 | 0 | 0 |
| 101 | 0 | 1 |
| 110 | 0 | 1 |
| 111 | 1 | 1 |
F1=/x1/x2x3 v /x1x2/x3 v x1x2x3
F2=/x1x2x3 v x1/x2x3 v x1x2/x3 v x1x2x3
Другая известная форма носит название совершенной конъюнктивной нормальной формы (СКНФ). Она строится аналогично СДНФ.
Конституента 0 - функция f(x1, x2, ... xn) принимающая значение 0 только на единственном наборе.
Конституента нуля записывается в виде элементарной дизъюнкции всех переменных. Каждому набору соответствует своя конституента 0. Например, набору 0110 переменных х1х2х3х4соответствует конституента нуля х1 v /х2 v /х3 v х4. СКНФ представляется как конъюнкция конституент нуля, соответствующих нулевым наборам функции."
ПРИМЕР. Для рассмотренных функций в табл. 2.1 построим СКНФ:
F1=(x1 v x2 v x3) (x1 v /x2 v /x3) (/x1 v x2 v x3) (/x1 v x2 v /x3) (/x1 v /x2 v x3)
F2=(x1 v x2 v x3) (x1 v x2 v /x3) (x1 v /x2 v x3) (/x1 v x2 v x3)
Матрица Карно представляет собой специально организованные таблицы соответствия, обладающие тем замечательным свойством, что любые две соседние клетки матрицы определяют «соседние» наборы переменных, т.е. Об этом говорит сайт https://intellect.icu . наборы, отличающиеся значением только одной переменной. Клетки, расположенные по краям матрицы, также являются соседними и обладают этим свойством. Это достигается благодаря кодированию столбцов и строк матрицы специальным циклическим кодом Грея.
Еще одним свойством матриц Карно является то, что при увеличении количества переменных на единицу матрица увеличивается вдвое, поскольку число клеток матрицы определяется показательной функцией «2n».
В клетках матрицы, как в таблице истинности, проставляются значения определяемой булевой функции – 0 или 1. Клетки, соответствующие фиктивным состояниям, обычно оставляют пустыми. Например, на рис. 2.1а представлена матрица Карно, определяющая функцию, заданную таблицей истинности (табл. 2.1). По сути дела, матрица Карно – это та же таблица состояний, но в более компактной форме.
На рис. 2.1b, c, d показаны соответственно матрицы Карно для двух, трех и пяти переменных.
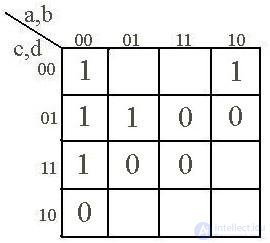
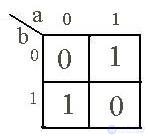
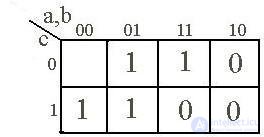
a b c
d
Рис. 2.1.
Является одним из эквивалентных способов описания или задания логический функций наряду с таблицей истинности или выражениями булевой алгебры. Преобразование карты карно в таблицу истинности или в булеву формулу и обратно осуществляется элементарным алгоритмом.
Удобство и наглядность такого представления логической функции обусловлено тем, что логические термы, к которым могут быть применены операции попарного неполного склеивания и элементарного поглощения группируются в карте Карно в виде визуально очевидных прямоугольных массивов, содержащих в своих ячейках одинаковые значения (нули и единицы).
Карты Карно можно рассматривать как развертку на плоскость n-мерного булева куба, причем размерность этого гиперкуба совпадает с количеством переменных представляемой функции, а каждая вершина гиперкуба взаимно однозначно соответствует одной клетке карты Карно. Графически карта Карно изображается в виде прямоугольника или квадрата из ячеек, число которых равно {\displaystyle 2^{n}}, причем любые две соседние ячейки по вертикали или горизонтали или, иными словами — в окрестности фон Неймана описывают термы, различающиеся только по одной переменной — с логическим отрицанием и без логического отрицания. Также соседним являются первая и последняя строки, крайний левый и крайний правый столбцы таблицы, поэтому таблица Карно является фактически разверткой логического гиперкуба на поверхность тороида. Возможно построение самых различных карт для одной и той же функции, удовлетворяющих условию: геометрическое соседство ячеек в смысле фон Неймана — логическое соседство термов — то есть с расстоянием Хэмминга между термами соседних ячеек равным 1. Любая из таких таблиц одинаково удобна для минимизации функции, но обычно переменные по строкам и столбцам в карте Карно упорядочивают по рефлексивному коду Грея из-за мнемоничности и наглядности.
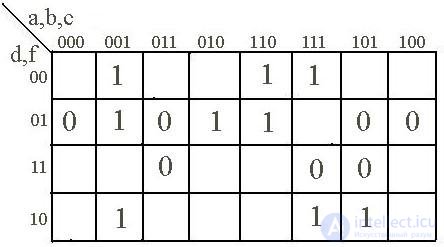
Пример карты Карно
Карты Карно были предложены в 1952 году Эдвардом В. Вейчем и усовершенствованы в 1953 году физиком из «Bell Labs» Морисом Карно (Maurice Karnaugh), чтобы упростить проектирование цифровых систем .
Карта Карно представляет собой таблицу истинности, отформатированную особым образом, пригодным для наглядной ручной минимизации. Результатом минимизации является либо дизъюнктивная нормальная форма (ДНФ), либо конъюнктивная нормальная форма (КНФ). В первом случае работа ведется с клетками карты, где находятся единицы, во втором — с клетками, где находятся нули. В исходной карте, как и в таблице истинности, каждая единица соответствует одному терму cовершенной дизъюнктивной нормальной форме (СДНФ), а каждый ноль — одному терму cовершенной конъюнктивной нормальной форме (СКНФ).
Рядом расположенные группы единиц или нулей на карте Карно объединяют в прямоугольные области или «склейки» размером клеток. Каждая такая группа в итоговой логической формуле будет соответствовать одному терму (если считать, что операция логического «ИЛИ» — это «суммирование», а операция логического «И» — это «перемножение», то один терм соответствует одному слагаемому в случае ДНФ, или одному сомножителю в случае КНФ), содержащему {\displaystyle n-a-b}
переменных, это группирование обычно называют «склейкой» . Таким образом, работа с картой сводится к выделению оптимального набора нескольких групп единиц (нулей) и преобразование их в логическое выражение.
Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами, содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть поглощению. Например:
Аналогично для КНФ:
Возможность поглощения следует из очевидных равенств:
Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для функций многих логических переменных может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких термов.
Булевы функции N переменных, представленные в виде СДНФ или СКНФ, могут иметь в своем составе не более чем различных термов. Все эти элементарные термы можно представить в виде некоторой структуры, топологически эквивалентной
-мерному кубу, причем любые два терма, соединенные ребром, пригодны для склейки и поглощения.
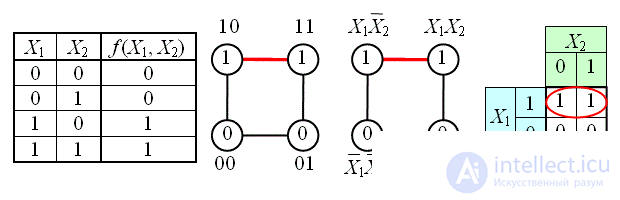
На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:
В случае функции трех переменных приходится иметь дело с трехмерным кубом. Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трех переменных и соответствующий ей куб.
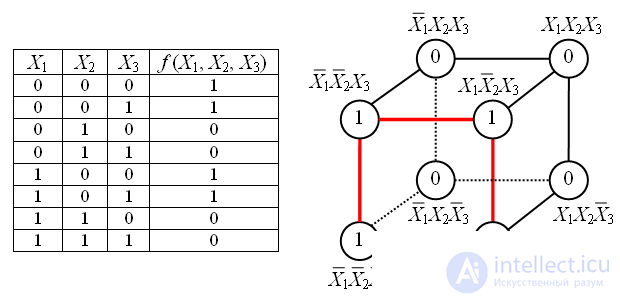
Как видно из рисунка, для трехмерного случая возможны более сложные конфигурации термов. Например, четыре терма, принадлежащие одной грани куба, объединяются в один терм с поглощением двух переменных:
В общем случае можно сказать, что {\displaystyle 2^{k}} термов, принадлежащие одной что {\displaystyle k}
-мерной грани гиперкуба, склеиваются в один терм, при этом поглощаются {\displaystyle k}
переменных.
Для упрощения работы с булевыми функциями большого числа переменных был предложен следующий удобный прием. Куб, представляющий собой структуру термов, разворачивается на плоскость, как показано на рисунке. Таким образом появляется возможность представлять булевы функции с числом переменных больше двух в виде плоской таблицы. При этом следует помнить, что порядок кодов термов в таблице (00 01 11 10) не соответствует порядку следования двоичных чисел записанных в лексикографическом порядке (00 01 10 11), а клетки, находящиеся в крайних столбцах таблицы, соседствуют между собой.
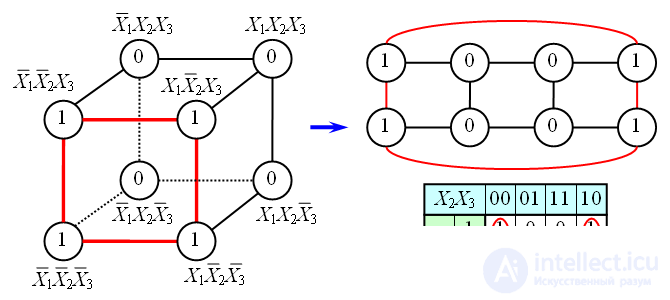
Аналогичным образом можно работать с логическими функциями большего числа переменных.
Традиционно существует несколько стилей представления карт Карно. Часто в шапке и левой колонке проставляются численные значения переменных, подобно тому, как они указаны в таблице истинности (а). В этом стиле наиболее очевидно, что карта Карно является своеобразной формой представления таблицы истинности. Однако клетки карты Карно следуют в несколько ином порядке, чем строки в таблице истинности, так как в таблице истинности принято строки упорядочивать в лексикографическом нарастании двоичных чисел. Например, в карте Карно для четырех переменных порядок следования ячеек карты и строк таблицы истинности совпадет, если переставить местами третий-четвертый столбцы и третью-четвертую строки карты.
Каждая строка таблицы истинности и каждая клетка карты Карно соответствует одному слагаемому ДНФ, поэтому в шапке и левой колонке карты можно указывать вхождения переменных (прямые и инверсные), как они выглядят в СДНФ (б). Существует сокращенный вариант этого стиля представления, где во вспомогательных строках и колонках указывается, в каком виде, прямом или инверсном, представлена каждая переменная в соответствующей строке или столбце карты (в).
Наконец, в некоторых случаях на краях карты линиями указываются столбцы и строки, где соответствующая переменная представлена в прямом виде (г).
а) 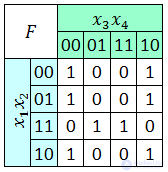 б)
б) 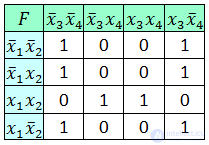 в)
в) 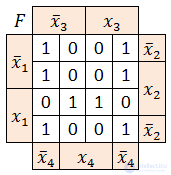 г)
г) 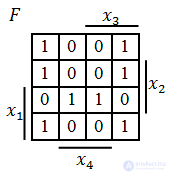
Исходной информацией для работы с картой Карно является таблица истинности минимизируемой функции. Таблица истинности содержит полную информацию о логической функции, задавая ее значения на всех возможных 2n наборах входных переменных X1 … Xn. Карта Карно также содержит 2n клеток, каждая из которых ассоциируется с уникальным набором входных переменных X1 … Xn. Таким образом, между таблицей истинности и картой Карно имеется взаимно однозначное соответствие, и карту Карно можно считать соответствующим образом отформатированной таблицей истинности.
В данном разделе в качестве примера используется функция четырех переменных, заданная таблицей истинности, изображенной на рис. 2а. Карта Карно для той же функции изображена на рис. 2б.
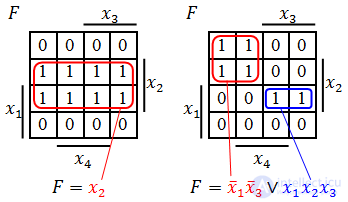
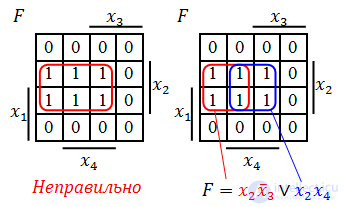
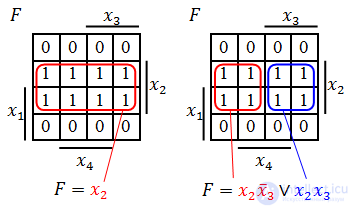
Прямоугольную область в карте Карно, которая состоит из 2k одинаковых значений (единиц или нулей в зависимости от того, какую форму нужно получить) будем называть склейкой, группой или областью. Распределение всех имеющихся в карте Карно нулей (единиц) по склейкам будем называть покрытием. С целью минимизации булевой функции необходимо построить такое покрытие карты Карно, чтобы количество склеек было минимальным, а размер каждой склейки максимально возможным. Для этого необходимо руководствоваться следующими правилами.
a) 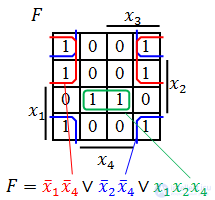 б)
б) 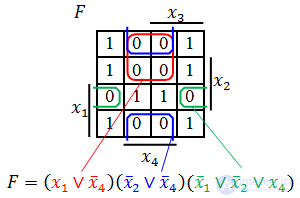
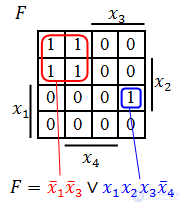


На практике встречаются случаи, когда при некоторых значениях аргументов булева функция не определена. Например, булева функция описывает цифровое устройство, у которого некоторые сочетания входных сигналов физически невозможны или же при некоторых значениях входных сигналов реакция устройства не имеет значения. В таких случаях говорят о «неопределенных условиях», а функция такого вида называется «частично определенной» или просто «частичной» .
На рисунке показано цифровое устройство F с четырьмя двоичными входными сигналами . Входными сигналами могут быть показания датчиков, работающих на замыкание и следовательно имеющих только два значения — «включено» (1) и «выключено» (0). Предположим, что в силу особенностей конструкции устройства 2-й и 4-й датчики не могут сработать одновременно, то есть сочетание сигналов
физически невозможно. В этом случае значение функции в четырех клетках карты Карно не имеет значения, что условно показано символом «×».
Такие клетки могут произвольным образом включаться в любые склейки, а также могут не включаться ни в какие склейки, то есть их по желанию можно доопределять и как 1, и как 0 .
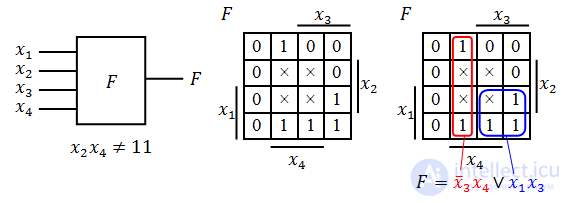
Карта Карно может быть построена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути Карта Карно — это таблица истинности, представленная в виде матрицы в 2-мерном виде.
Каждая клетка этой карты соответствует одной строке в классической таблице истинности и обозначается строкой переменных с инверсиями и без инверсий. Например, пусть в таблице истинности для функции 4 переменных одна из строк имеет вид: 0 1 1 0 | 1, тогда клетка в карте Карно, соответствующая этой строке, будет иметь имя
и в этой клетке ставится 1. Указание имен клеток в карте Карно обычно выполняется дополнительной строкой сверху и дополнительным столбцом слева.
Существенно, что в карте Карно соседние клетки обязательно имеют соседние, в смысле расстояния Хэмминга коды, то есть расстояние Хэмминга между соседними клетками равно 1, и различаются только состоянием — с инверсией или без, одной и только одной из переменных. Соседними клетками считаются клетки, примыкающие друг к другу стороной, также соседними клетками считаются клетки крайнего левого и крайнего правого столбцов и клетки первой и последней строк. Таком образом, карта Карно на плоскости топологически эквивалентна поверхности тора в трехмерном пространстве, или гипертору в пространстве с размерностью на 1 больше размерности соответствующей многомерной карты Карно.
Так как перестановка переменных в логической функции не изменяет саму функцию, то есть, например, или, что то же самое, — перестановка столбцов переменных в таблице истинности не изменяет функцию, существует несколько вариантов отображения таблицы истинности на карту Карно с сохранением «соседства» клеток. Но практически наиболее часто карту Карно заполняют, используя нарастающий код Грея для обозначения строк и столбцов. Такой подход гарантирует порождение карты Карно с избеганием субъективных ошибок.
При заполнении карты на пересечении строки и столбца проставляется соответствующее значение из таблицы истинности — 0 или 1. После того как карта заполнена, приступают к минимизации.
Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки, которые содержат единицы, если нужна КНФ, то рассматриваем те клетки, которые содержат нули. Сама минимизация производится по следующим правилам (на примере ДНФ).
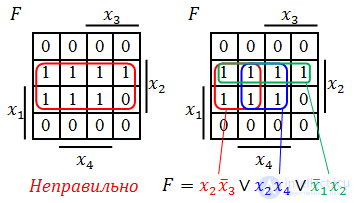
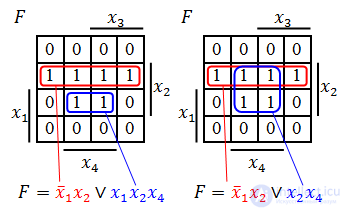
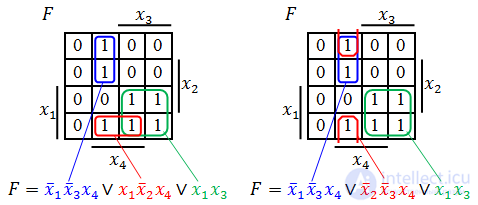
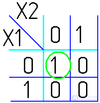
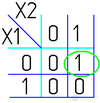
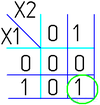
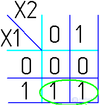
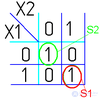
Далее берем первую область и смотрим, какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных; если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берем следующую область, выполняем то же самое, что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.
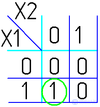
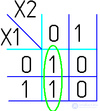
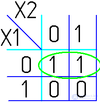
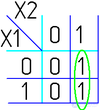
Например (для Карт на 2 переменные):
 |
 |
 |
 |
 |
 |
 |
 |
|||||||
| |
|
|
|
|
|
|
|
|||||||
 |
 |
 |
 |
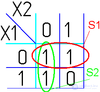 |
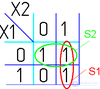 |
|||||||||
| |
|
|
|
|
|
|||||||||
| |
|
|
|
|
|
|||||||||
| |
|
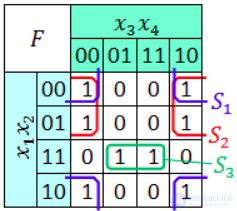
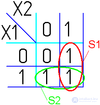
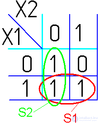
Для КНФ все то же самое, только рассматриваем клетки с нулями, неменяющиеся переменные в пределах одной области объединяем в дизъюнкции (инверсии проставляем над единичными переменными), а дизъюнкции областей объединяем в конъюнкцию. На этом минимизация считается законченной. Так, для Карты Карно на рис. 1, выражение в формате ДНФ будет иметь вид:
В формате КНФ:
Так же из ДНФ в КНФ и обратно можно перейти, использовав Законы де Моргана.
У мальчика Коли есть мама, папа, дедушка и бабушка. Коля пойдет гулять на улицу, тогда и только тогда, когда ему разрешат хотя бы двое родственников.
Для краткости обозначим родственников Коли через буквы:
мама — X1
папа — X2
дедушка — X3
бабушка — X4
Условимся обозначать согласие родственников единицей, несогласие — нулем. Возможность пойти погулять обозначим буквой f, Коля идет гулять — f = 1, Коля гулять не идет — f = 0.
Составим таблицу истинности:

Перерисуем таблицу истинности в 2-мерный вид:
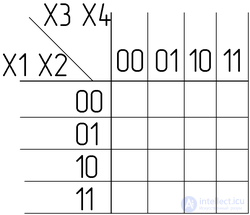
Переставим в ней строки и столбцы в соответствии с кодом Грея (последний и предпоследний столбец меняют местами). Получили Карту Карно:
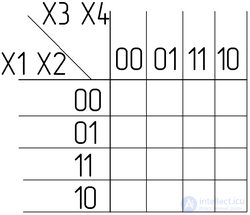
Заполним ее значениями из таблицы истинности (первая строка не соответствует таблице истинности, так как f=0 и разрешения на гулять нет):
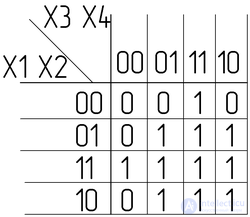
Минимизируем в соответствии с правилами:
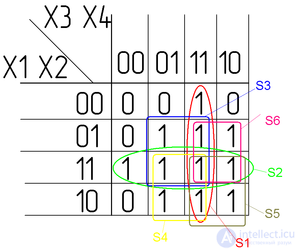
Теперь по полученной минимальной ДНФ можно построить логическую схему:
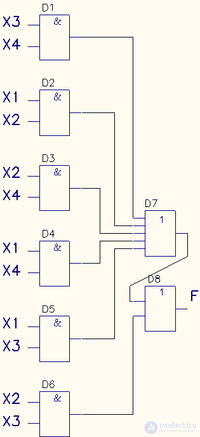
Из-за отсутствия в наличии шестивходового элемента ИЛИ, реализующего функцию дизъюнкции, пришлось каскадировать пяти- и двух-входовые элементы (D7, D8).
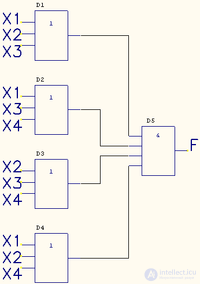
Составим мин. КНФ:

Анализ данных, представленных в статье про булевы функции, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое булевы функции, таблица истинности, сднф , скнф, матрица карно, карты карно, карты карно и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория конечных автоматов
Комментарии
Оставить комментарий
Теория конечных автоматов
Термины: Теория конечных автоматов