4.5 Деревья как связанный граф

Привет, Вы узнаете о том , что такое деревья как связанный граф, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое деревья как связанный граф, теория графов, деревья , настоятельно рекомендую прочитать все из категории Теория конечных автоматов.

В особый тип графов выделяются деревья . Дерево – это связанный граф , не имеющий циклов, так как любые две его вершины соединены простым путем. На рис. 4.14 показаны все пять видов деревьев, которые могут быть получены на шести вершинах.

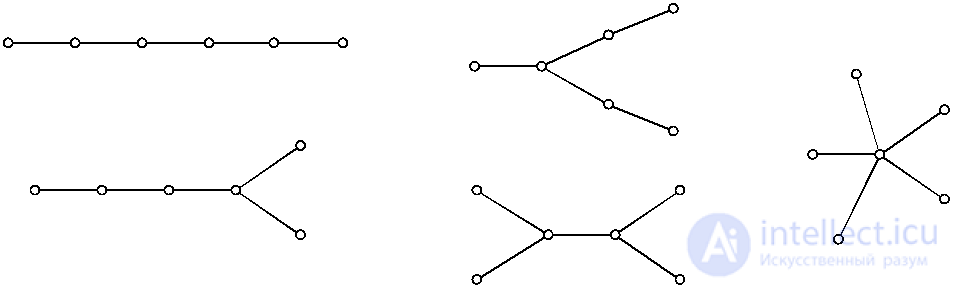
Рис. 4.14

Ориентированным деревом называется бесконтурный орграф, у которого отрицательная полустепень ρ– любой вершины не более 1 и существует ровно одна вершина, называемая корнем ориентированного дерева, у которой отрицательная степень ρ– = 0.

Опираясь на данное определение, можно доказать, что в ориентированном дереве любая вершина достижима из корня. Основные свойства деревьев описывает следующая теорема.

Теорема 4.3

1. В неориентированном дереве существуют по крайней мере две концевые вершины.

2. Между любыми двумя вершинами дерева имеется ровно один путь.

3. Число ребер в дереве всегда на единицу меньше числа вершин (m = n–1).

Поскольку в дереве все пути – простые, то в нем есть по крайней мере один максимальный путь, т. е. путь, который нельзя продолжить. Концы этого пути и являются концевыми вершинами.

Наличие пути между любой парой вершин следует из связности дерева, а единственность этого пути – из того, что существование двух путей между парой вершин всегда создает цикл.

Третий пункт теоремы проще всего доказать, используя понятие ориентированного дерева. Выберем в дереве произвольную вершину. Назовем ее корнем. Ребра, инцидентные корню, ориентируем в направлении от корня. Для каждой вершины vi, являющейся концом одного из этих ребер, ориентируем остальные инцидентные ей ребра в направлении от vi. Продолжаем эту процедуру до тех пор, пока не будут достигнуты концевые вершины. В силу единственности пути между вершинами ни одна вершина не будет достигнута дважды (т. е. не придется ориентировать уже ориентированные ребра), а в силу связности дерева все вершины будут достигнуты. Из этой процедуры видно, что корень не имеет входящих ребер, а все остальные вершины имеют по одному входящему ребру. Поскольку все ребра являются входящими для какой-то вершины и в процессе ориентации число вершин и ребер не изменилось, то отсюда и следует п. 3 теоремы.

Для ориентированных деревьев свойства 1 и 3 верны всегда, а свойство 2 – нет. Вот почему ориентированное дерево: 1) всегда слабо связно; 2) односторонне связно, только если оно является ориентированной цепью (т.е. когда все вершины лежат на единственном пути из корня); 3) никогда не бывает сильносвязным, поскольку сильно связный граф обязательно содержит цикл.

Для всех вершин ориентированного дерева, за исключением корня, отрицательная полустепень ρ– = 1, а положительная полустепень ρ+ может принимать любое значение от нуля. При этом те вершины, у которых положительная полустепень ρ+ = 0, называются листьями дерева. Ориентированное дерево, у которого каждая вершина, отличная от корня, есть лист, называется кустом.

Рассмотрим некоторые параметры, которые характеризуют ориентированное дерево.

v0 Уровень 3

v1 v2 v3 Уровень 2

v4 v5 v6 v7 v8 Уровень 1

v9 Уровень 0

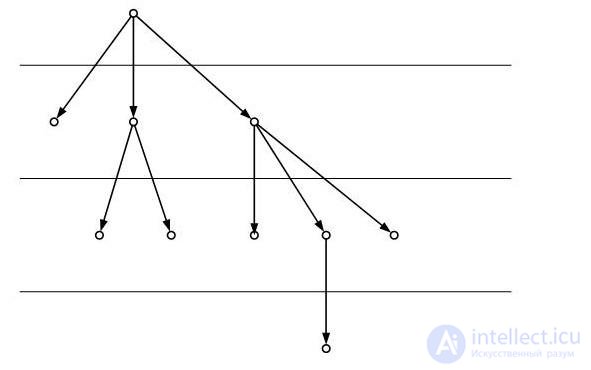
Рис. 4.15

Высота ориентированного дерева – это наибольшая длина пути из корня в лист; глубина вершины ориентированного дерева – это длина пути из корня в эту вершину; высота вершины – это наибольшая длина пути из данной вершины в лист и , наконец, уровень вершины ориентированного дерева – это разность между высотой ориентированного дерева и глубиной данной вершины. Об этом говорит сайт https://intellect.icu . Из этих определений можно сделать вывод, что уровень корня равен высоте дерева, но уровни различных листьев так же, как и их глубины, могут быть различны, однако высота любого листа равна нулю (рис. 4.15).

При идентификации деревьев удобной является корневая форма представления дерева. При выборе корня из дерева последовательно удаляются все концевые вершины и ребра до тех пор, пока не останется одна вершина или две. В первом случае оставшаяся вершина выбирается в качестве корня и называется центром. Во втором случае вершины и связывающее их ребро образуют бицентр.

При другом способе выбора корня дерева используется понятие высоты вершины. С каждой вершиной связаны ответвления, представляющие собой части дерева. В качестве корня выбирается вершина с наименьшей высотой и называется центроидом. Если имеются две такие вершины, то они вместе с объединяющим их ребром образуют бицентроид. При этом за корень принимается та вершина, из которой вырастает дерево с меньшим числом вершин.

Любую булеву функцию можно наглядно изобразить в виде ориентированного дерева. При этом листья этого дерева помечаются переменными или константами логического уравнения, а каждый узел, не являющийся листом, – одной из операций булевой алгебры. Пример такого дерева для функции

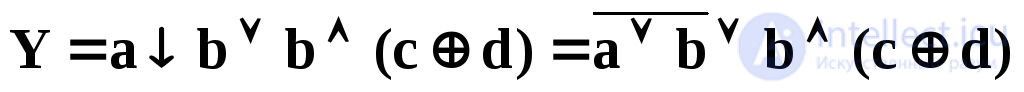
показан на рис. 4.16

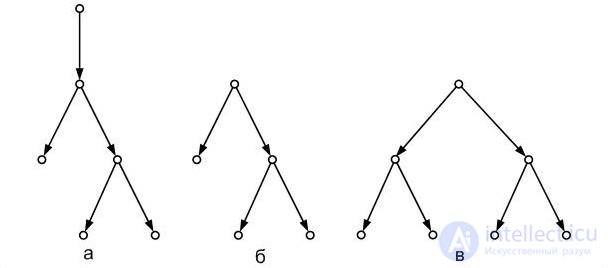
О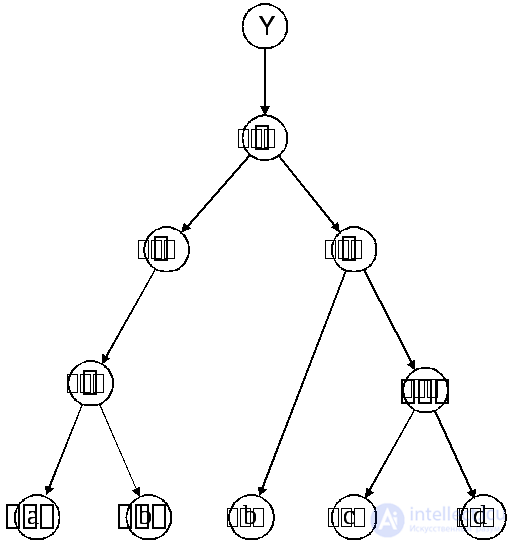риентированное дерево называютбинарным, если положительная полустепень любой его вершины не больше 2; бинарное ориентированное дерево называют полным, если из любой его вершины, не являющейся листом, исходят ровно две дуги, а уровни листьев совпадают. Примеры различных бинарных ориентированных деревьев приведены на рис. 4.17. На рис. 4.17а, б показаны неполные ориентированные бинарные деревья, на рис. 4.17в – полное. Рис. 4.16

Теорема 4.4 (теорема о высоте бинарного ориентированного дерева с заданным числом листьев). Бинарное ориентированное дерево с n листьями имеет высоту, не меньшую log2 n.

Эта теорема имеет одно весьма интересное приложение. Предположим, что необходимо расположить строго по возрастанию элементы конечного линейно упорядоченного множества {a1, ...,an}. Эту задачу называют задачей сортировки, а любой алгоритм, ее решающий, – алгоритмом сортировки. С математической точки зрения алгоритм сортировки должен найти такую перестановку {аi1, . . . , аin} элементов множества, которая была бы согласована с заданным на нем отношением ≤ линейного порядка, т.е. для любых k, l из справедливости неравенства ik < il должно следовать аik ≤ аil

v0

v1 v0 v0

v2 v3 v1 v2 v1 v2

v4 v5 v3 v4 v3 v4 v5 v6

Рис. 4.17

Первоначально сортируемые элементы могут быть расположены в произвольном порядке, т.е. исходной может быть любая перестановка элементов сортируемого множества, и мы не имеем никакой априорной информации об этой перестановке. Единственный способ получить такую информацию – проводить попарные сравнения элементов аi, (относительно рассматриваемого линейного порядка) в какой-либо последовательности. Заметим, что при этом совершенно не обязательно проводить все возможные сравнения, т.е. сравнивать аi с аj для всех i ≠ j. Например, можно использовать транзитивность отношения порядка.

Все сравнения, которые в принципе могут быть проведены в процессе работы некоторого алгоритма, изображаются наглядно в виде ориентированного дерева, называемого деревом решений. На рис. 4.18 приведено дерево решений для трехэлементного множества {а, b, с}. Вершины ориентированного дерева, не являющиеся листьями, помечены проверяемыми неравенствами, а множество листьев находится во взаимно однозначном соответствии с множеством всех перестановок исходного множества.

Поскольку в результате сортировки может получиться любая перестановка исходного множества и каждой такой перестановке соответствует лист дерева решений, в общем случае количество листьев будет равно n! – количеству перестановок n-элементного множества.

Следовательно, сортируя входную последовательность, алгоритм обязательно пройдет какой-то путь от корня дерева решений к одному из листьев и, таким образом, число операций сравнения (число шагов алгоритма сортировки) будет величиной, пропорциональной высоте дерева решений, не меньшей чем log2n!, в силу теоремы 4.4. Используя для оценки факториала при больших n формулу Стирлинга

,

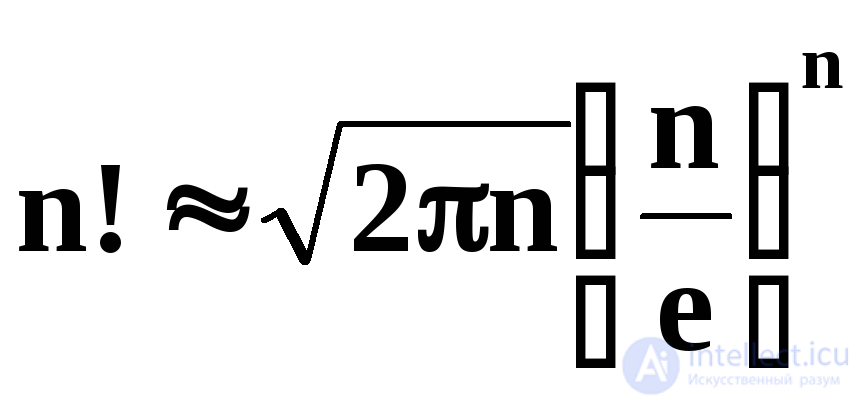получаем, что дерево решений имеет высоту порядка n log2n.

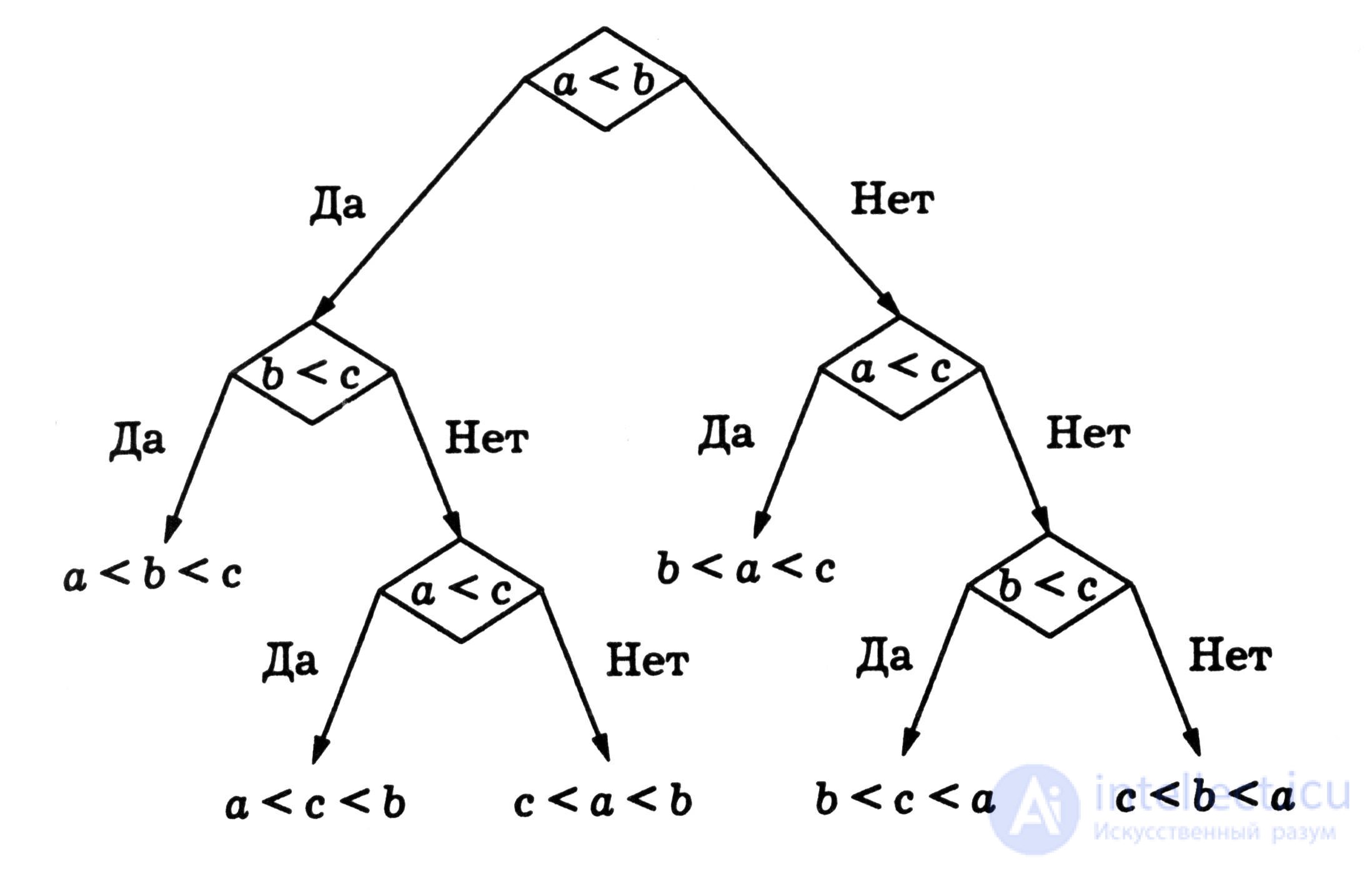
Рис. 4.18

Таким образом, в общем случае задачу сортировки с помощью попарных сравнений нельзя решить быстрее, чем за указанное число шагов. Безусловно, конкретный путь в дереве решений из корня к одному из листьев зависит от исходной перестановки. Например, в дереве решений, приведенном на рис. 4.18, есть два «коротких» пути длины 2, однако остальные пути имеют длину 3.

Заметим, что в общем случае ориентированное дерево – это не связный ориентированный граф. Компонентами ориентированного дерева являются его подграфы, порожденные множеством вершин, расположенных на некотором пути из корня в лист.

В заключение этой главы следует еще раз отметить, что графы являются одним из наиболее распространенных языков для представления разнообразных математических объектов и формулировки различных теоретических и прикладных задач, выходящих за пределы собственно теории графов. Трудно назвать прикладную область, где не применяется теория графов . Графы используются в математической логике и теории формальных систем, в теории алгоритмов и теоретическом программировании (для представления и анализа алгоритмов и программ), в теории языков и грамматик (для синтаксического анализа текстов). Они используются для описания и анализа как статических структур (организационных структур, транспортных сетей), так и динамических систем, в которых вершинам соответствуют состояния системы, а ориентированным ребрам – переходы из одного состояния в другое. Именно графы являются наиболее удобным средством формализованного представления конечных автоматов.

Контрольные задания

1. Сколько существует неориентированных графов с n вершинами?

2. Доказать, что сумма степеней всех вершин неориентированного графа равна удвоенному числу ребер ( это утверждение известно под названием «леммы о рукопожатиях»).

3. Установить, какие из изображенных на рис. 4.19 графов изоморфны, а какие нет

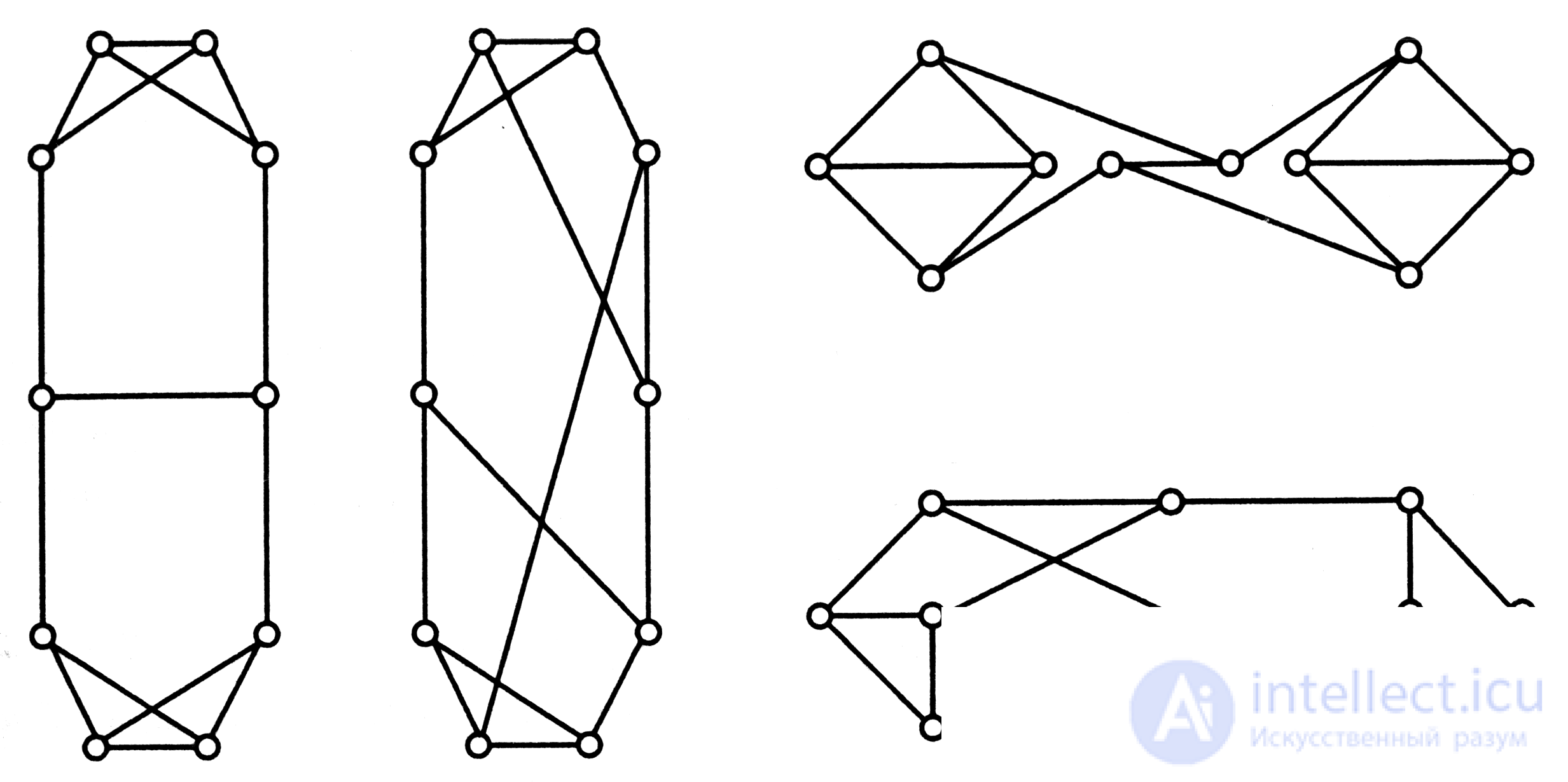
Рис. 4.19

4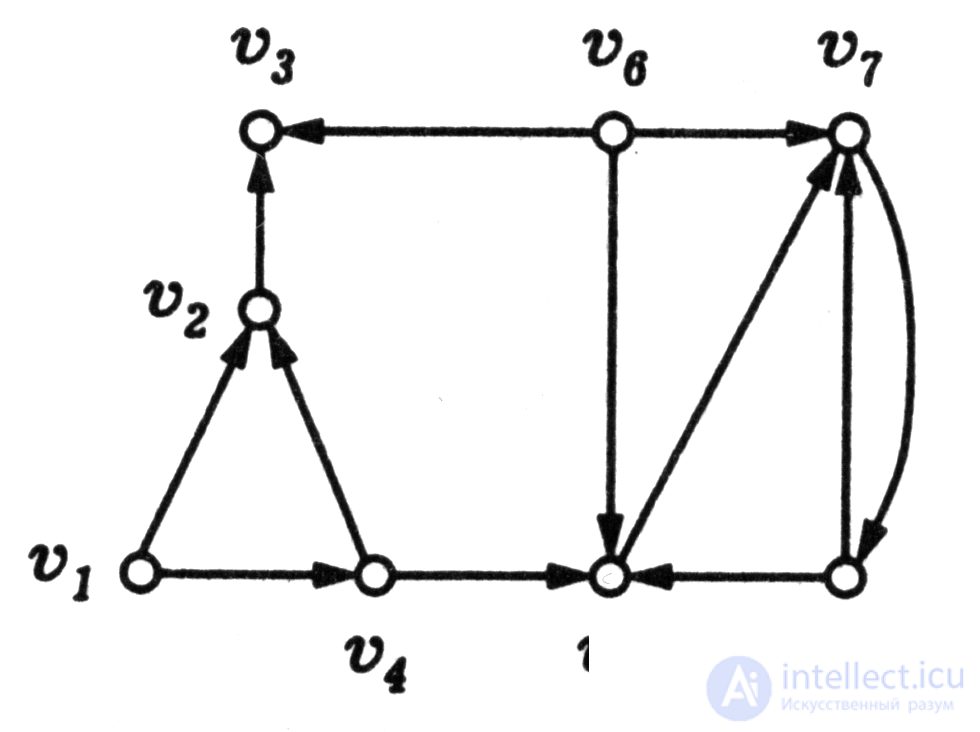. Найти все попарно неизоморфные графы неориентированные графы с четырьмя вершинами и тремя ребрами.

5. Установить, является ли ориентированный граф, изображенный на рис. 4.20, связным. Постройте матрицу смежности для этого графа.

6. Доказать, что связный неориентированный граф имеет эйлеров цикл тогда и только тогда, когда степень каждой его вершины четная. Рис. 4. 20

7. Инцидентор графа Р определен значениями: P(a,1,b); P(b,2,b); P(b,3,с); P(е,4,b); P(c,5,d); P(d,6,с); P(f,7,c); P(d,8, d); P(е,9,d); P(a,10,е); P(а,11,d); P(a,12,f) – которые истинны, остальные ложны. Построить граф, составить таблицы смежности и инцидентности, определить центр графа.

8. Ориентированный граф задан матрицей смежности, содержащей метки соответствующих ребер: построить граф и решить задачу о кратчайших путях.

0 7 8 9 10

0 0 8 9 10

0 -2 0 9 10

0 -4 -3 0 10

0 -7 -6 -5 0

9. Доказать, что ориентированный граф связный тогда и только тогда, когда в нем есть путь, проходящий через все вершины. Останется ли это утверждение справедливым, если потребовать, чтобы существовал простой путь.

10. Вычислите количество деревьев на множестве р вершин при р = 5;10;15;20. Сколько времени потребовалось бы для подсчета деревьев с производительностью 106 операций/с, считая одну операцию на дерево?

11. Покажите, что для деревьев на р вершинах при р < 5 центры и центроиды (или бицентры и бицентроиды) совпадают.

Анализ данных, представленных в статье про деревья как связанный граф, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое деревья как связанный граф, теория графов, деревья и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория конечных автоматов