Лекция
Привет, Вы узнаете о том , что такое логика буля, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое логика буля, булевы функции , настоятельно рекомендую прочитать все из категории Теория конечных автоматов.
Аппарат логики Буля, или иначе алгебры логики, оперирует с логическими переменными, которые могут принимать только два значения: 0 и 1. Логические переменные определяют некую логическую зависимость, которую принято называть булевой функцией. Множество всех булевых функций и операций над ними образует булеву алгебру или алгебру логики. булевы функции , или иначе функции алгебры логики (ФАЛ), могут принимать тоже только два взаимно исключающих значения 0 и 1. При формальном рассмотрении законов булевой алгебры логические переменные обычно обозначают строчными буквами латинского алфавита или присваивают им идентификаторы.
Логические величины 0 и 1 нельзя трактовать как числа, над ними нельзя производить арифметические действия, поскольку алгебра логики – это не алгебра чисел, а алгебра состояний. Тем не менее в булевой алгебре производятся логические действия над переменными, которые и определяют характер логических функций. Основные логические действия соответствуют простейшим операциям над множествами: инверсия, или отрицание, дизъюнкция, или логическое сложение, и конъюнкция, или логическое умножение. На основании этих трех логических действий строятся все сколь угодно сложные логические функции. При этом следует особо выделить функции одной и двух переменных, которые играют в алгебре Буля весьма важную роль. При помощи этих функций, используя принцип суперпозиции, можно описать любую логическую функцию любой сложности любого числа переменных.
Принцип суперпозиции заключается в том, что каждый аргумент логической функции может являться функцией других логических переменных, а именно: если есть функция f{x1;x2;x3}, то возможно, что x1 = (x4,x5).
Булевых функций одной переменной всего четыре.
Нулевая (const”0”) Ф = Х  =0 – значение функции равно нулю, каким бы ни было значение входной переменной.
=0 – значение функции равно нулю, каким бы ни было значение входной переменной.
Инверсия (не) Ф = – значение функции инверсно значению входной переменной.
– значение функции инверсно значению входной переменной.
Повторение (да) Ф = Х – значение функции повторяет значение входной переменной.
Единичная (const”1”) Ф = Х  = 1 – значение функции равно единице при любом значении входной переменной.
= 1 – значение функции равно единице при любом значении входной переменной.
Из всех функций двух переменных десять являются самостоятельными и зависят как от переменной а, так и от переменной b. Притом функции Y5 ,Y6 отличаются от соответствующих им Y7 ,Y8 лишь порядком расположения аргументов. Таким образом, лишь восемь из 16-ти булевых функций двух переменных являются оригинальными.
1. Y1 = a b –конъюнкция, логическое «и»;
–конъюнкция, логическое «и»;
2. Об этом говорит сайт https://intellect.icu . Y2 = a b 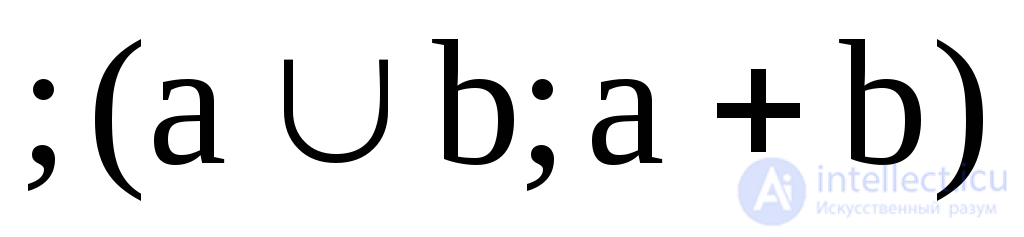 –дизъюнкция, логическое «или»;
–дизъюнкция, логическое «или»;
3. Y3 = a / b 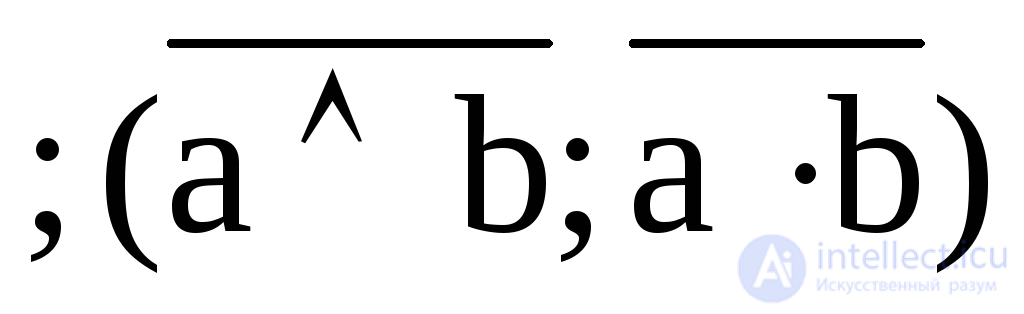 –штрих Шеффера, логическое «и-не»;
–штрих Шеффера, логическое «и-не»;
4. Y4 = a b 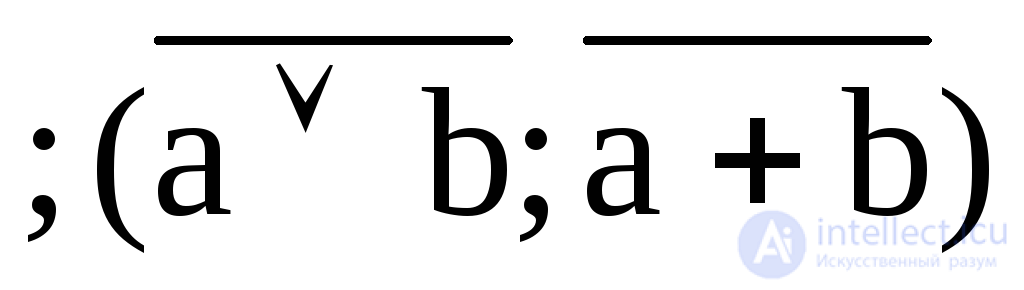 –стрелка Пирса (функция Вебба), «или - не»;
–стрелка Пирса (функция Вебба), «или - не»;
5. Y5 = a b  –запрет b, «а, но не b» ;
–запрет b, «а, но не b» ;
6. Y6 = a b 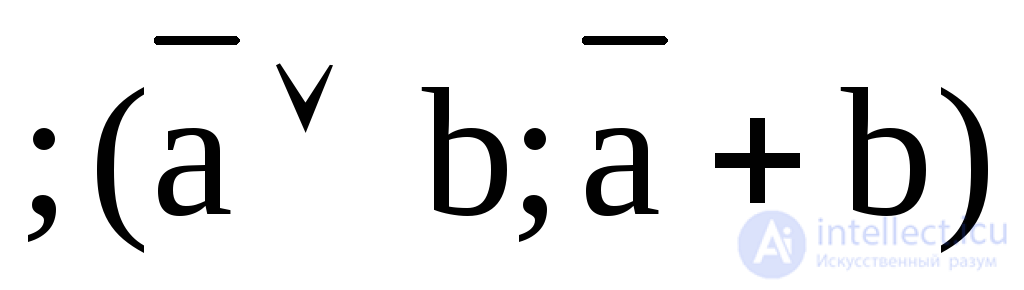 –импликация b, «если а, то b» ;
–импликация b, «если а, то b» ;
7. Y7 = b a 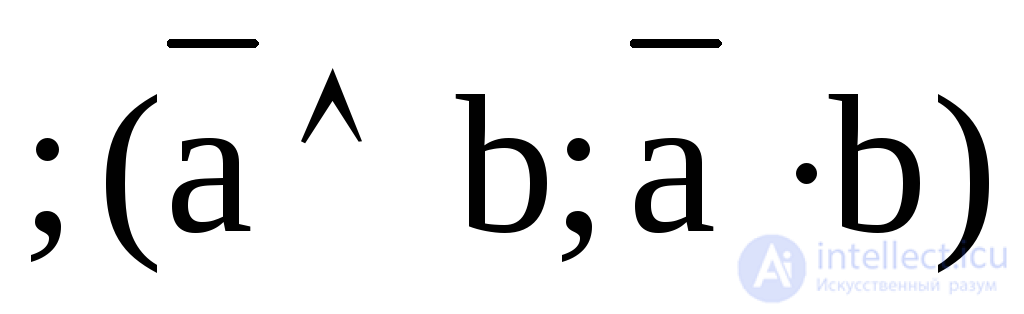 –запрет а, «b, но не а» ;
–запрет а, «b, но не а» ;
8. Y8 = b a 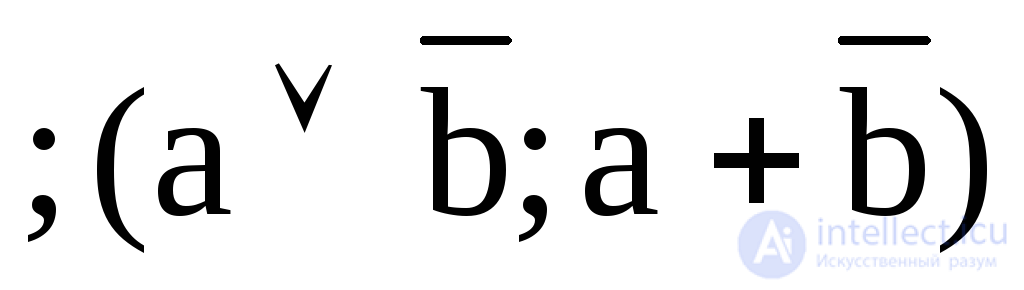 –импликация а, «если b, то а» ;
–импликация а, «если b, то а» ;
9. Y9 = a b 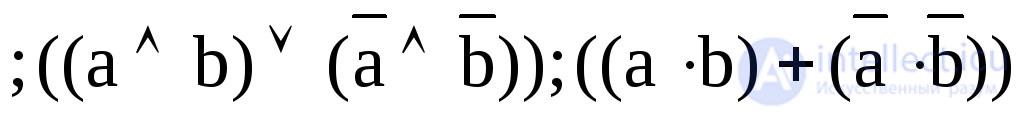 –эквивалентность,
–эквивалентность,
равнозначность;
10. Y10 = a b  –неравнозначность,
–неравнозначность,
«сумма по модулю 2».
Алгебра Буля, как любая математическая наука, базируется на нескольких аксиомах, или постулатах.
Если x ≠ 1, то 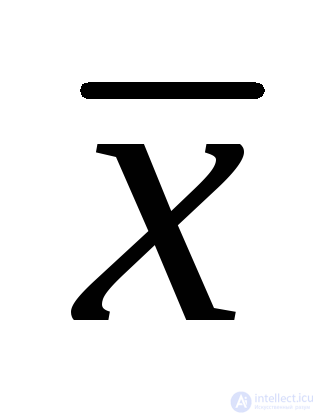 = 0; если x ≠ 0, то
= 0; если x ≠ 0, то 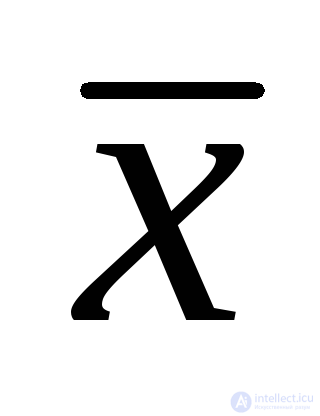 = 1 (аксиома взаимоисключения).
= 1 (аксиома взаимоисключения).
0 0 = 0; 0 0 = 0.
0 1 = 0; 0 1 = 1; (1 0 = 0; 1 0 = 1).
1 1 = 1; 1 1 = 1.
 ;
; 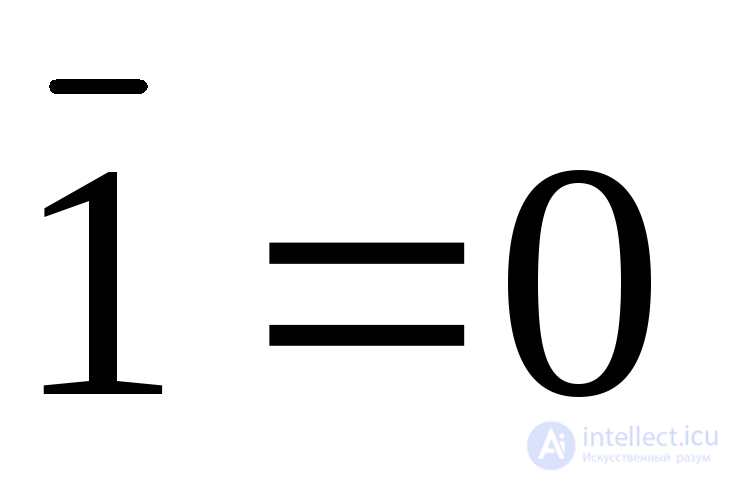 (инверсии).
(инверсии).
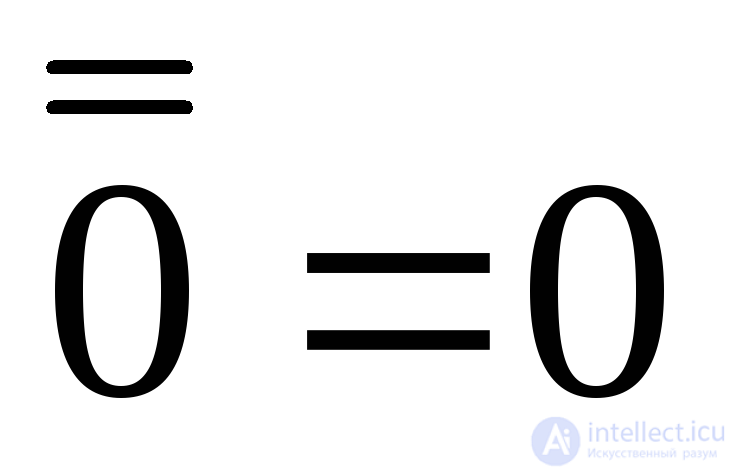 ;
;  (двойной инверсии).
(двойной инверсии).
В качестве основных законов алгебры Буля чаще других используют следующие (законы и теоремы приведены без доказательств).
1. Нулевого множества: 0 a = 0; 0 a b … x = 0;
0 a = 0; 0 a b … x = 0;
0 a = a
2. Универсального множества: 1 a = a; 

1 a = 1; 1 a b c … x = 1;
3. Идемпотентности (повторения): a a a … a = a;
a a a … a = a;
4. Дополнительности (противоречия): a  = 0;a
= 0;a  = 1;
= 1;
5. Двойной инверсии:  =a ;
=a ;
6. Коммутативности (переместительный): a b = b a;
a b = b a;
7. Ассоциативности (сочетательный): a (b c) = (a b) c;
a (b c) = (a b) c;
8. Дистрибутивности (распределительный): a (b c) = (a b) (a c);
a (b c) = (a b) (a c);
9. Поглощения: a (a b) = a;
a (a b) = a;
10. Склеивания: (a b) (a 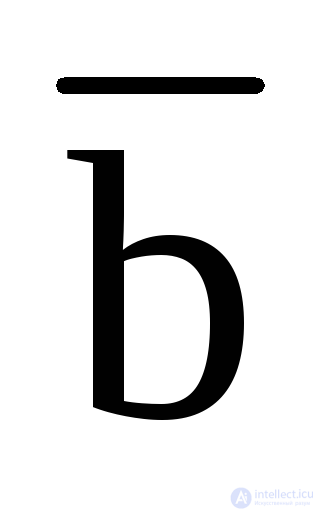 ) = a ;
) = a ;
(a b) (a 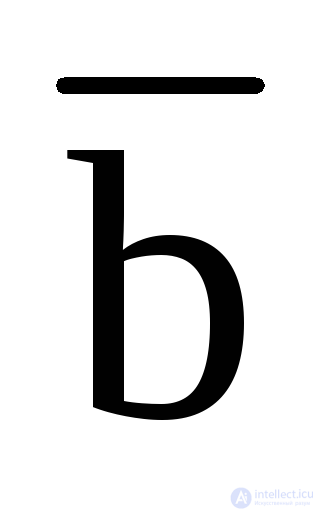 ) = a ;
) = a ;
a ( b) = a b ;
b) = a b ;
a ( b) = a b ;
b) = a b ;
11. Инверсии (теорема де Моргáнa): 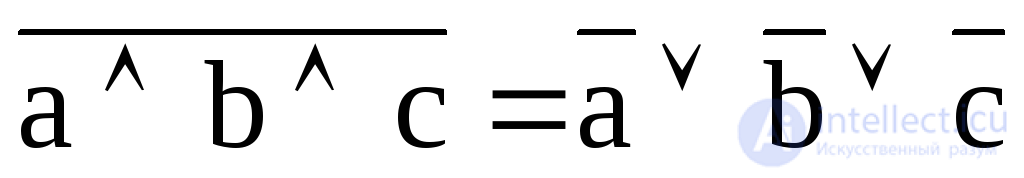 ;
;

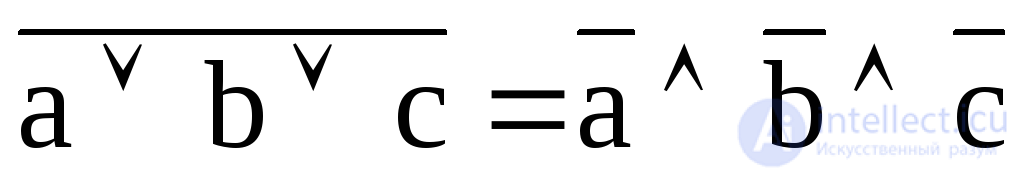 ;
;
12. Теорема Шеннона: для того, чтобы получить инверсию некоторой ФАЛ, необходимо взять инверсии переменных и заменить операции дизъюнкции на конъюнкции и наоборот:
если существует Y = f (a,b,c,...,x, , ), то  =f(
=f( ,
,
 ,…,
,…,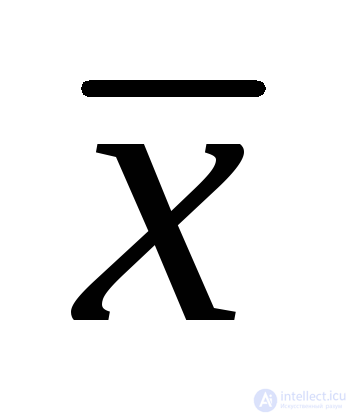 ,, )..
,, )..
13. Разложения: f (a,b,c,...,x) = [a f (1,b,c,...,x)] [ f (0,b,c,...,x)];
f (0,b,c,...,x)];
f (a,b,c,...,x) = [a f (0,b,c,...,x)] [ f (1,b,c,...,x)].
f (1,b,c,...,x)].
Законы и теоремы булевой алгебры необходимы для преобразования и упрощения логических функций, для доказательства тождественности и равносильности функций, а также для представления булевых функций в различных формах.
Анализ данных, представленных в статье про логика буля, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое логика буля, булевы функции и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория конечных автоматов
Из статьи мы узнали кратко, но содержательно про логика буля
Комментарии
Оставить комментарий
Теория конечных автоматов
Термины: Теория конечных автоматов