Лекция
Привет, Вы узнаете о том , что такое типы конечных автоматов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое типы конечных автоматов , настоятельно рекомендую прочитать все из категории Теория конечных автоматов.
В любом конечном автомате входные сигналы поступают в некоторой последовательности во времени, поэтому существует понятие входной последовательности. Аналогично определяетсявыходная последовательность.Зависимость выходной последовательности от входной последовательности будем называть условием работы конечного автомата.
Различают комбинационные ипоследовательностные автоматы. Длякомбинационных автоматов характерно то, что каждая совокупность состояний выходов (каждая входная последовательность) однозначно определяется одним или несколькими из конечного множества состояний входных переменных. При этом каждая выходная функция характеризуется определеннымикомбинациямивходов. В общем случае действие такого автомата можно описать некоторыми однозначными функциональными зависимостями между его входными и выходными переменными:
y1 = λ1(x1 ; x2 ; ... ; xm ) ,
y2 = λ2(x1 ; x2 ; ... ; xm ) ,
. . .
yn = λn(x1 ; x2 ; ... ; xm ) .
Пример: Пусть на входе имеются три переменныеx1 ; x2 ; x3. На выходе – две логические функцииy1, y2.
Допустим, что на входах имеем значения x1= 1,x2= 0,x3= 1, значения выходов при такой совокупности входов пусть будут –y1 = 1,y2= 0. Если автомат комбинационный, то изменение комбинации состояния его выходов (скажем,y1 = 0, y2= 0) возможно лишь в случае изменения состояния его входов (допустимx1= 1,x2= 0,x3= 0 илиx1= 0,x2= 0,x3=1). Т.е каждая комбинация выходов однозначно определена той или иной комбинацией входов. Тогда выходную функциюy1 можно выразить логическими выражениями (булевыми функциями), определенными только входными переменными,
y 1=x1 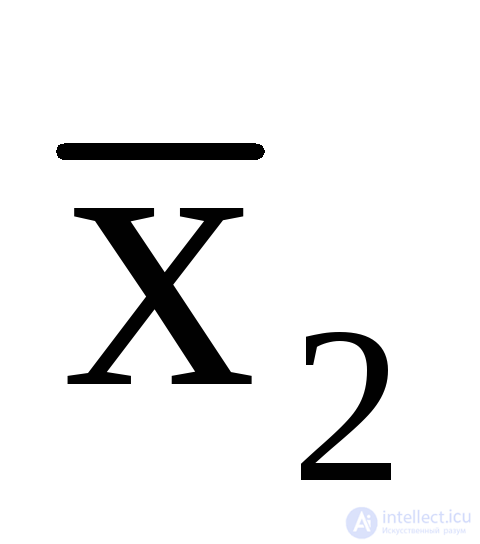 x3;
x3; 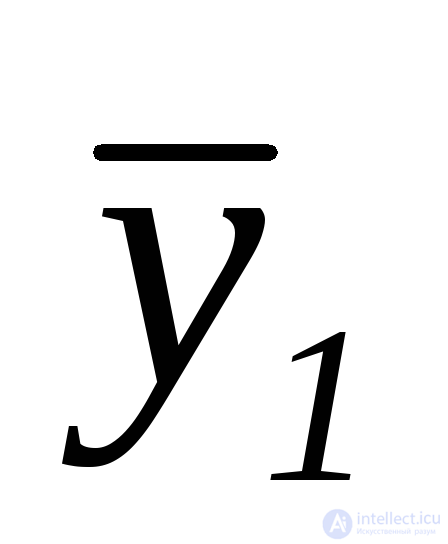 =x1
=x1 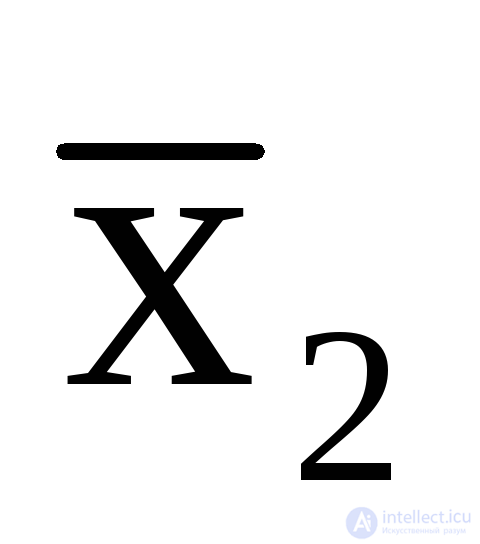
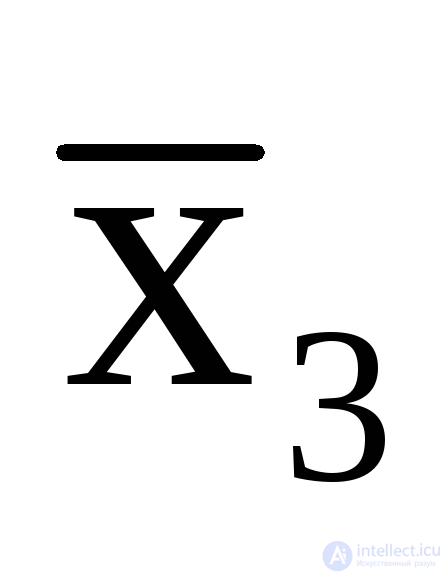
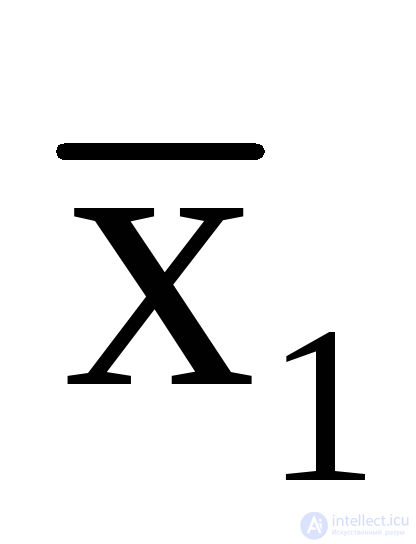
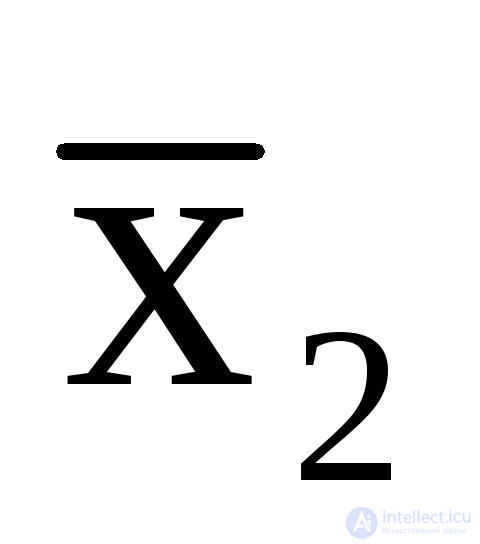 x3,
x3,
или представить таблицей истинности (табл. Об этом говорит сайт https://intellect.icu . 5.9).
Таблица 5.9
|
x1 |
x2 |
x3 |
y1 |
y2 |
|
1 |
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
Для комбинационных автоматов функция переходов не имеет смысла, поскольку в них отсутствуют каналы обратной связи (памяти), а внутренние состояния определены состоянием выходов. Функция выходов при этом вырождается к виду yv= λ(xv ).Такие автоматы называют еще автоматами без памяти илитривиальными автоматами.
Таблица 5.10 Таблица 5.11
|
.x1 |
x2 |
x3 |
y1 |
|
|
x1 |
x2 |
x3 |
z |
y1 |
|
1 |
0 |
0 |
0 |
|
|
1 |
0 |
0 |
0 |
0 |
|
… |
… |
… |
… |
|
|
… |
… |
… |
… |
… |
|
1 |
0 |
0 |
1 |
|
|
1 |
0 |
0 |
1 |
1 |
В последовательностныхавтоматах одна и та же совокупность состояний входных символов может в разные тактовые моменты цикла определять разные состояния выходных функций. Например, на одном из этапов циклаτvпри совокупности входовx1= 1,x2= 0,x3= 0 выходная функцияy1 = 0, а на каком-либо другом этапе циклаτv+iпри такой же совокупности входов выходная функцияy1 = 1 (табл. 5.10).
Таким образом, условия работы этого автомата противоречивы. Различные внутренние состояния автомата в этом случае определяются не только состояниями входов, но и последовательностьюприхода входных сигналов. Такой автомат не может быть построен без введения дополнительных внутренних переменных, кодирующих последовательность отработки тактов автомата, которые будем называть элементами памятиz (табл. 5.11) Переменная z является одновременно и функцией выхода, и входной переменной, однако не изменяет общее количество входных переменных и на блок-схеме автомата имеет вид обратной связи (рис 5.1б). В этом случае функцияy1 будет определена следующими логическими выражениями:
y1=x1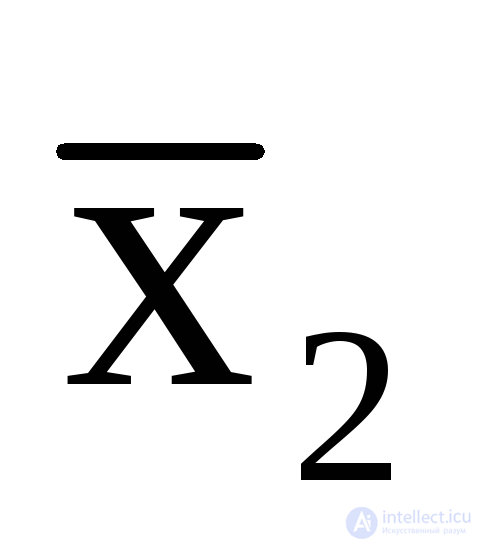
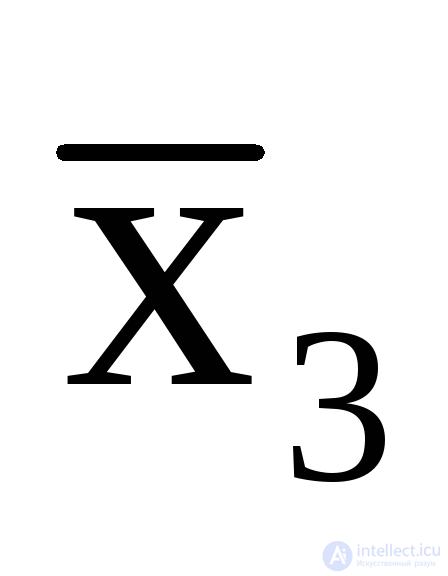
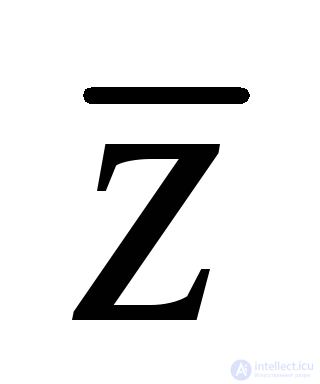 ,
,  =x1
=x1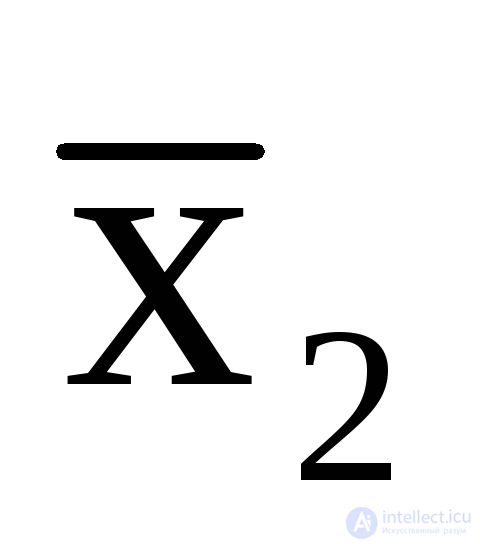
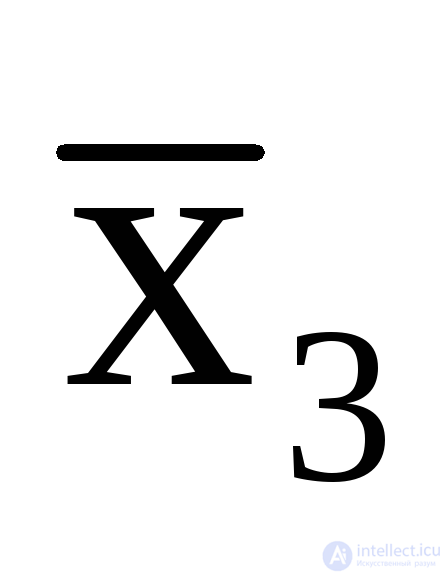 z.
z.
Как уже указывалось, наличие памяти zобусловливает внутренние состояния автоматаqv, которые, в свою очередь, определяют выходную функциюyvнаряду с состояниями входовxv. Для последовательностных автоматов характерно наличие и функции переходовδ,и функции выходов λ.
Если характеристические функции δиλопределены для всех возможных наборов из множества Х×Q, то такой автомат называют полностью определенным или полным, т.е.
( q Q) (
q Q) ( xХ) (δ(q, x ) ≠).
xХ) (δ(q, x ) ≠).
На практике встречаются случаи, когда не каждый символ входного алфавита может быть подан на автомат, находящийся в некотором внутреннем состоянии qv (ограничения на входе), или его выходы при некоторых входных воздействиях не представляют интереса или вообще не существуют (неопределенность выходов). В этом случае мы имеем дело снеполнымииличастичнымиавтоматами, и их таблицы выходов и переходов будут иметь некоторые незаполненные клетки.
Определение общей модели автомата, приведенное в конце раздела 5.1, связывают с автоматами первого рода, которые называют автоматамиМили. Если же функция выходов определяется только внутренними состояниями (состоянием элементов памяти), то мы имеем дело с автоматамивторого рода, называемыми автоматамиМура. Такие автоматы обычно моделируют вычислительные процессы. Функция выходов автомата Мура определяется только внутренними состояниямиyv= λ (qv,) и естественно является одноаргументной; ее обычно называют функцией отметок, поскольку каждому состоянию она однозначно ставит в соответствие отметку – выход. В графе переходов, отображающем автомат Мура, значение выхода записывается не на ребре, а при вершине (см. рис. 5.8а).
Анализ данных, представленных в статье про типы конечных автоматов, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое типы конечных автоматов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория конечных автоматов
Из статьи мы узнали кратко, но содержательно про типы конечных автоматов
Комментарии
Оставить комментарий
Теория конечных автоматов
Термины: Теория конечных автоматов