Лекция
Привет, сегодня поговорим про множество, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое множество, отношения множеств , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
множество — одно из ключевых понятий математики, в частности, теории множеств , компьютернных науках и логики.
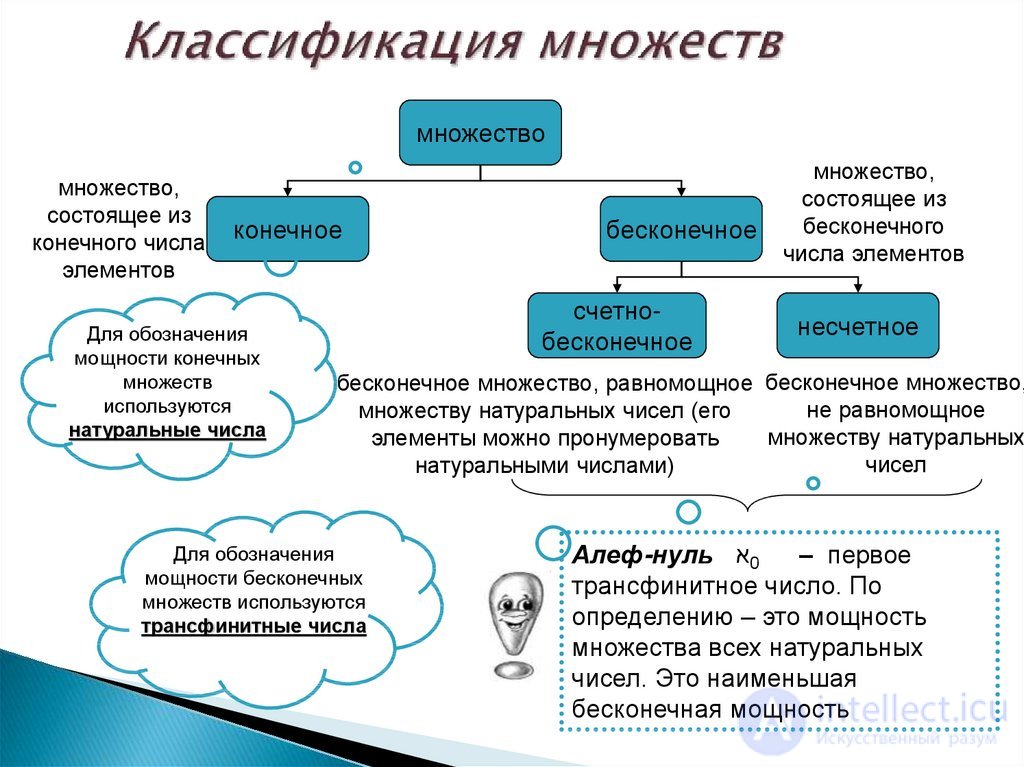
Понятие множества обычно принимается за одно из исходных (аксиоматических) понятий, то есть несводимое к другим понятиям, а значит, и не имеющееопределения; для его объяснения используются описательные формулировки, характеризующие множество как совокупность различных элементов, мыслимую как единое целое . Также возможно косвенное определение через аксиомы теории множеств. Множество может быть пустым и непустым, упорядоченным и неупорядоченным, конечным и бесконечным, бесконечное множество может быть счетным или несчетным. Более того, как в наивной, так и в аксиоматической теориях множеств любой объект обычно считается множеством.
Множество в компьютерных науках. Множество — тип и структура данных в информатике, которая является реализацией математического объекта множество.
Данные типа множество позволяют хранить ограниченное число значений определенного типа без определенного порядка. Повторение значений, как правило, недопустимо. За исключением того, что множество в программировании конечно, оно в общем соответствует концепции математического множества. Для этого типа в языках программирования обычно предусмотрены стандартные операции над множествами.
В зависимости от идеологии, разные языки программирования рассматривают множество как простой или сложный тип данных.
Основы теории конечных и бесконечных множеств были заложены Бернардом Больцано, который сформулировал некоторые из ее принципов.
С 1872 года по 1897 год (главным образом в 1872—1884 годы) Георг Кантор опубликовал ряд работ, в которых были систематически изложены основные разделы теории множеств, включая теорию точечных множеств и теорию трансфинитных чисел (кардинальных и порядковых). В этих работах он не только ввел основные понятия теории множеств, но и обогатил математику рассуждениями нового типа, которые применил для доказательства теорем теории множеств, в частности впервые к бесконечным множествам. Поэтому общепризнано, что теорию множеств создал Георг Кантор. В частности определил множество как «единое имя для совокупности всех объектов, обладающих данным свойством». Эти объекты назвал элементами множества. Множество объектов, обладающих свойством 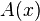 , обозначил
, обозначил  . Если некоторое множество
. Если некоторое множество 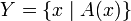 , то
, то 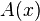 назвал характеристическим свойством множества
назвал характеристическим свойством множества 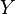 .
.
Эта концепция привела к парадоксам, в частности, к парадоксу Рассела.
Так как теория множеств фактически используется как основание и язык всех современных математических теорий в 1908 году теория множеств былааксиоматизирована независимо Бертраном Расселем и Эрнстом Цермело. В дальнейшем многие исследователи пересматривали и изменяли обе системы, в основном сохранив их характер. До сих пор они все еще известны как теория типов Рассела и теория множеств Цермело. Впоследствии теорию множеств Кантора стало принято называть наивной теорией множеств, а вновь построенную — аксиоматической теорией множеств.
В практике, сложившейся с середины XX века множество определяется как модель, удовлетворяющая аксиомам ZFC (аксиомы Цермело — Френкеля с аксиомой выбора). При таком подходе в некоторых математических теориях возникают совокупности объектов, которые не являются множествами. Такие совокупности называются классами (различных порядков).
Объекты, из которых состоит множество, называют элементами множества или точками множества. Множества чаще всего обозначают заглавными буквами латинского алфавита, его элементы — строчными. Если  — элемент множества
— элемент множества 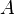 , то записывают
, то записывают 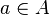 («
(« принадлежит
принадлежит 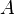 »). Если
»). Если  не является элементом множества
не является элементом множества 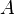 , то записывают
, то записывают 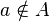 («
(« не принадлежит
не принадлежит 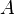 »). В отличие от мультимножества каждый элемент множества уникален, и во множестве не может быть двух идентичных элементов. Иначе говоря, добавление к множеству элементов, идентичных уже принадлежащим множеству, не меняет его:
»). В отличие от мультимножества каждый элемент множества уникален, и во множестве не может быть двух идентичных элементов. Иначе говоря, добавление к множеству элементов, идентичных уже принадлежащим множеству, не меняет его:
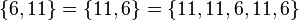 .
.

Отношение — математическая структура, которая формально определяет свойства различных объектов и их взаимосвязи. Распространенными примерами отношений в математике являются равенство (=), делимость, подобие, параллельность и многие другие.
Понятие отношения как подмножества декартова произведения формализовано в теории множеств и получило широкое распространение в языке математики во всех ее ветвях. Теоретико-множественный взгляд на отношение характеризует его с точки зрения объема — какими комбинациями элементов оно наполнено; содержательный подход рассматривается в математической логике, где отношение — пропозициональная функция, то есть выражение с неопределенными переменными, подстановка конкретных значений для которых делает его истинным или ложным. Важную роль отношения играют в универсальной алгебре, где базовый объект изучения раздела — множество с произвольным набором операций и отношений. Об этом говорит сайт https://intellect.icu . Одно из самых ярких применений техники математических отношений в приложениях — реляционные системы управления базами данных, методологически основанные на формальной алгебре отношений.
Отношения обычно классифицируются по количеству связываемых объектов (арность) и собственным свойствам, таким как симметричность, транзитивность, рефлексивность.
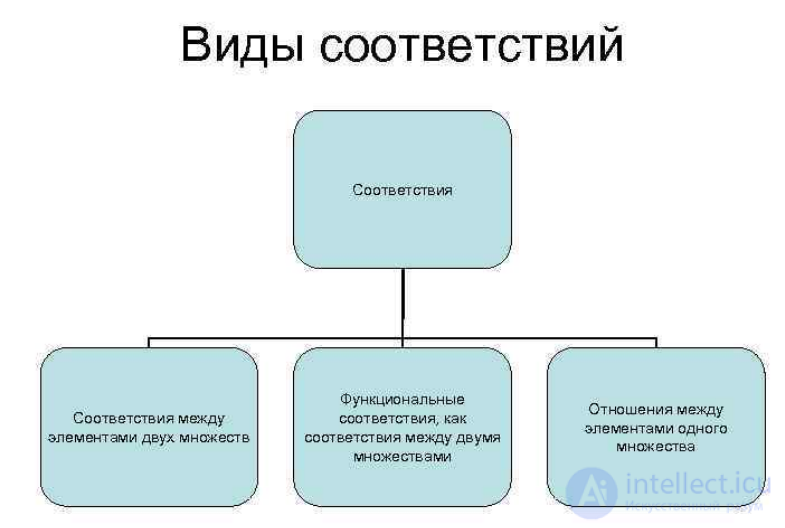
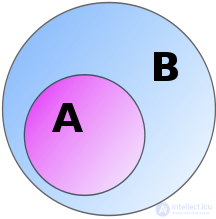
Диаграмма Венна для 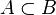
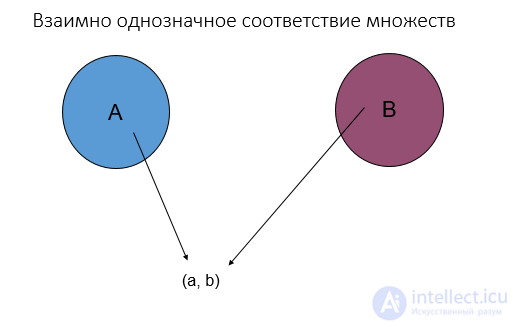
бинарное отношение множеств
Два множества 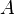 и
и 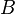 могут вступать друг с другом в различные отношения.
могут вступать друг с другом в различные отношения.
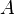 включено в
включено в 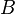 , если каждый элемент множества
, если каждый элемент множества 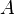 принадлежит также и множеству
принадлежит также и множеству 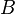 :
:
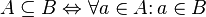
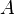 включает
включает 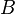 , если
, если 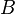 включено в
включено в 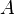 :
:
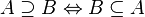
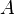 равно
равно 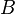 , если
, если 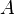 и
и 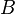 включены друг в друга:
включены друг в друга:
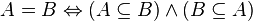
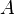 строго включено в
строго включено в 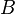 , если
, если 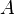 включено в
включено в 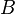 , но не равно ему:
, но не равно ему:
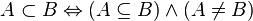
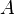 строго включает
строго включает 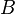 , если
, если 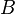 строго включено в
строго включено в 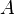 :
:

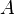 и
и 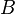 не пересекаются, если у них нет общих элементов:
не пересекаются, если у них нет общих элементов:
 и
и 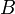 не пересекаются
не пересекаются 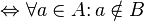
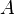 и
и 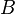 находятся в общем положении, если существует элемент, принадлежащий исключительно множеству
находятся в общем положении, если существует элемент, принадлежащий исключительно множеству 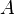 , элемент, принадлежащий исключительно множеству
, элемент, принадлежащий исключительно множеству 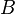 , а также элемент, принадлежащий обоим множествам:
, а также элемент, принадлежащий обоим множествам:
 и
и 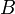 находятся в общем положении
находятся в общем положении 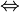

Свойства отношений
 R2), если любая пара (x, y), которая принадлежит отношению R1 также принадлежит и отношению R2
R2), если любая пара (x, y), которая принадлежит отношению R1 также принадлежит и отношению R2
2) Графический метод задания отношений множеств
a= {(a, d), (a, c), (b, b), (c, a), (e,d), (e, a)}
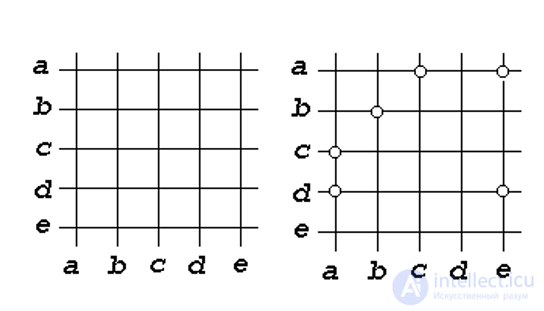
3)Графовое представление отношений множеств
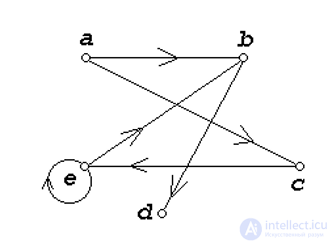


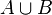

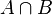
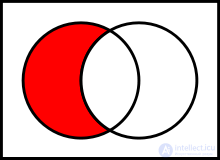
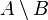
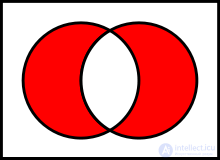
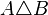
Основные бинарные операции, определяемые над множествами:
 .
.
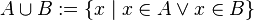 .
.
Если множества 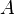 и
и 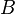 не пересекаются, то
не пересекаются, то 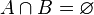 . Их объединение обозначают также:
. Их объединение обозначают также: 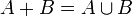 .
.
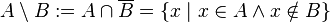 .
.
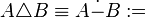
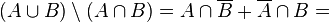
 .
.
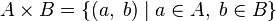 .
.
Для объяснения смысла операций часто используются диаграммы Венна, на которых представлены результаты операций над геометрическими фигурами как множествами точек.
Всякая система множеств, замкнутая относительно операций объединения и пересечения, образует относительно объединения и пересечения дистрибутивную решетку.
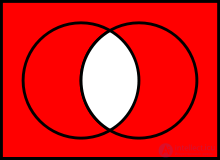
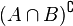
Дополнение определяется следующим образом:
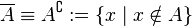 .
.
Операция дополнения подразумевает некоторый зафиксированный универсум (универсальное множество 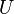 , которое содержит
, которое содержит 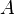 ), и сводится к разности множеств с этим универсумом:
), и сводится к разности множеств с этим универсумом:
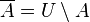 .
.
Система множеств с фиксированным универсумом, замкнутая относительно операций объединения, пересечения с введенным таким образом дополнением образует булеву алгебру.
Булеан — множество всех подмножеств:
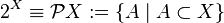 .
.
Обозначение 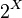 происходит из свойства мощности множества всех подмножеств конечного множества:
происходит из свойства мощности множества всех подмножеств конечного множества:
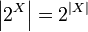 .
.
Булеан 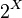 порождает систему множеств с фиксированным универсумом
порождает систему множеств с фиксированным универсумом 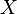 , замкнутую относительно операций объединения и пересечения, то есть, образует булеву алгебру.
, замкнутую относительно операций объединения и пересечения, то есть, образует булеву алгебру.
Сначала выполняются операции унарные операции (дополнение), затем — пересечения, затем — объединения и разности, которые имеют одинаковый приоритет. Последовательность выполнения операций может быть изменена скобками.
Мощность множества — характеристика множества, обобщающая понятие о количестве элементов для конечного множества таким образом, чтобы множества, между которыми возможно установление биекции были равномощны. Обозначается 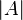 или
или  . Мощность пустого множества равна нулю, для конечных множеств мощность совпадает с числом элементов, для бесконечных множеств вводятся специальные кардинальные числа, соотносящиеся друг с другом по принципу включения (если
. Мощность пустого множества равна нулю, для конечных множеств мощность совпадает с числом элементов, для бесконечных множеств вводятся специальные кардинальные числа, соотносящиеся друг с другом по принципу включения (если 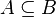 , то
, то 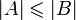 ) и распространением свойства мощности булеана конечного множества:
) и распространением свойства мощности булеана конечного множества: 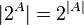 на случай бесконечных множеств (само обозначение
на случай бесконечных множеств (само обозначение 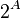 мотивировано этим свойством).
мотивировано этим свойством).
Наименьшая бесконечная мощность обозначается 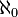 , это мощность счетного множества. Мощность континуума, биективного булеану счетного множества обозначается
, это мощность счетного множества. Мощность континуума, биективного булеану счетного множества обозначается  или
или 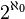 . Континуум-гипотеза — предположение о том, что между счетной мощностью и мощностью континуума нет промежуточных мощностей.
. Континуум-гипотеза — предположение о том, что между счетной мощностью и мощностью континуума нет промежуточных мощностей.
пример множеств чисел

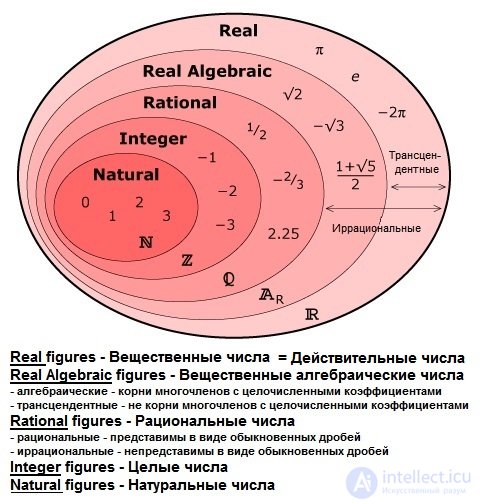
Под «множеством» мы понимаем соединение в некое целое M определенных хорошо различимых предметов m нашего созерцания или нашего мышления (которые будут называться «элементами» множества M).
Оригинальный текст (нем.)Unter einer ‚Menge‘ verstehen wir jede Zusammenfassung M von bestimmten wohlunterschiedenen Objecten m unsrer Anschauung oder unseres Denkens (welche die ‚Elemente‘ vonM genannt werden) zu einem Ganzen.
— Русский перевод — Кантор Г. Труды по теории множеств. — М.: Наука, 1985. — С. 173.. Немецкий оригинал — Georg Cantor. Beiträge zur Begründung der transfiniten Mengenlehre (нем.) // Mathematische Annalen. — 1895. — Т. 46. — С. 481.
Надеюсь, эта статья про множество, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое множество, отношения множеств и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.