Лекция
Привет, сегодня поговорим про гамильтонов граф, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое гамильтонов граф , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
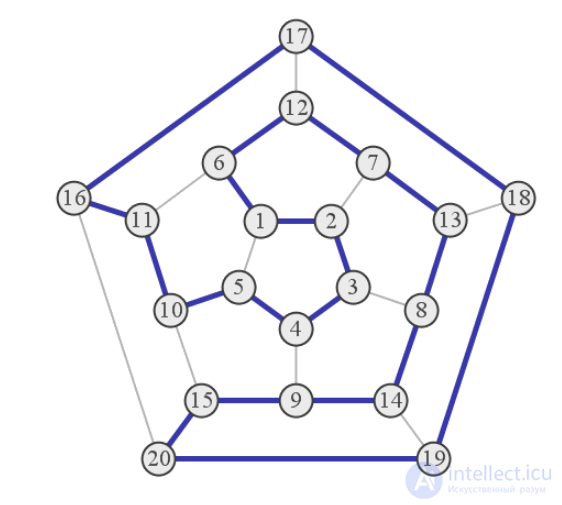
Гамильтонова линия для додекаэдра, предложенная Гамильтоном для замены его игры «вокруг света» на додекаэдре на задачу для плоского графа.
Гамильто́нов граф — математический объект теории графов. Представляет собой граф (набор точек и соединяющих их линий), который содержит гамильтонов цикл[1]. При этом гамильтоновым циклом является такой цикл (замкнутый путь), который содержит все вершины (точки) данного графа[2].
Также с гамильтоновым графом тесно связано понятие гамильтонова пути, который является простым путем (путем без петель), проходящим через каждую вершину графа ровно один раз[1]. Гамильтонов путь отличается от цикла тем, что у пути начальные и конечные точки могут не совпадать, в отличие от цикла. Гамильтонов цикл является гамильтоновым путем.
Гамильтоновы путь, цикл и граф названы в честь ирландского математика У. Гамильтона, который впервые определил эти классы , исследовав задачу «кругосветного путешествия» по додекаэдру. В этой задаче вершины додекаэдра символизировали известные города, такие как Брюссель, Кантон, Дели, Франкфурт и др., а ребра — соединяющие их дороги. Путешествующий должен пройти «вокруг света», найдя путь, который проходит через все вершины ровно один раз[3]. Чтобы сделать задачу более интересной, порядок прохождения городов устанавливался заранее. А чтобы было легче запомнить, какие города уже соединены, в каждую вершину додекаэдра был вбит гвоздь, и проложенный путь отмечался небольшой веревкой, которая могла обматываться вокруг гвоздя. Однако такая конструкция оказалась слишком громоздкой, и Гамильтон предложил новый вариант игры , заменив додекаэдр плоским графом, изоморфным графу, построенному на ребрах додекаэдра[4].
Необходимое условие существования гамильтонова пути в неориентированном графе: если неориентированный граф G содержит гамильтонов цикл, тогда в нем не существует ни одной вершины 
с локальной степенью 
. Доказательство следует из определения.
Условие Поша: Пусть граф G имеет 
вершин. Если для всякого 
, 
, число вершин со степенями большими или равными n меньше, чем n, и для нечетного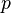 
число вершин со степенью 
не превосходит , то G —
гамильтонов граф . Об этом говорит сайт https://intellect.icu . Это достаточное условие не является необходимым[5].
Как следствие теоремы Поша, получаем более простые и менее сильные достаточные условия, найденные Дираком и Оре.
В 1952 году было сформулировано условие Дирака существования гамильтонова пути: пусть 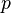— число вершин в данном графе и 
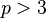; если степень каждой вершины не меньше, чем 
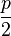, то данный граф — гамильтонов[6].
Теорема Оре
Условие Оре: пусть 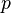— количество вершин в данном графе и . Если для любой пары несмежных вершин 
выполнено неравенство 
, то данный граф — гамильтонов (другими словами: сумма степеней любых двух несмежных вершин не меньше общего числа вершин в графе)[6].
Теорема Бонди-Хватала обобщает утверждения Дирака и Оре. Для графа G с n вершинами замыкание определяется добавлением в G ребра (u,v) для каждой пары несмежных вершин u и v, сумма степеней которых не меньше n[7] (другими словами: граф является гамильтоновым тогда и только тогда, когда его замыкание — гамильтонов граф).
При прямом переборе вариантов вершин возможно значительное увеличение средней сложности поиска гамильтонова пути на случайных графах (если гарантируется наличие гамильтонова пути в графе). Для улучшения данного способа можно на каждом шаге перебора при некоторой построенной части цепи проверять, образуют ли оставшиеся вершины связный граф (если не образуют, то цепь не может являться началом гамильтоновой цепи); на каждом шаге перебора при выборе следующей вершины пробовать сначала вершины с наименьшей остаточной степенью (количеством ребер, ведущих в еще не посещенные вершины). Кроме того, если это дерево является цепью, то гамильтонов цикл в нем возможен. Иначе (если в дереве есть вершины степенью не меньше, чем 3) построение гамильтонова цикла невозможно.
Гамильтонов цикл используется в системе так называемых протоколов с нулевым разрешением.
Пусть Марк и Вадим знают один и тот же гамильтонов граф G, причем Марк знает в нем гамильтонов цикл. Он хочет доказать это Вадиму, не раскрывая ему самого цикла. Существует алгоритм того, как он должен действовать[8]:
1. Марк случайным образом преобразовывает граф G. Передвигая точки и изменяя их метки, он создает новый граф H, топологически изоморфный G. Тогда, зная гамильтонов цикл в G, он легко найдет его в H. Если он не сам создает H, то определение изоморфизма между графами является слишком сложной задачей, решение которой требует огромного количества времени. Затем он шифрует H и получает граф H/ .
2. Марк передает Вадиму H/ .
3. Вадим просит Марка либо:
4. Марк выполняет его просьбу. Он либо:
5. Марк и Вадим повторяют этапы 1 — 4 n раз.
Если Марк не обманывает, то он сможет рассказать Вадиму одно из доказательств на этапе 3. Однако, если гамильтонов цикл для G ему самому неизвестен, он не сможет создать H/, удовлетворяющий обоим доказательствам. Правда, Марк может создать или граф изоморфный G, или граф с таким же числом вершин и ребер и правильным гамильтоновым циклом. И, хотя с вероятностью 50 % он может угадать, какое доказательство попросит Вадим на этапе 3, Вадим может повторить протокол достаточное число раз, пока не убедится, что Марк знает гамильтонов цикл в G.
Коммивояжеру необходимо посетить каждый город в пределах некоторой территории и возвратиться в пункт отправления. Требуется, чтобы путь был как можно короче. Таким образом, исходная задача преобразуется в задачу поиска минимальной протяженности (длительности или стоимости)[9].
Задачу можно переформировать в терминах теории графов — построить такой граф G(X, A), вершины которого соответствуют городам, а ребра — коммуникации между городами. Решение этой задачи ищут среди гамильтоновых циклов построенного графа.
Известно много способов решения этой задачи. Можно выделить методы, разработанные Беллмором и Немхаузером[10], Гарфинкелем и Немхаузером[11], Хелдом и Карпом[12], Стекханом[13]. Также известными решениями задачи коммивояжера являются метод ветвей и границ и метод последовательного улучшения решения[14].
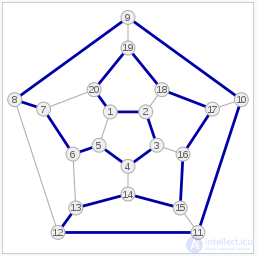
Граф додекаэдра с выделенным циклом Гамильтона
Полугамильтоновым[15] графом называется граф, содержащий простую цепь, проходящую через каждую его вершину. При этом, всякий гамильтонов граф является полугамильтоновым. Гамильтонов цикл является простым остовным циклом[16].
Суть задачи о гамильтоновом цикле — выяснить, имеет ли заданный граф G гамильтонов цикл. Данная задача являетсяNP-полной[17].
Гамильтонова орцепь орграфа[18] — простая цепь, проходящая через каждую вершину орграфа ровно один раз.
Гамильтоновым орциклом[18] называется орцикл[18] орграфа, который проходит через каждую его вершину, называется.
Орграф называется полугамильтоновым[18], если он имеет гамильтонову орцепь, и гамильтоновым[18], если обладает гамильтоновым орциклом.
На этом все! Теперь вы знаете все про гамильтонов граф, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое гамильтонов граф и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.