Матрица смежности — один из способов представления графа в виде матрицы.

Определение [править ]

Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элементаa_ij равно числу ребер из i-й вершины графа в j-ю вершину.

Иногда, особенно в случае неориентированного графа, петля (ребро из i-й вершины в саму себя) считается за два ребра, то есть значение диагонального элемента a_ii в этом случае равно удвоенному числу петель вокруг i-й вершины.

Матрица смежности простого графа (не содержащего петель и кратных ребер) является бинарной матрицей и содержит нули на главной диагонали.

Примеры[править ]

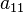• Ниже приведен пример неориентированного графа и соответствующей ему матрицы смежности A. Этот граф содержит петлю вокруг вершины 1, при этом в зависимости от конкретных приложений элемент  может считаться равным либо одному (как показано ниже), либо двум.

Граф	Матрица смежности

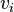• a_ij — число ребер, связывающих вершины  и 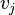, причем в некоторых приложениях каждая петля (ребро  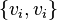при некотором ) учитывается дважды.

• Матрица смежности пустого графа, не содержащего ни одного ребра, состоит из одних нулей.

Свойства[править ]

Матрица смежности неориентированного графа симметрична, а значит обладает действительными собственными значениями и ортогональным базисом из собственных векторов. Набор ее собственных значений называется спектром графа, и является основным предметом изучения спектральной теории графов.

Два графа G₁ и G₂ с матрицами смежности A₁ и A₂ являются изоморфными если и только если существует перестановочная матрица P, такая что

PA₁P^-1 = A₂.

Из этого следует, что матрицы A₁ и A₂ подобны, а значит имеют равные наборы собственных значений, определители и характеристические многочлены. Однако обратное утверждение не всегда верно — два графа с подобными матрицами смежности могут быть неизоморфны.

Степени матрицы[править ]

Если A — матрица смежности графа G, то матрица A^m обладает следующим свойством: элемент в i-й строке, j-м столбце равен числу путей из i-й вершины в j-ю, состоящих из ровно m ребер.

Структура данных[править ]

Матрица смежности и  списки смежности  являются основными структурами данных, которые используются для представления графов в компьютерных программах

Использование матрицы смежности предпочтительно только в случае неразреженных графов, с большим числом ребер, так как она требует хранения по одному биту данных для каждого элемента. Если граф разрежен, то большая часть памяти напрасно будет тратиться на хранение нулей, зато в случае неразреженных графов матрица смежности достаточно компактно представляет граф в памяти, используя примерно   бит памяти, что может быть на порядок лучше списков смежности.

В алгоритмах, работающих со взвешенными графами (например, в алгоритме Флойда-Уоршелла), элементы матрицы смежности вместо чисел 0 и 1, указывающих на присутствие или отсутствие ребра, часто содержат веса самих ребер. При этом на место отсутствующих ребер ставят некоторое специальное граничное значение (англ. sentinel), зависящее от решаемой задачи, обычно 0 или .

Вау!! 😲 Ты еще не читал? Это зря![править ]