Лекция
Привет, Вы узнаете о том , что такое клика, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое клика , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
Кликой неориентированного графа называется подмножество его вершин, любые две из которых соединены ребром. Клики являются одной из основных концепций теории графов и используются во многих других математических задачах и построениях с графами. Клики изучаются также в информатике — задача определения, существует ли клика данного размера в графе (Задача о клике) является NP-полной. Несмотря на эту трудность, изучаются многие алгоритмы для поиска клик.
Хотя изучение полных подграфов началось еще с формулировки теоремы Рамсея в терминах теории графов Эрдешем и Секерешем . Термин «клика» пришел из работы Люка и Пери , использовавших полные подграфы при изучении социальных сетей для моделировании клик людей, то есть групп людей, знакомых друг с другом . Клики имеют много других приложений в науке, и, в частности, в биоинформатике.
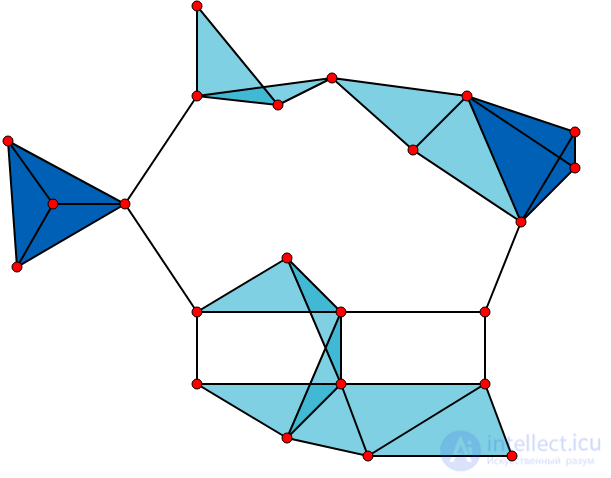
Граф с 23 кликами, содержащими 1 вершину (вершины графа), 42 кликами, состоящими из 2 вершин (ребра графа), 19 кликами, состоящими из 3 вершин (закрашенные треугольники) и двумя кликами, состоящими из 4 вершин (темно-синие области).
Шесть ребер не входят ни в один треугольник и 11 светло-голубых треугольников образуют максимальные клики.
Две темно-синие 4-клики являются как наибольшими, так и максимальными, и кликовое число графа равно 4.
Кликой в неориентированном графе называется подмножество вершин
, такое что для любых двух вершин в
существует ребро, их соединяющее. Это эквивалентно утверждению, что подграф, порожденный
, является полным.
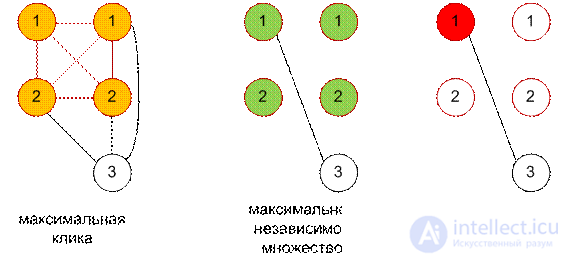
Максимальная клика или клика, максимальная по включению — это клика, которую нельзя расширить добавлением в нее вершин. Иначе говоря, в данном графе нет клики большего размера, в которую она входит.
Наибольшая клика или клика, максимальная по размеру — это клика максимального размера для данного графа.
Кликовое число графа
— это число вершин в наибольшей клике графа
. Число пересечений графа
— это наименьшее число клик, вместе покрывающих все ребра графа
.
Противоположное клике понятие — это независимое множество в том смысле, что каждая клика соответствует независимому множеству в дополнительном графе. Задача о покрытии кликами состоит в нахождении как можно меньшего числа клик, содержащих все вершины графа.
Связанный термин — это биклика, полный двудольный подграф. Двудольная размерность графа — это минимальное число биклик, необходимых для покрытия всех ребер графа.
Математические результаты относительно клик включают следующие.
Некоторые важные классы графов можно определить их кликами:
Кроме того, многие другие математические построения привлекают клики графов. Среди них:
Близкая концепция к полным подграфам — это разбиения графов на полные подграфы и полные миноры графа. В частности, теорема Куратовского и теорема Вагнера характеризуют планарные графы путем запрещения полных и полных двудольных подграфов и миноров, соответственно.
В информатике задача о клике — это вычислительная задача нахождения максимальной клики или клик в заданном графе. Задача является NP-полной, одной из 21 NP-полных задач Карпа . Она также сложна для параметрического приближения и трудно аппроксимируема. Тем не менее разработано много алгоритмов для работы с кликами, работающих либо за экспоненциальное время (такие как алгоритм Брона — Кербоша), либо специализирующиеся на семействах графов, таких как планарные графы или совершенные графы, для которых задача может быть решена за полиномиальное время.
Ниже приведен список свободно распространяемого программного обеспечение для поиска максимальной клики.
| Название | Лицензия | Язык API | Короткое описание |
|---|---|---|---|
| NetworkX | BSD | Python | приближенное решение, смотри процедуру max_clique (недоступная ссылка) |
| maxClique | CRAPL | Java | точные алгоритмы, реализации DIMACS |
| OpenOpt | BSD | Python | точные и приближенные решения, возможность указать ребра, которые должны быть включены (MCP) |
Задача о клике относится к классу NP-полных задач в области теории графов. Впервые она была сформулирована в 1972 году Ричардом Карпом.

Кликой в неориентированном графе называется подмножество вершин, каждые две из которых соединены ребром графа. Иными словами, это полный подграф первоначального графа. Размер клики определяется как число вершин в ней. Задача о клике существует в двух вариантах: в задаче распознавания требуется определить, существует ли в заданном графе G клика размера k, в то время как в вычислительном варианте требуется найти в заданном графе G клику максимального размера.
NP-полнота задачи о клике следует из NP-полноты задачи о независимом множестве вершин. Легко показать, что необходимым и достаточным условием для существования клики размера k является наличие независимого множества размера не менее k в дополнении графа. Это очевидно, поскольку полнота подграфа означает, что его дополнение не содержит ни одного ребра.
Другое доказательство NP-полноты можно найти в книге «Алгоритмы: построение и анализ».
Как и для других NP-полных задач, эффективного алгоритма для поиска клики заданного размера на данный момент не найдено. Полный перебор всех возможных подграфов размера k с проверкой того, является ли хотя бы один из них полным, — неэффективен, поскольку полное число таких подграфов в графе с v вершинами равно биномиальному коэффициенту
Другой алгоритм работает так: две клики размера n и m «склеиваются» в большую клику размера n+m, причем кликой размера 1 полагается отдельная вершина графа. Алгоритм завершается, как только ни одного слияния больше произвести нельзя. Время работы данного алгоритма линейно, однако он является эвристическим, поскольку не всегда приводит к нахождению клики максимального размера. В качестве примера неудачного завершения можно привести случай, когда вершины, принадлежащие максимальной клике, оказываются разделены и находятся в кликах меньшего размера, причем последние уже не могут быть «склеены» между собой.
Теорема Кенига. В двудольном графе размер максимального паросочетания равен размеру минимального вершинного покрытия.
Из теоремы Кенига следует, что
размер максимальной клики =
размер максимального независимого множества в дополняющем графе =
количество вершин графа – размер минимального вершинного покрытия =
количество вершин графа – размер максимального паросочетания в дополняющем графе
Пример
Рассмотрим второй пример. Размер максимальной клики графа равен 4. Размер максимального независимого множества в дополняющем графе равен 4.
Много различных задач биоинформатики смоделированы с помощью клик. Например, Бен-Дор, Шамир и Яхини[10] моделировали задачу разбиения на группы экспрессии генов, как задачу поиска минимального числа изменений, необходимых для преобразования графа данных в граф, сформированный несвязными наборами клик. Танай, Шаран и Шамир[11] обсуждают похожую задачу бикластеризации данных экспрессии генов, в которой кластеры должны быть кликами. Сугихара использовал клики для моделирования экологических ниш в пищевых цепях. Дей и Санков описывают задачу описания эволюционных деревьев, как задачу нахождения максимальных клик в графе, в котором вершины представляют характеристики, а две вершины соединены ребром, если существует идеальная история развития , комбинирующая эти две характеристики. Самудрала и Молт моделировали предсказание структуры белка как задачу нахождения клик в графе, вершины которого представляют позиции частей белка, а путем поиска клик в схеме взаимодействия белок-белок , Спирит и Мирни нашли кластеры белков, которые взаимодействуют тесно друг с другом и имеют слабое взаимодействие вне кластера. Анализ мощности графа — это метод упрощения сложных биологических систем путем нахождения клик и связанных структур в этих системах.
В электротехнике Прихар использовал клики для анализа коммуникационных сетей, а Паул и Унгер использовали их для разработки эффективных схем для вычисления частично определенных булевских функций. Клики используются также в автоматических генерациях тестовых шаблонов — большая клика в графе несовместимости возможных дефектов дает нижнюю границу множества тестовов . Конг и Смит описывают применение клик для поиска иерархических структур в электрических схемах.
В химии Родес и соавторы использовали клики для описания химических соединений в химической базе данных , имеющих высокую степень похожести. Кул, Крипен и Фризен использовали клики для моделирования позиций, в которых два химических соединения связываются друг с другом.
Исследование, описанное в статье про клика, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое клика и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.