Рёберный граф (производный графом , покрывающий граф)

Привет, сегодня поговорим про рёберный граф , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое рёберный граф , производный граф, покрывающий граф , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

В теории графов реберным графом L(G) неориентированного графа G называется граф L(G), представляющий соседство ребер графа G.

Понятие реберного графа для данного графа настолько естественно, что независимо было введено многими авторами. Конечно, каждый из них давал свое название: Оре назвал этот граф «смежностным графом», Сабидусси — «графом производной», Байнеке — «производным графом», Сешу и Рид — «реберно-вершинно-двойственным», Кастелейн — «покрывающим графом», Менон — «присоединенным» («сопряженным») .

Одна из наиболее ранних и наиболее важных теорем о реберных графах принадлежит Уитни, который доказал, что за одним исключением структура графа Gполностью определяется реберным графом. Другими словами, за одним исключением, весь граф может быть восстановлен из реберного графа.

Формальное определение

Пусть задан граф G, тогда его реберный граф L(G) — это такой граф, что

• любая вершина графа L(G) представляет ребро графа G
• две вершины графа L(G) смежны тогда и только тогда, когда их соответствующие ребра имеют общую вершину («смежны») в G.

Примеры

Пример построения

Следующий рисунок показывает граф (слева, с синими вершинами) и его реберный граф (справа, с зелеными вершинами). Каждая вершина реберного графа помечена парой номеров вершин соответствующего ребра в исходном графе. Например, зеленая вершина справа с меткой 1,3 соответствует ребру слева между голубыми вершинами 1 и 3. Зеленая вершина 1,3 смежна трем другим зеленым вершинам: 1,4, 1,2 (соответствующей ребрам с общей вершиной 1 в синем графе) и 4,3 (соответствующей ребрам с общей вершиной 3 в синем графе).

Хордальные графы

Реберный граф полного графа Kn известен как хордальный граф (или триангулированный граф). Важной теоремой о хордальных графах является теорема, утверждающая, что хордальный граф характеризуется спектром, за исключением n = 8, когда имеется три других графа с тем же спектром, что и у L(K8). Исключения объяснены в переключении графов.

Реберные графы выпуклых многогранников

Источник примеров реберных графов можно найти в геометрии — для графов простых многогранников. Если построить реберный граф для графа тетраэдра получим граф октаэдра. Из графа куба получим граф кубооктаэдра. Из графа додекаэдра получим граф икосододекаэдра, и т.д.. Геометрически операция состоит в отсечении всех вершин многогранника плоскостью, пересекающей все ребра, сопряженные с вершиной, в их середине.

Если многогранник не простой (то есть имеет больше трех граней на вершину) реберный граф не будет плоским.

Срединный граф

Срединный граф — это вариант реберного графа для плоского графа. В срединном графе две вершины смежны в том, и только в том случае, когда соответствующие ребра исходного графа являются двумя последовательными ребрами некоторой области плоского графа. Для простых многоугольников срединный граф и реберный граф совпадают, но для сложных многоугольников срединный граф остается плоским. Так, срединные графы куба и восьмигранника изоморфны графу кубооктаэдра, а срединные графы двенадцатигранника и икосаэдра изоморфны графу икосододекаэдра.

Свойства

Свойства графа G, зависящие только от смежности ребер могут быть переведены в эквивалентные свойства графа L(G), зависящие только от смежности вершин. Например, паросочетание в G — это множество дуг, ни одна из которых не смежна другой, и соответствующее множество вершин в L(G), ни одна из которых не смежна другой, то есть, Независимое множество вершин.

Итак,

• Реберный граф связного графа связен. Об этом говорит сайт https://intellect.icu . Если G связен, он содержит путь, соединяющий любые два его ребра, что переводится в путь графа L(G), содержащий любые две вершины графа L(G). Тем не менее, графу G, содержащему изолированные вершины, а посему несвязному, может соответствовать связный реберный граф.
• Задача о максимальном независимом множестве для реберного графа соответствует задаче нахождения максимального паросочетания в исходном графе.

Поскольку максимальное паросочетание может быть найдено за полиномиальное время, то и максимальное независимое множество реберного графа может быть найдено за полиномиальное время вопреки трудности поиска такого множества для более общих семейств графов.

• Реберное хроматическое число графа G равно вершинному хроматическому числу его реберного графа L(G).
• Реберный граф реберно-транзитивного графа является вершинно-транзитивным графом.
• Если граф G имеет Эйлеров цикл, то есть G связен и имеет четное число ребер в каждое вершине, то его реберный граф является Гамильтоновым графом. (Однако не все Гамильтоновы циклы в реберном графе получаются из Эйлеровских циклов.)
• Реберный граф не имеет клешней, то есть порожденных подграфов в виде трех листьев.
• Реберный граф дерева является блоковым графом без клешней.

Характеристики и распознавание

Девять минимальных нереберных графов, из характеристик Байнеке (Beineke) запрещенных подграфов реберных графов. Граф является реберным тогда и только тогда, когда он не содержит ни один их этих девяти графов в качестве порожденного подграфа.

Граф G является реберным графом какого-либо другого графа в том и только в том случае, когда можно найти наборклик в G, разбивающих дуги графа G так, что каждая вершина G принадлежит в точности двум кликам. Может случиться, что для достижения этого потребуется отдельные вершины выделить в клики. По теореме Уитни [10][11], еслиG не является треугольником, может быть только одно разбиение такого рода. Если разбиение существует, мы можем построить граф, для которого G будет реберным графом путем создания вершины для каждой клики и соединением полученных вершин ребром, если вершина принадлежит обоим кликам. Таким образом, за исключением 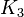и , если два реберных графа связных графов изоморфны, то и графы изоморфны. Русопоулос (Roussopoulos)[12]использовал это наблюдение как базис для линейного по времени алгоритма распознавания реберных графов и реконструкции их исходных графов.

Например, такая характеристика может быть использована, чтобы показать, что следующий граф не является реберным:

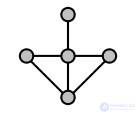
В этом примере ребра, идущие от центральной вершины 4-й степени вверх, влево и вправо не содержат общих клик. Так что любое разбиение ребер графа на клики должно содержать по меньшей мере одну клику для каждой из этих трех ребер, и все три клики пересекаются в центральной вершине, что нарушает условие, чтобы каждая вершина принадлежала в точности двум кликам. Таким образом, показанный граф не может быть реберным графом.

Другая характеристика графа была доказана Байнеке[13] (и была упомянута без доказательства ранее им же ). Он показал, что имеется девять минимальных графов, не являющихся реберными, таких, что любой граф, не являющийся реберным, содержит один из этих девяти графов в качестве порожденного подграфа. Таким образом, граф является реберным тогда и только тогда, когда никакое подмножество вершин не порождает один из этих девяти. В примере выше четыре верхних вершины порождают клешню (то есть, полный двудольный граф K1,3), показанный вверху слева иллюстрации запрещенных подграфов. Таким образом, по характеристике Байнеке, этот граф не может быть реберным. Для графов со степенью вершин не менее 5 только шесть подграфов в левом и правом столбцах рисунка могут порождаться графом[14]. Этот результат похож на результат для реберных графов гиперграфа.[15]

Повторение операции построения реберного графа

Руидж и Вильф[16] рассмотрели последовательность графов

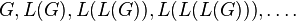
Они показали, что для конечного графа связного графа G возможны только четыре вида поведения этой последовательности:

• Если G — циклический граф, то L(G) и все последующие изоморфны самому графу G. Это единственное семейство связных графов, для которых L(G) изоморфноG.
• Если G — клешня K1,3, то L(G) и все последующие графы являются треугольниками.
• Если G — путь, то каждый последующий реберный граф — укороченный путь, пока он не превратится в пустой граф.
• Во всех остальных случаях размер графов увеличивается неограниченно.

Если G несвязен, то эта классификация применима к каждой отдельной компоненте связности графа G.

Связь с другими семействами графов

Любой реберный граф не содержит клешней.

Реберный граф двудольного графа является совершенным (смотри теорему Кенига). Реберные графы двудольных графов создают один из ключевых блоков, который используется для доказательства теоремы о совершенных графах. Специальным случаем являются ладейные графы, реберные графы полных двудольных графов.

Обобщения

Мультиграфы

Концепция реберного графа для графа G может быть естественным образом распространена на случай, когда G является мультиграфом, хотя, в этом случае, теорема Уитни о единственности становится неверной. Например, полный двудольный граф K1,n имеет тот же реберные граф, что и дипольный граф и мультиграф Шеннонас тем же числом ребер.

Реберные орграфы

Можно также обобщить реберные графы для ориентированных графов.[17]. Если G — ориентированный граф, то его ориентированный реберный граф или реберный орграф имеет одну вершину для каждой дуги из G. Две вершины, соответствующие дугам из u в v и из w в x из графа G связаны дугой из uv в wx в реберном орграфе, когда v = w. Таким образом, каждая дуга в реберном орграфе соответствует пути длиной 2 в исходном графе. Графы де Брейна могут быть получены путем многократного построения ориентированных реберных графов, начиная с полного орграфа[18].

Взвешеные реберные графы

Каждой вершине степени k в исходном графе G создает k(k-1)/2 ребер в реберном графе L(G). Для многих видов анализа это означает, что вершины высоких степеней в G представлены в сильнее в реберном графе L(G). Представим, например, случайное блуждание по вершинам исходного графа G. По ребру e мы пройдем с некоторой вероятностью f. С другой стороны, ребро e соответствует единственной вершине, скажем v, в реберном графе L(G). Если мы теперь осуществим тот же самый тип случайного блуждания по вершинам реберного графа, частота посещения v может оказаться совершенно отличной от f. Если наше ребро e в G было соединено с вершинами степени O(k), оно будет пройдено в O(k2) чаще в реберном графе L(G). Таким образом, хотя теорема Уитни[10] гарантирует, что реберный граф почти всегда содержит в себе закодированную топологию графа G, это не гарантирует, что эти два графа имеют простые динамические связи. Одно из решений этой проблемы — создать взвешенный реберный граф, то есть, реберный граф, у которого ребра снабжены весом. Имеется несколько естественных путей сделать это[19]. Например, если ребра d и e в графе G сопряжены в вершине v, имеющей степень k, то в реберном графе L(G) ребру, соединяющему две вершины d и e можно приписать вес 1/(k-1). Таким же образом любое ребро графа G (если только оно не соединено с вершиной степени '1') будет иметь вес 2 в реберном графе L(G), что соответствует двум концам ребра в G.

Реберные графы гиперграфов

Реберные графы гиперграфов

Ребра гиперграфа могут формировать любые семейства множеств, так что реберный граф гиперграфа — это то же самое, что и граф пересечений множеств семейства.

Вау!! 😲 Ты еще не читал? Это зря!

• блоковый граф , кликовое дерево , связанные классы графов ,

На этом все! Теперь вы знаете все про рёберный граф , Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое рёберный граф , производный граф, покрывающий граф и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.