Колесо (теория графов) кратко

Привет, сегодня поговорим про колесо теория графов , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое колесо теория графов , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

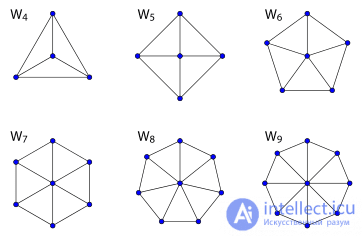
Примеры графов-колес
Вершин	n
Ребер	2(n − 1)
Диаметр	2 при n>4 1 при n=4
Обхват	3
Хроматическое число	3 при нечетном n, 4 при четном n
Свойства	гамильтонов двойственный планарный
Обозначение	Wn

В теории графов колесом Wn называется граф с n вершинами (n ≥ 4), образованный соединением единственной вершины со всеми вершинами (n-1)-цикла. Числовое обозначение колес в литературе не устоялось — некоторые авторы используют n для обозначения длины цикла, так что их Wn означает граф Wn+1по определению выше.[1] Колесо может быть определено также как 1-скелет[en] (n-1)-угольной пирамиды.

Предствление в виде множества

Пусть задано иножество вершин {1,2,3,…,v}. Об этом говорит сайт https://intellect.icu . Множество ребер графа-колеса можно представить в виде множества {{1,2},{1,3},…,{1,v},{2,3},{3,4},…,{v-1,v},{v,2}}.[2]

Свойства

Колеса являются планарными графами, а потому имеют единственное вложение в плоскость. Любое колесо является графом Халина. Они самодвойственны — двойственный граф любого колеса изоморфен самому колесу. Любой максимальный планарный граф, отличный от K4 = W4, содержит в качестве подграфа либо W5, либо W6.

В колесе всегда имеется гамильтонов цикл и число циклов в Wn равно 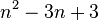(последовательностьA002061 в OEIS).

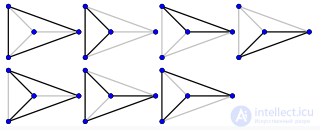
7 циклов в колесе W4.

Для нечетных значений n Wn является совершенным графом с хроматическим числом 3 — вершины цикла можно выкрасить в два цвета, а центральная вершина будет иметь третий цвет. Для четного n Wn колесо имеет хроматическое число 4 и (при n ≥ 6) не будет совершенным графом. W7 — это единственное колесо, являющеесяграфом единичных расстояний на евклидовой плоскости.[3]

Хроматический многочлен колеса Wn равен

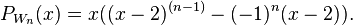
В теории матроидов есть два особо важных вида матроидов — колеса и вихри, и оба вида являются производными от графов-колес. матроид k-колеса — это графовый матроид колеса Wk+1, а матроид k-вихря получается из матроида k-колеса путем объявления внешнего цикла (обода) таким же независимым множеством, как и егоостовные деревья.

Колесо W6 дает контрпример гипотезе Пола Эрдеша в теории Рамсея — он высказал предположение, что полный граф имеет наименьшее число Рамсея среди всех графов с тем же хроматическим числом. Однако Фаудри и МакКей (Faudree, McKay, 1993) показали, что для W6 число Рамсея равно 17, в то время как для полного графа K4 с тем же хроматическим числом число Рамсея равно 18.[4] Таким образом, для любого графа G с 17 вершинами либо сам G, либо его дополнение содержитW6 как подграф, в то время как ни граф Пейли, имеющий 17 вершин, ни его дополнение не содержат K4.

Надеюсь, эта статья про колесо теория графов , была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое колесо теория графов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.