Элементы бинарной логики

Привет, сегодня поговорим про элементы бинарной логики, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое элементы бинарной логики , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

• Объекты бинарной логики

1. Некоторые логические функции
   Функции одной логической переменной (унарные)
   Функции двух логичеких переменных (бинарные)
2. Логические тождества
   Логические тождества с одной переменной
   Логические тождества с тремя переменными
   Тождества де Моргана
   Логические (булевы) базисы
3. Снтез комбинационных логических схем (функций)
   Определение формулы схемы (функции) по ее таблице истинности
   Минимизация логических функций с помощью аналитических преобразований
   Минимизация логических функций с помощью графического представления n-мерного куба
   Минимизация логических функций методом Куайна - Мак-Класки

• Литература

 

1. Объекты бинарной логики.

Бинарная (двоичная, математическая, формальная) логика в качестве объектов рассматривает логические утверждения (суждения, высказывания).

Любое утверждение в ее рамках может быть либо истинным (true), либо ложным (false), - "третьего не дано".

Условимся в первом случае присваивать утверждению значение "логической единицы", а во втором - "логического нуля".

Теперь любое утверждение можно рассматривать как некую "логическую переменную" со значениями 1 либо 0. Например, пусть утверждению "Жизнь на Земле существует" соответствует логическая переменная с именем x. Тогда x = 1 и т. д.

Для сложных комбинаций утверждений возможно определение функций (операций, действий) над логическими переменными. Таким образом, возникает "алгебра логики" или "булева алгебра" - по имени создателя такой алгебры английского математика и логика Буля (Bool) со своими действиями, свойствами и теоремами. Булева алгебра является логической базой цифровой техники.

Мы будем представлять логические функции одновременно в нескольких равноценных формах:

1. логическая формула: алгебраическая (аналитическая) форма;
2. диаграмма Венна: на некотором участке плоскости условно очерчена область, для точек которой данное утверждение истинно, - для остальных точек плоскости оно ложно; любой точке плоскости соответствует какое-то истинное утверждение, а любому "заведомо ложному" утверждению не соответствует ни одна точка;
3. таблица истинности: таблица состояний функции, в которой непосредственно указываются ее значения для всех возможных комбинаций значений логических переменных (всего в такой таблице 2n строк, где n - число логических переменных, 2 - число возможных состояний каждой переменной);
4. временнaя диаграмма: график зависимости состояния функции от времени, на котором каждая строка таблицы состояний отображается на некотором промежутке времени (такте) либо высоким (high) уровнем графика (логическая единица), либо низким (low) уровнем (логический нуль);
5. пространственная диаграмма: отображает таблицу истинности в декартовых координатах (до 4-х логических переменных);
6. логическая схема: состоит из "логических элементов", условно изображающих те или иные логические функции.

Для алгебраического представления логических функций, их таблиц истинности, временных диаграмм и логических схем будут использованы модели в Mathcad 2000, MS Excel 2000 и Electronics Workbench 5.12.

2. Некоторые логические функции.

2.1. Функции одной логической переменной (унарные).

Формально с любым утверждением можно либо согласиться, либо нет. Первому случаю соответствует функция "Логическое тождество (эквивалентность)".

Определим в Mathcad целочисленные переменные x, y и z, принимающие значения 0 либо 1. Определим также вышеназванную функцию переменной x как EQV(x):

 

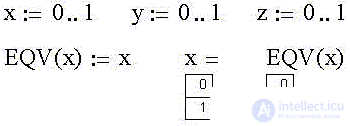
Определим теперь вторую из двух возможных унарную функцию "Логическое отрицание (НЕ, NOT, инверсия)" как NOT(x):

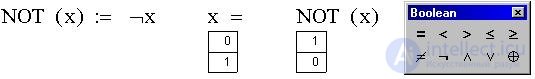
На рисунке приведена также панель логических (булевых) операторов Mathcad.

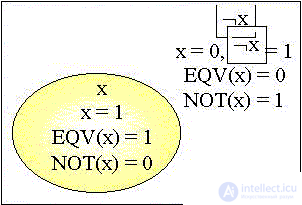
Начертим общую для двух функций диаграмму Венна:

Создадим в Excel таблицу истинности для функции логического отрицания:

Схемные изображения в Electronics Workbench логических элементов (Logic Gates) рассмотренных функций:

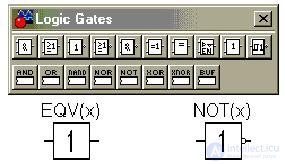
Второй элемент называется инвертором (обратим внимание на изображение инверсного выхода элемента). На рисунке приведена также панель логических элементов.

Построим в Electronics Workbench временную диаграмму на виртуальных моделях элементов, для чего входные значения получим из генератора слова (Word Generator), подав затем их и выходные значения на логический анализатор (Logic Analyzer):

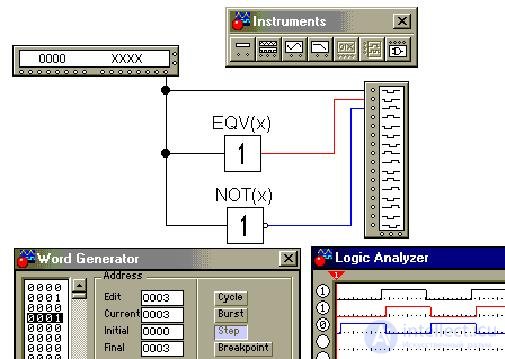
В шестнадцатиразрядном генераторе слова каждые 4 двоичные разряда (полубайт) кодируются шестнадцатеричной цифрой от 0 до F. В нашем случае, например, значению переменной x = 1 в генераторе соответствует двоичный код 0000 0000 0000 0001 и шестнадцатеричный код 0001, как на рисунке выше.

На рисунке приведена также панель инструментов (Instruments).

2.2. Функции двух логических переменных (бинарные).

Из более чем десятка таких функций рассмотрим только две: любая из них в комбинации с логическим отрицанием образует так называемый "логический базис", достаточный для синтеза остальных функций, а также произвольных логических автоматов.

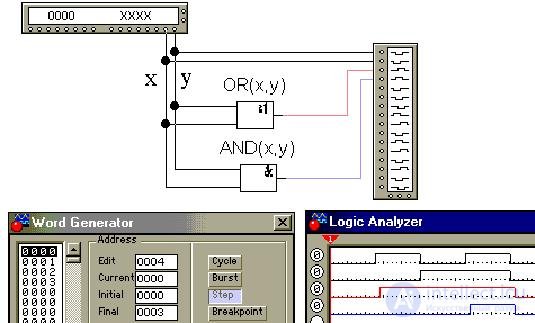
Определим бинарную функцию "Логическое сложение (ИЛИ, OR, дизъюнкция)" как OR(x):

Создадим соответствующую таблицу истинности в Excel:

Предположим, что переменной x соответствует утверждение "Мама купила рыбу", а переменной y - "Папа поймал рыбу", тогда их логической сумме, очевидно, соответствует утверждение "У кота Васьки сегодня на ужин рыбка!".

На диаграмме Венна последнее утверждение истинно на множестве точек, принадлежавшим либо x, либо y (площадь "восьмерки" - объединение x и y):

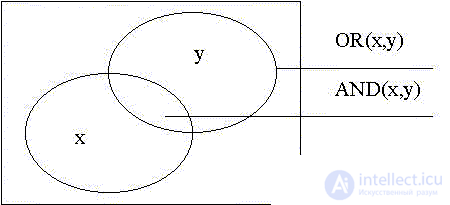
Но ситуация, когда x - это утверждение "Билет куплен", а y - "В кино не опоздали", дает только при одновременной истинности и одного, и другого истинность утверждения "Смотрим кинофильм". Последнее справедливо на множестве точек, принадлежавшим и x, и y на диаграмме Венна выше (площадь "листика" - пересечения x и y).

Определим такую бинарную функцию, - она называется "Логическое умножение (И, AND, конъюнкция)", - как AND(x):

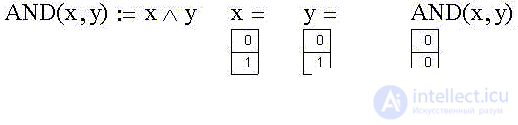
Создадим соответствующую таблицу истинности в Excel:

Получим временную диаграмму на виртуальных моделях дизъюнктора и конъюнктора, заметив, что в таблице выше в строках значений переменных сверху вниз идет двоичный счет от 00b = 0d = 0h до 11b = 3d = 3h (здесь: b - binary, двоичное, d - decimal, десятеричное и h - hexadecimal, шестнадцатеричное представления чисел):

3. Логические тождества.

3.1. Логические тождества с одной переменной.

Первое в ряду тождеств - результат двойного применения унарной операции отрицания к переменной - "закон отрицания отрицания": отрицание отрицания утверждения тождественно утверждению. Пример: утверждения "Я утверждаю" и "Я не не утверждаю" очевидно, эквивалентны.

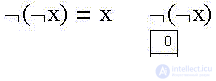
На диаграмме Венна первое отрицание переменной выводит за пределы области, где она истинна, второе отрицание возвращает в нее же, так как "третьей" возможности просто не существует.

Приведем доказательство в таблице Excel:

Следующая группа тождеств представляет результаты применения бинарных операций логической переменной с 0, с 1, с самой переменной и с ее отрицанием.

Если вспомнить, что на диаграмме Венна у заведомой лжи нулевая площадь, то, очевидно, что объединение с ней "не даст ничего нового", а пересечение с заведомой ложью имеет ее же нулевую площадь:

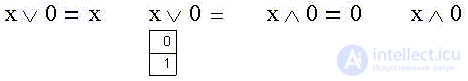
Объединение данного утверждения с любыми возможными истинными утверждениями совпадает с ними всеми, пересечение же со всеми возможными истинными утверждениями "вырезает" данное (в т. Об этом говорит сайт https://intellect.icu . ч., очевидно, и при его ложности):

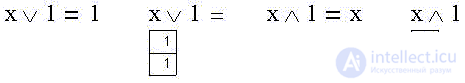
Очевидно также, что объединение и пересечение утверждения с самим собой эквивалентно самому утверждению (случай тавтологии):

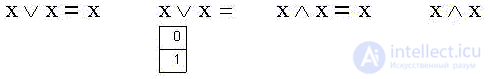
Наконец, истинна логическая сумма утверждения и его отрицания (одно из двух - истинно) так же, как ложно их произведение (их одновременная истинность):

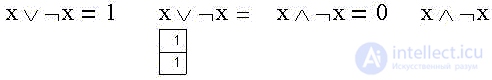
"Пациент скорее жив, чем мертв" (либо жив, либо не жив) - заведомая истина. И наоборот: "и жив, и не жив" - заведомая ложь.

3.2. Логические тождества с тремя переменными.

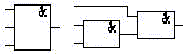
Примеры сочетательных (ассоциативных) свойств в алгебре логики:

На практике эти свойства позволяют заменить многовходовые логические элементы схем последовательно используемыми двухвходовыми, например:

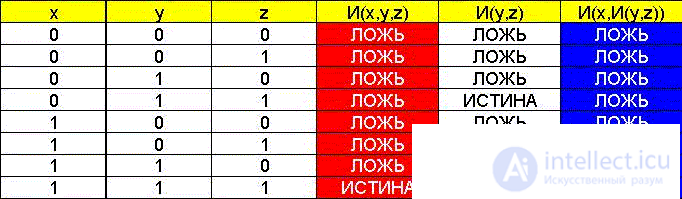
При доказательстве с помощью таблицы истинности появился отдельный столбец И(y,z), соответствующий действию в скобках:

Распределительные (дистрибутивные) свойства более интересны, - они показывают, что (в отличие от "обыкновенной" алгебры) операции логического сложения и умножения в формальной логике абсолютно симметричны: если в обеих частях тождества заменить дизъюнкцию конъюнкцией и наоборот, то опять получим тождество:

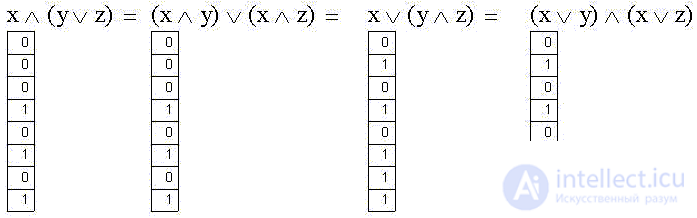
Речь идет о раскрытии скобок, причем, если обе части первого тождества в "обычных" алгебраических обозначениях имеют вполне привычный вид:

то второе тождество, которое получилось из симметричной замены в первом операций сложения на умножение и наоборот, выглядит весьма непривычно:

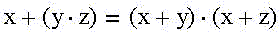
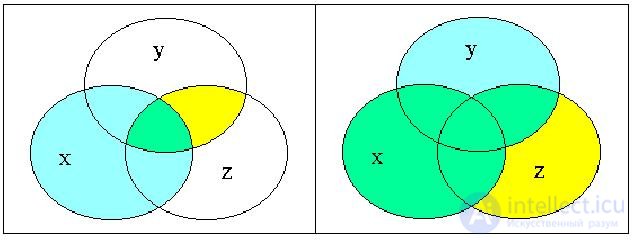
     Для наглядности представим левую и правую части этого тождества на отдельных диаграммах Венна:

3.3. Тождества де Моргана.

Практически наиболее интересна не симметричная замена сумм на произведения и наоборот, а именно либо замена только сумм на произведения, либо - только наоборот.

Соответствующие тождества носят название тождеств (правил) де Моргана (de Morgan). Рассмотрим случай двух переменных.

1) Отрицание логической суммы утверждений эквивалентно произведению их отрицаний:

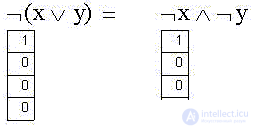
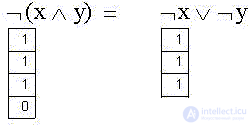
2) Отрицание логического произведения утверждений эквивалентно сумме их отрицаний:

Используя закон отрицания отрицания и вышеуказанные тождества, можно избавиться и от "чистых" сумм и произведений:

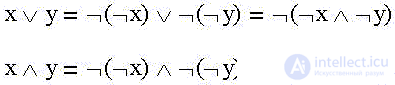
Приведем общую для четырех тождеств диаграмму Венна:

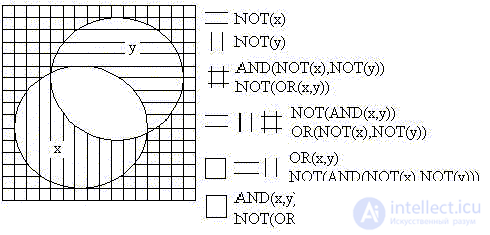
Покажем справедливость последнего тождества в Electronics Workbench:

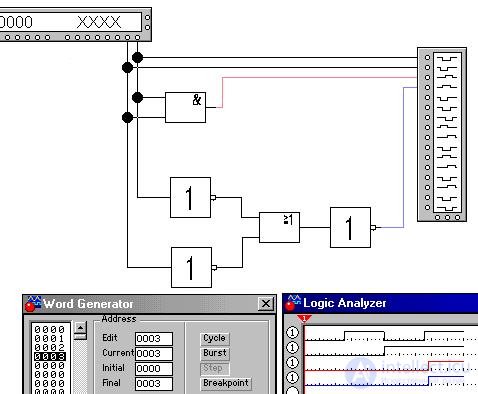
То же в Excel:

3.4. Логические (булевы) базисы.

Нетрудно показать, что объединение входов дизъюнктора с отрицанием или конъюнктора с отрицанием (левых частей тождеств де Моргана) дает инвертор, так что любая возможная логическая операция представима как комбинация логических комплексов 2-ИЛИ-НЕ, либо 2-И-НЕ, являющимися таким образом логическими базисами.

Покажем, например, правую часть только что рассмотренного тождества (замены логического произведения) в базисе "2-ИЛИ-НЕ", а левую часть, - само произведение, - в базисе "2-И-НЕ" (нижняя схема):

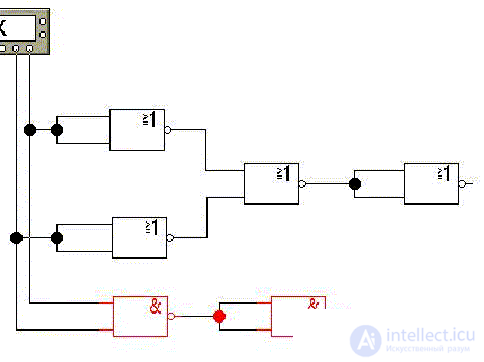
4. Синтез комбинационных логических схем (функций).

4.1. Определение формулы схемы (функции) по ее таблице истинности.

Представим себе в роли буриданова осла глупого кота Ваську, не способного выбрать между маминой и папиной рыбой и оставшегося без ужина:

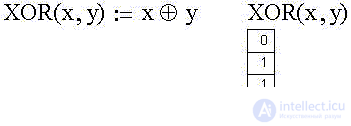
Функция XOR(x,y) называется "исключительное ИЛИ" (exclusive OR), а также "сумма по модулю 2" (сумма значений переменных х и у в младшем двоичном разряде).

Отобразим заданную таблицу истинности логической функции "Глупый кот Васька", в виде формулы - логической суммы произведений переменных (либо их отрицаний), для которых XOR(x,y) принимает значение логической единицы. Для этого добавим в таблицу столбцы значений всех возможных произведений и выберем нужные:

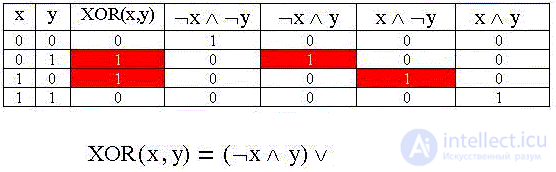
Полученная формула есть совершенная дизъюнктивная нормальная форма (СДНФ) логической функции, определенной таблицей истинности:

• "дизъюнктивная" как сумма произведений;
• "совершенная", поскольку в каждое произведение входят все переменные;
• "нормальная", так как в любом произведении каждая переменная встречается лишь однажды.

Приведенную выше таблицу можно представить и так:

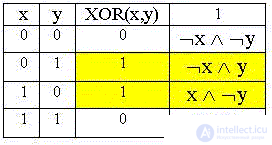
В четвертом столбце приведены произведения, равные логической единице для соответствующих значений переменных. В СДНФ входят произведения "рядом" с единицами определенного таблицей истинности логического автомата.

Определим в логическом конверторе (Logic Converter) таблицу истинности, соответствующую рассмотренной выше логической функции; получим для нее логическую формулу (СДНФ), логическую схему, а также схему в базисе 2-И-НЕ:

4.2. Минимизация логических функций с помощью аналитических преобразований.

Речь идет о том, чтобы перейти от СДНФ к ДНФ с минимумом слагаемых, при этом количество множителей в каждом слагаемом должно быть также минимальным (избавиться от "совершенства"). Иными словами - максимально уменьшить количество переменных и операций в СДНФ.

Упростить функцию можно непосредственно с помощью алгебраических преобразований с использованием вышерассмотренных тождеств (что не всегда просто при большом количестве переменных), а также путем преобразования таблицы состояний функции.

Рассмотрим оба варианта минимизации на примере функции трех логических переменных, заданной таблицей истинности ниже:

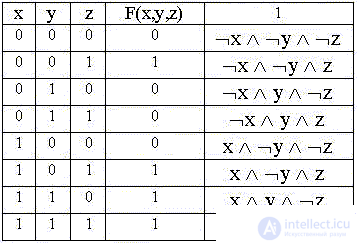
Запишем СДНФ:

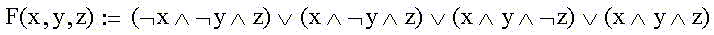
Сначала преобразуем правую часть "неудачно". Вынесем за скобки произведение x и z только из второй и четвертой слагаемых конъюнкций:

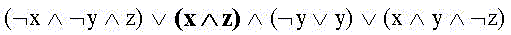
Воспользуемся уже известными тождествами:

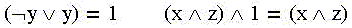
и получим далее не упрощаемую, "тупиковую" ДНФ (но не "минимальную"):

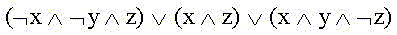
В ДНФ только три конъюнкции, причем во второй нет переменной y.

Теперь заметим, что в первой и второй конъюнкциях СДНФ можно вынести за скобки произведение отрицания y с z, а в третьей и четвертой - произведение x и y:

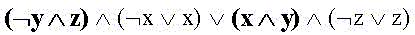
Воспользовавшись тождествами

получаем минимальную ДНФ:

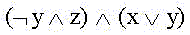
4.3. Минимизация логических функций с помощью графического представления n-мерного куба.

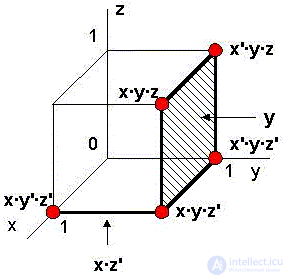
При количестве переменных не более 4-х все возможные тупиковые и саму минимальную формы можно просто увидеть на пространственной диаграмме - n-мерном (в нашем случае - 3-хмерном) кубе - декартовом графике, где на осях, соответствующих переменным, отображены точки их возможных состояний (0 или 1). Точки-состояния, в которых (согласно таблице истинности) функция принимает единичные значения, изобразим более крупными:

Штрих справа от имени переменной означает ее отрицание, для конъюнкции служит обычный знак умножения (как в логическом конверторе Electronics Workbench).

Формула ребра вдоль оси-переменной не содержит этой переменной, т. к. значение функции на "склеенных" им вершинах не зависит от значения этой переменной, что соответствует операции выноса за скобки общего множителя. Например, ребро x·z соединяет точки x·y'·z и x·y·z:

(x·y'·z) + (x·y·z) = x ·z ·(y' + y) = x ·z

По диаграмме задача минимизации сводится к объединению максимума вершин, на которых функция принимает единичные значения, в минимум ребер. В нашем случае - это два ребра y'·z и x·y, "склеившие" четыре вершины.

"Неудачный" вариант минимизации соответствует выбору одного ребра x·z и "оставшихся" вершин x'·y'·z и x·y·z'.

Очевидны другие тупиковые ДНФ: два варианта смежных ребер плюс одна оставшаяся вершины и три ребра. Все варианты не минимальны. Чтобы получить указанные варианты тупиковых форм аналитически, нужно воспользоваться известным тождеством

x + x = x

и записать "необходимую" конъюнкцию дважды. Например, по диаграмме очевидна ДНФ из двух ребер и точки:

F(x,y,z) = x·y + x·z + x'·y'·z

Получим ее аналитически, записав конъюнкцию x·y·z дважды (подчеркнуто):

F(x,y,z) = x'·y'·z + x·y'·z + x·y·z' + x·y·z + x·y·z = 
= x'·y'·z + x·y·(z' + z) + x·z ·(y' + y) =
= x'·y'·z + x·y + x·z

Заметим, что в случае, когда выделенные вершины образуют грань куба, формула такой грани состоит только из одной переменной (или ее отрицания), ось которой пересекает эта грань.

Пусть, например, дана СДНФ некоторой функции G(x,y,z):

G(x,y,z) = x·y'·z' + x·y·z + x'·y·z + x'·y·z' + x·y·z'

Здесь конъюнкции со 2-й по 5-ю как раз и образуют грань, формула которой - y:

Формула ребра, склеившего вершины x·y'·z' и x·y·z', есть x·z'. Так что минимальная ДНФ равна:

G(x,y,z) = x·z' + y

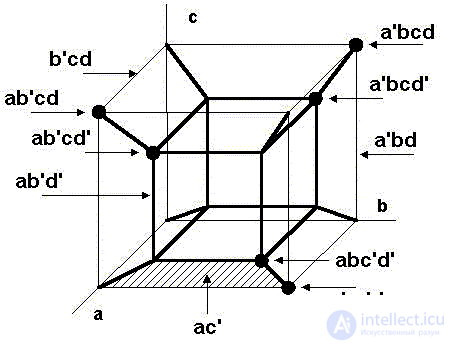
Пространственная диаграмма "выдерживает" представление и 4-й переменной, отрицание которой определяется на вершинахвнутреннего куба, вставленного во внешний куб. Значения других переменных определены на обоих кубах идентично:

4.4. Минимизация логических функций методом Куайна - Мак-Класки.

Вернемся теперь к функции F(x,y,z). Заметим, что объединение двух смежных вершин в ребро, соответствующее выносу за скобки общего множителя, в таблице истинности означает объединение двух строк в одну. В комбинируемых строках должны совпадать все значения переменных, кроме одной - сравниваемые строки отличаются на одну единицу. Значение "не совпавшей" переменной безразлично и может быть обозначено крестиком "x". Например, указанные ниже две строки (ребро y'·z)

можно заменить одной строкой:

т. к. в этой строке значение переменной x не влияет на единичность функции.

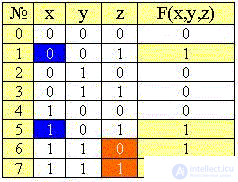
Минимизируем таблицу истинности нашей функции (см. ниже).

1. Удалим строки таблицы (№№ 0, 2, 3, 4), в которых F(x,y,z) принимает нулевые значения.
2. В оставшихся строках найдем пары строк, в которых одна и та же переменная принимает инверсные значения: №№ 1, 5 (переменная x) и №№ 6,7 (переменная z), а значения остальных переменных идентичны.
3. Объединим каждую пару строк в одну строку, как выше.

Можно ожидать, что СДНФ максимально свернутой таблицы истинности и будет минимальной ДНФ. Поэтому добавим в минимизированной таблице столбец конъюнкций "существенных" переменных.

=> 

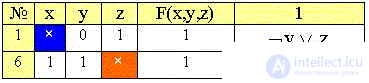
В последней таблице СДНФ совпала с минимальной ДНФ:

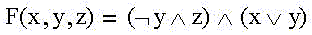
Получим тот же результат, последовательно шаг за шагом применяя общий метод Куайна - Мак-Класки (Quine - McCluskey) минимизации логических функций.

Шаг 1.

Запишем еще раз таблицу истинности для функции F(x,y,z) с указанием единичных конъюнкций-минтермов и количества единиц в значениях переменных:

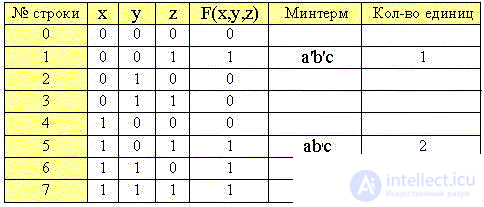
Шаг 2.

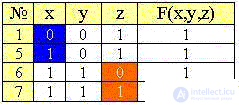
Разобьем таблицу на группы строк (минтермов) с одинаковым количеством единиц, удалив из таблицы строки с нулевым значением функции:

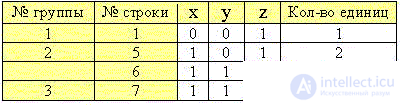
Шаг 3.

Сравним наборы значений переменных каждой предыдущей группы с последующей и объединим строки с общим множителем, как и ранее:

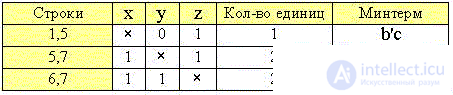
Шаг 4.

Убедимся в отсутствии минтермов с общими позициями "крестиков", т. е. в невозможности дальнейшего продолжения упрощения.

Шаг 5.

Заметим также, что получившаяся ДНФ не минимальна и соответствует трем ребрам на пространственной диаграмме:

F(x,y,z) = b'c + ac + ab.

Удалим поэтому из таблицы избыточную среднюю комбинацию из строк 5 и 7, так как строка 5 выше уже сгруппирована с 1-й, а строка 7 - ниже с 6-й. Получаем окончательную минимальную таблицу комбинаций строк и соответствующую ей минимальную ДНФ:

F(x,y,z) = b'c + ab.

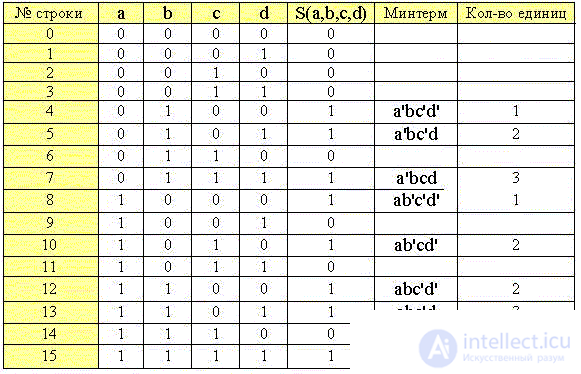
В качестве упражнения минимизируем функцию S(a,b,c,d) 4-х переменных, а результат дополнительно проверим в логическом конверторе Electronics Workbench (программа которого реализует алгоритм именно данного метода).

Саму же функцию S(a,b,c,d) зададим графически как "состоящую" из двух граней и отрезка. В таблице слева от чертежа указаны "координаты" крупных точек-вершин, на которых функция принимает единичные значения, или конъюнкции, входящие в СДНФ:

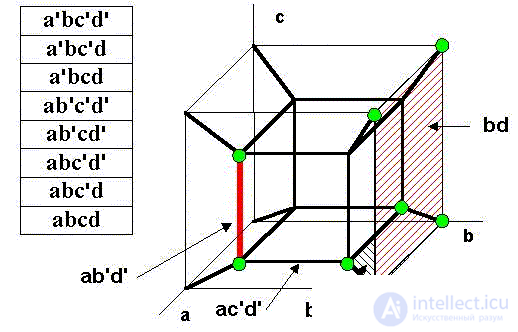
S(a,b,c,d) = a'bc'd' + a'bc'd + a'bcd + ab'c'd' + ab'cd' + abc'd' + abc'd + abcd

S(a,b,c,d) = ab'd' + bc' + bd

Для проверки в логическом конверторе перепишем правую часть СДНФ в верхнем регистре, прописными буквами:

A'BC'D'+A'BC'D+A'BCD+AB'C'D'+AB'CD'+ABC'D'+ABC'D+ABCD

скопируем и вставим в строку формулы конвертора:

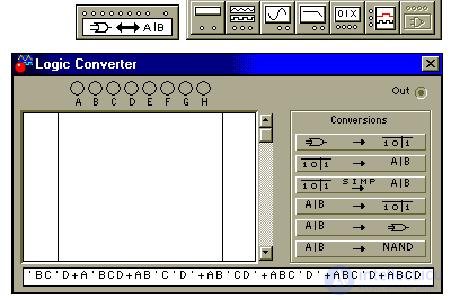
Теперь восстановим по формуле таблицу истинности (4-я кнопка) и упростим таблицу, получив в строке формулы минимальную ДНФ (3-я кнопка):

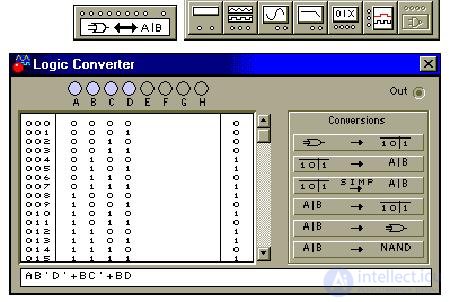
Минимизируем функцию S(a,b,c,d) методом Куайна - Мак-Класки.

1. Создадим таблицу истинности функции S(a,b,c,d):

2. Сгруппируем минтермы по количеству в них единиц:

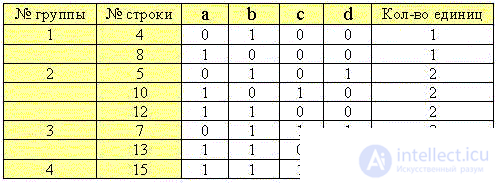
4. Произведем первое объединение строк каждых предыдущих и последующих групп:

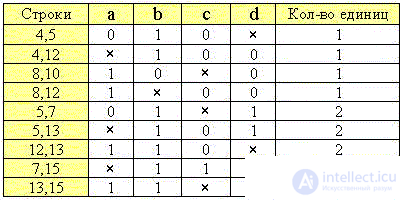
5. Объединим строки с совпадающими позициями "крестиков":

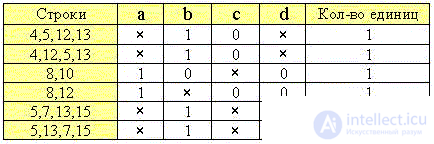
6. Из двух строк с идентичными значениями минтермов оставляем только одну:

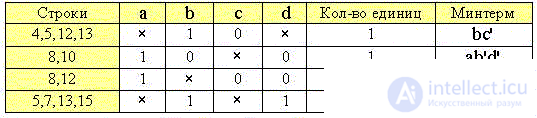
7. Обращаем внимание на то, что третий минтерм избыточен (лишнее ребро ac'd' на пространственной диаграмме), т. к. 8-я строка уже вошла в комбинацию с 10-й строкой (2-й минтерм), а 12-я - в комбинацию с 4-й, 5-й и 13-й строками (1-й минтерм). Поэтому удаляем третью строку таблицы и записываем минимальную СДНФ:

S(a,b,c,d) = bc' + ab'd' + bd.

Умение создавать и минимизировать логические функции имеет огромное значение при проектировании устройств цифровой электроники.

Литература:

1. Electronics Workbench. Professional Edition. User's guide. Version 5./Interactive Image Technologies Ltd. Canada. 1996
2. Electronics Workbench. Professional Edition. Technical Reference. Version 5./Interactive Image Technologies Ltd. Canada. 1996.
3. Потемкин И.С. Функциональные узлы цифровой автоматики./Энергоатомиздат, М., 1988.

На этом все! Теперь вы знаете все про элементы бинарной логики, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое элементы бинарной логики и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.